寻找素数

Kenneth Haugland

4.97/5 (65投票s)

2012年8月20日

CPOL

17分钟阅读

239138

3527

用代码解释不同的素数查找模式。

引言

寻找素数的方法有很多，网络上也有各种各样的应用。本文旨在收集一些最常见的方法并解释它们的原理。

背景

我将引用克雷数学研究所关于千禧年难题“黎曼猜想”的定义。

"有些数字具有特殊性质，不能表示为两个更小数的乘积，例如 2、3、5、7 等。这些数字被称为素数，它们在纯数学及其应用中都起着重要作用。"

这些数字一直是数学研究的热点，因为它们具有许多有趣的特性。最早研究这些问题的是古希腊人，他们基于欧几里得公理（尽管他生活在亚历山大，一个由亚历山大大帝建立的城市，大约在公元前 300 年）建立的证据和逻辑（大部分）至今仍然有效。这种构建一个始终有效的坚实参考的方法直到 20 世纪初库尔特·哥德尔的定理才被打破，尽管高斯和许多其他数学家在 19 世纪就遇到了公理的许多问题。

欧几里得可以说是第一个已知的素数研究来源，也是数论的第一个贡献。他证明了确实存在无限多个素数，并且用于《几何原本》的逻辑如下：

取任意有限个素数列表p₁、p₂、...、p_n。将证明存在至少一个不在该列表中的其他素数。设P为列表中所有素数的乘积：P = p₁p₂...p_n。设q = P + 1。那么，q要么是素数，要么不是：

如果q是素数，那么就存在比列表中更多的素数。

如果q不是素数，那么某个素因数p整除q。这个因数p不在我们的列表中：如果它在列表中，那么它就会整除P（因为P是列表中每个数的乘积）；但我们知道，p整除P + 1 = q。如果p整除P和q，那么p必须整除这两个数的差，即 (P + 1) - P，也就是 1。但没有素数能整除 1，所以这将产生矛盾，因此p不可能在列表中。这意味着列表中存在至少一个额外的素数。

这就证明了对于任何有限的素数列表，都存在一个不在列表中的素数。因此，素数必然是无限的。

他还提出了算术基本定理，该定理指出所有整数都可以表示为一或多个素数的乘积。

埃拉托斯特尼筛法

埃拉托斯特尼（公元前 276 年 - 公元前 195 年）是另一个对素数感兴趣的人，尤其对如何找到它们感兴趣（尽管我们并没有来自他那个时代的任何书面来源来证实这一点）。他提出了一种简单的筛分非素数的方法，为了实现这一点，我将把它分解为简单的编程步骤：

创建一个从 2 到 N 的布尔列表，并将所有项都填充为布尔值 True。
确定需要多少个筛子（这只是 N 的平方根）。
划掉列表中所有不是素数的数字。让我们从 2 开始，它是素数，那么 4、6、8 等就不是素数，并将对应的布尔值设为 false。

你可能会问：“为什么停在 Sqrt(N)？”答案是，两个数字能乘积的最大组合是 B*B = N。这意味着所有非素数都会有在 B 或 B 以下的因子。（你可以这里看到一个证明此点的严谨数学方法）。

埃拉托斯特尼筛法在维基百科的动画图片中得到了精彩展示：维基百科

下一步是实际实现算法，并用实际代码找到从 2 到 N 的所有素数。这可以如下进行（下载中的代码是不同的实现，只是速度有所不同。但它们都遵循与下面代码相同的步骤。我保留了文章中的代码，因为它比更快的代码更容易理解（或阅读）：

''' <summary>
''' Returns all the primes from 2 up to N
''' </summary>
''' <param name="N">Find all primes below N</param>
''' <returns></returns>
''' <remarks></remarks>
Private Function SieveOfEratosthenes(ByVal N As Integer) As List(Of Integer)
    'Stores all the prime numbers
    Dim result As New List(Of Integer)

    'We need an boolean array that indicates if the number is a prime
    Dim IsPrime As New List(Of Boolean)

    'Fill the array with all true values and we will start at the number 2
    For i As Integer = 0 To N - 2
        IsPrime.Add(True)
    Next

    'Find and store how many numbers we need to check
    Dim NumberOfPrimeChecks As Integer = CInt(Math.Sqrt(N))

    'Start checking at the number 2
    Dim CurrentNumber As Integer = 2

    'Loop through all the nessecary checks 
    For i As Integer = 0 To NumberOfPrimeChecks - 1
        If IsPrime(i) Then
            'if the number 2 is prime the number 4 is not etc...
            For j As Integer = i + CurrentNumber To IsPrime.Count - 1 Step CurrentNumber
                IsPrime(j) = False
            Next
        End If
        'Increments the counter
        CurrentNumber += 1
    Next

    'Print the stored result in our list based on the boolean values
    For i As Integer = 0 To IsPrime.Count - 1
        If IsPrime(i) Then
            result.Add(i + 2)
        End If
    Next

    Return result
End Function

这种筛法相当好，而且实际上相当快，那么有什么缺点呢？答案是所需的存储空间。

你实际上需要存储从 2 到 N 的所有布尔/位值，如果素数很大，这将是一个很大的列表（在 .NET 中，Boolean并不总是 RAM 中的一个位，因此你可能可以通过在 C++ 中结合简单的指针使用位/字节作为存储来最小化存储）。总结结果：

速度	N ln ln N + O(N)
存储	N

这意味着如果你想对更大的素数使用我展示的算法，则需要对其进行修改。我们设计了一种新算法，该算法在知道 M 以下的所有素数的情况下，可以找到 M 到 N 之间的素数。该算法如下：

''' <summary>
''' Gives out all the primes from 2 to N, given the primes below M and the start finding new primes at M
''' </summary>
''' <param name="M">Start the check fore new primes at M</param>
''' <param name="N">The upper boundary for finding primes N</param>
''' <param name="PiPrime">All the primes below M, includeed M</param>
''' <returns>A list of primes from 2 to N</returns>
''' <remarks>This function requires that you have all the prime numbers below M</remarks>
Private Function SieveOfEratosthenes(ByVal M As Integer, ByVal N As Integer, _
                 ByVal PiPrime As List(Of Integer)) As List(Of Integer)
    'Stores all the prime numbers
    Dim result As New List(Of Integer)
    result = PiPrime
    'We still have to do Sieveing with the lowest prime numbers 
    Dim HigestModPi As New List(Of Integer)
    For i As Integer = 0 To PiPrime.Count - 1
        Dim temp As Integer = CInt(Math.Ceiling(M / PiPrime(i))) * PiPrime(i)

        HigestModPi.Add(temp)

    Next

    'We need an boolean array that indicates if the number is a prime
    Dim IsPrime As New List(Of Boolean)

    'Fill the array with all true values and we will start at the number 2
    For i As Integer = M To N - 1
        IsPrime.Add(True)
    Next
 
    'Find and store how many numbers we need to check
    Dim PrimeCheckStop As Integer = CInt(Math.Sqrt(N))

    For i As Integer = 0 To PiPrime.Count - 1
        If PiPrime(i) > PrimeCheckStop Then
            Exit For
        End If

        For j As Integer = 0 To IsPrime.Count - 1 Step PiPrime(i)
            Dim h As Integer = HigestModPi(i) - M + j
            IsPrime(h) = False
        Next
    Next

    'Check if we have performed all checks fo rthe possible primes primes between M and N
    If M < Math.Sqrt(N) Then
        For i As Integer = M To PrimeCheckStop
            If IsPrime(i) Then
                For j As Integer = i * 2 To N Step i
                    IsPrime(j) = False
                Next
            End If
        Next
    End If

    For k As Integer = 0 To IsPrime.Count - 1
        If IsPrime(k) Then
            result.Add(M + k)
        End If
    Next

    Return result
End Function

在速度方面，结果是相同的，但由于我们没有无限的 RAM，因此这是一种获取几乎所有所需素数的实用方法。该算法的具体细节如下：

速度	(N-M) ln ln (N-M) + O(N-M)
存储	N-M + 素数

如果你想知道如何找到最佳的范围，那将非常棘手，因为它将取决于你的 RAM 容量。无论如何，在某个时候，你将被迫检查没有素数的数字范围，并且随着数字越来越高，你最终将不得不停止，因为某些素数（因为它们无限存在）肯定会大于你能存储在计算机上的数字。但我至少可以告诉你，根据贝尔特兰猜想（由切比雪夫证明）的论述，你肯定能在 N 和 2*N 之间找到一个素数。

然而，不可能在数组中包含超过 Integer.MaxValue 个元素，但你计算机的本地内存通常是瓶颈。

打破数学的“黑暗时代”

我将要展示的下一个算法直到 1999 年才被发现，并于 2004 年首次发表。为了解释它是如何工作的，我将回顾理解该算法工作原理所需的、与素数研究最相关的历史。

古希腊文明衰落后，直到 17 世纪才出现了关于纯数论的已知研究。最终打破这一僵局的人之一是费马，他是在业余时间作为爱好进行的，尽管他与另一位伟大的法国数学家帕斯卡进行了大量交流。他提出了著名的费马小定理：

a^p-1 = 1 (mod p)，其中 a < p

例如，如果 a = 2 且 p = 7，则 2⁶ = 64，而 64 - 1 = 63 = 7 × 9。余数（或更确切地说，模 7 的数）是 1/7。这可以用几种不同的方式书写，但通用的方程和结果总是相同的。

在此之后，涌现了许多杰出的数学家，其中有五位对现代计算机时代之前的素数发展产生了巨大影响：欧拉、切比雪夫、拉格朗日、高斯和黎曼。

欧拉还设计了第一个生成素数的_多项式_，我将其作为一项趣味知识列出。其他例子可以在这里看到：

P(x)= x²-x + 41

p(40) = 1601

从 0 到 40 的所有值都会产生素数，而 p(40) 到 p(80) 的值会生成 33 个素数。如果我们扩展到 p(1000)，58% 的数字是素数，而在该范围内的算术级数中只有 7% 是素数。威廉·邓纳姆（William Dunham）有一个精彩的视频，解释了欧拉的一些研究，可以在这里观看。

欧拉也是第一个发展了现在可以说是黎曼 Zeta 函数_基础_公式的人。但一如既往，欧拉还提供了另一个关于素数的有趣事实（该方程的完整推导可以在这里看到，它实际上是埃拉托斯特尼筛法的一个数学版本）。其壮观的结果是：

展开级数后：

和

欧拉还发展了模运算的第一个现代应用，这意味着模数同余。这是费马小定理的进一步发展和形式化，通常被解释为时钟算术。现代解释的方法可以在维基百科或MathWorld上查看，当今的语法是从拉格朗日开始的。

下一个数学家高斯（拉格朗日的同时代人）扩展了我们今天所知的收敛模。但我们将从高斯和素数之间的距离问题开始，或者更确切地说，在一组从 2 到 N 的数字中，击中一个素数的概率是多少？嗯，答案可以通过下表显示，其中 N 是从 1 到 N 的整数，Pi(N) 是小于 N 的素数个数，小于 N 的素数概率是 1/P(N)：

N	Pi(N)	P(N) = N/Pi(N)
10	4	2.5
100	25	4.0
1000	168	6.0
10000	1,229	8.1
100000	9,592	10.4
1000000	78,498	12.7
10000000	664,579	15.0
100000000	5,761,455	17.4

小表显示了自然对数 10 的增加，ln(10) = 2.3，这意味着每次算术级数乘以 10 时，（1/概率）平均增加 2.3 倍。然而，这个函数可以稍作修改，得到一个积分表示，给出 Li(x) 函数。

如果我们将积分展开成泰勒级数，当 x 趋于无穷时，下面级数中的第一项就是高斯在 15 岁时推导出的！

最重要的事情是认识到同余模的发展是如何形成了我们今天最常用的下一个算法（用于快速实现）。同余的通用公式是：

我为什么要告诉你这些？好吧，那是因为我接下来要展示代码的算法使用了同余的研究来生成素数。

数学王子高斯也请黎曼研究实部和虚部在图上绘制的应用。结果和广义模式最终将导致黎曼 Zeta 函数，其中所有非平凡零点都位于黎曼 Zeta 函数的实轴上。

实部与虚部绘图在某种意义上与收敛模相同。当我们用虚数 i (1i) 乘以一个实数时，这相当于将角度旋转 90 度。通过令 s= a + it 来找到素数函数的零点，或者黎曼推测所有非平凡零点（t=0 不计），他推测所有零点都位于 s = 1/2+it。

计算这些零点实际上非常复杂，因为它涉及一些复数算术。它通常涉及在复平面上进行积分（称为梅林积分），并使用黎曼-西格尔公式。这是一个相当复杂的故事，但你可以在奥德利兹科的页面上找到一些解释（请注意，它涉及 FFT 算法和许多复杂的数学主题，奥德利兹科还拥有关于零点分布的尚未被证明的定理）。

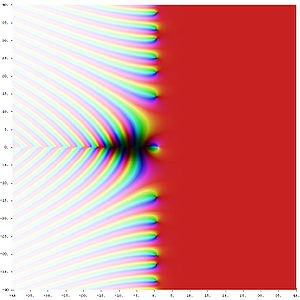
下图显示了黎曼 Zeta 函数，临界线可以在这里看到，其中实部等于 1/2（红色部分从 1/2 开始）。

还有一个称为乌拉姆螺旋的好奇事物，以其发明者斯坦尼斯瓦夫·乌拉姆的名字命名，他于 1963 年发现了它。乌拉姆螺旋用于创建素数的简单可视化，揭示了某些二次多项式生成异常多素数的明显趋势。它是在一次科学会议上展示一篇“冗长而非常乏味的论文”时发现的。它是通过将数字写成螺旋形创建的，如下图所示，你可以在维基百科上阅读更多相关信息。

螺旋线可以通过球体可视化，球体越大表示该数字可以分解的因子越多。下图显示了乌拉姆螺旋，图片来自此网站。

素数被认为是随机的或几乎随机的，这使得很难从中找到任何模式。如果你看看埃拉托斯特尼筛法，你已经看到了我们可以轻松地找到非素数的模式，但只有在排除了所有其他模式后才能找到素数。

自然界中也有素数随机性的证据。在自然界中，进化特征是，如果一个物种寻求随机性，你通常会发现素数在起作用。黎曼方程也是如此，其中误差项与随机波动一致。

这个故事还表明，为了找到素数的模式，我们通常将它们视觉化地转换为某种形式的螺旋形或圆形自然数串。几乎所有从同余模、乌拉姆螺旋以及黎曼 Zeta 函数中的复数和黎曼零点进行的计算似乎都与这个事实有关。

阿特金筛法

阿特金筛法（由 A.O.L. Atkin 和 Daniel J. Bernstein 于 2004 年创建）实际上与埃拉托斯特尼筛法正好相反，它标记素数而不是非素数。有关其推导的详细说明，请参阅创作者撰写的这篇文章此处。该筛法可以分解为以下步骤（来自维基百科）：

所有余数都以模六十为基数（将数字除以六十并返回余数）。
所有数字，包括 x 和 y，都是正整数。
翻转筛列表中的一个条目意味着将标记（素数或非素数）更改为相反的标记。
创建一个结果列表，填充 2、3 和 5。
创建一个筛列表，其中包含每个正整数的条目；此列表中的所有条目最初都应标记为非素数。
对于筛列表中的每个条目号 n，模六十余数为 r
如果 r 是 1、13、17、29、37、41、49 或 53，则翻转 4x² + y² = n 的每个可能解的条目。
如果 r 是 7、19、31 或 43，则翻转 3x² + y² = n 的每个可能解的条目。
如果 r 是 11、23、47 或 59，则在 x > y 的情况下，翻转 3x² - y² = n 的每个可能解的条目。
如果 r 是其他任何值，则完全忽略它。

从筛列表中的最小数字开始。
取筛列表中下一个仍标记为素数的数字。
将该数字包含在结果列表中。
将该数字平方并将其所有倍数标记为非素数。
重复步骤 5 到 8。
这导致具有奇数个解的数字为素数，具有偶数个解的数字为非素数。

代码几乎是从这里的伪代码转换而来（尽管看到 Torleif Berger 在这里实现的 C# 版本非常有帮助，代码几乎是精确复制，只是在本文中转换成了 VB）。请注意，下面的代码实际上比下面代码所示的埃拉托斯特尼筛法慢得多。主要原因是每个二次方程都必须执行复杂的计算和测试。代码仅用于说明其原理，如果您真的想实现一个快速的阿特金筛法，您应该使用（或修改）可以此处下载的 C 代码。实现速度更快是因为程序中存储了预先计算的表。这可能有点令人失望，因为该算法本质上是一个非常好的素数压缩文件。

''' <summary>
''' Returns a list of Primes from 2 to N
''' </summary>
''' <param name="N">Find prime numbers equal or lower than N</param>
''' <returns>List of primes as List(of BigInteger)</returns>
''' <remarks>For large primes you can get out of memory exceptions</remarks>
Private Function SieveOfAtkin(ByVal N As System.Numerics.BigInteger) As List(Of System.Numerics.BigInteger)
    Dim primes As New List(Of System.Numerics.BigInteger)

    Dim isPrime = New Boolean(N) {}
    Dim sqrt As System.Numerics.BigInteger = Math.Sqrt(N)

    For x As System.Numerics.BigInteger = 1 To sqrt
        For y As System.Numerics.BigInteger = 1 To sqrt
            Dim n1 = 4 * x * x + y * y
            If n1 <= N AndAlso (n1 Mod 12 = 1 OrElse n1 Mod 12 = 5) Then
                isPrime(n1) = isPrime(n1) Xor True
            End If

            n1 = 3 * x * x + y * y
            If n1 <= N AndAlso n1 Mod 12 = 7 Then
                isPrime(n1) = isPrime(n1) Xor True
            End If

            n1 = 3 * x * x - y * y
            If x > y AndAlso n1 <= N AndAlso n1 Mod 12 = 11 Then
                isPrime(n1) = isPrime(n1) Xor True
            End If
        Next
    Next

    For n2 As System.Numerics.BigInteger = 5 To sqrt
        If isPrime(n2) Then
            Dim s = n2 * n2
            Dim k As System.Numerics.BigInteger = s
            While k <= N
                isPrime(k) = False
                k += s
            End While
        End If
    Next

    primes.Add(2)
    primes.Add(3)
    For n3 As System.Numerics.BigInteger = 5 To N Step 2
        If isPrime(n3) Then
            primes.Add(n3)
        End If
    Next
    Return primes
End Function

该算法的具体结果如下，我们看到了巨大的改进，尤其是在素数变大时。然而，对于一小部分素数，差异并不巨大：

速度	N/log log N
存储	N^{1/2 + o(1)}

我们现在看到速度有所提高，存储需求也大不相同，尽管它比埃拉托斯特尼筛法要难实现得多。

历史

本文汇集了散布在网络上的零散信息，如果我忘记包含应包含的任何引用，请接受我最诚挚的歉意。撰写本文的目的是展示用于获取素数的筛法，并简要概述一些素数的性质以及尚未解决的问题。

现在您应该拥有一个出色的寻找素数的工具箱了，您可以直接前往Project Euler网站开始解决问题。您甚至可以开始考虑破解加密的消息，但您不应忘记泰伦斯·陶的话，即尚未从数学上证明，如果您能找到一个快速分解数字的公式，您就能破解加密消息。

C# 和 VB 下载中的代码已更改，这得益于 Clifford Nelson 发布的替代方案。然而，我没有更改文章中的代码，因为下载基本上使用了相同的步骤，只是重新排列了一下。它还大大加快了实现速度，因为它利用了数组而不是列表。

参考文献

我作为主要来源使用的书写于 2001 年，比阿特金筛法发表早三年，因此缺少对近期发现的解释。但是，它仍然提供了许多相关材料，并且还描述了素数在现实世界场景中的许多实际应用。

"素数 - 计算视角", 2001, Richard Cramdall 和 Carl Pomerance, Springer

"素数的音乐", 2004, Marcus Du Sautoy, Harper Perennial

关于阿特金筛法的源代码和文章：

其他筛法：

YouTube 上 David Metzler 的关于黎曼猜想的优秀视频系列（即使您只懂基础数学也很有用）：

Richard Taylor 关于模数同余和其他素数方面的讲座

素数与方程

以及 Marcus Du Sautoy 的视频演示

素数的音乐

CodeProject 网站上关于该主题的在线链接：