寻找素数

Kenneth Haugland

4.97/5 (65投票s)

2012年8月20日

CPOL

17分钟阅读

239135

3527

用代码解释不同的素数查找模式。

引言

网络上有许多关于查找素数及其使用方法的方案。本文旨在收集一些最常见的方法并解释它们的工作原理。

背景

我将从克雷数学研究所的素数定义中引用，该定义来自关于黎曼猜想的千禧年问题。

“有些数字具有特殊属性，即它们不能表示为两个较小数的乘积，例如2、3、5、7等。这些数字称为素数，它们在纯数学及其应用中都起着重要作用。”

这些数字一直是数学界深入研究的对象，因为它们具有许多有趣的性质。最早研究这些问题的是古希腊人，他们基于欧几里得公理（尽管他生活在大约公元前300年的亚历山大城，这座城市由亚历山大大帝建立）建立的证据和逻辑（在很大程度上）至今仍然有效。直到20世纪初哥德尔的定理出现，这种构建一个始终有效的可靠参考的方法才被打破，尽管高斯和许多其他数学家在19世纪就遇到了公理的许多问题。

欧几里得可以被认为是第一个已知的素数研究来源，也是纯数论的第一个贡献。他证明了确实存在无限多个素数，其《几何原本》中使用的逻辑如下：

取任意有限个素数列表p₁, p₂, ..., p_n。将证明至少存在一个不在该列表中的额外素数。设P为列表中所有素数的乘积：P = p₁p₂...p_n。设q = P + 1。那么，q要么是素数，要么不是：

如果q是素数，那么存在的素数比列表中列出的要多一个。

如果q不是素数，那么某个素数因子p整除q。这个因子p不在我们的列表中：如果它在列表中，那么它将整除P（因为P是列表中每个数的乘积）；但正如我们所知，p整除P + 1 = q。如果p整除P和q，那么p必须整除这两个数的差，即（P + 1） - P，也就是1。但没有任何素数能整除1，所以会产生矛盾，因此p不能在列表中。这意味着列表中存在的素数比列表中的多至少一个。

这证明了对于任何有限的素数列表，都存在一个不在列表中的素数。因此，必然存在无限多个素数。

他还提出了算术基本定理，该定理指出所有整数都可以表示为一次或多次素数的乘积。

埃拉托斯特尼筛法

埃拉托斯特尼（公元前276年 - 公元前195年）是另一位对素数感兴趣的人，尤其是如何找到它们（尽管我们没有他那个时代的书面资料来证实这一点）。他提出了一种简单的筛除非素数的方法，为了实现这一点，我将把它分解为简单的编程步骤：

创建一个从2到N的布尔列表，并将所有元素填充为布尔值True。
确定需要多少个筛子（这只是N的平方根）。
划掉列表中不是素数的所有数字。让我们从2开始，2是一个素数，数字4、6、8等不是素数，您将对应的布尔值设置为false。

您可能会问：“为什么停在Sqrt(N)？”答案是，两个数字相乘能得到的最大组合是B*B = N。这意味着所有非素数都有在B或B以下的因子。（您可以在这里看到一个证明这个的严格数学方法）。

埃拉托斯特尼的筛法在维基百科的动画图中得到了精美的展示：

下一步是实际实现该算法，并在实际代码中找到从2到N的所有素数。可以这样做（下载中的代码是不同的实现，只是速度不同。它们都经过相同的步骤，与下面的代码相同。我将下面的代码保留在文章中，因为它比更快的代码更容易理解（或阅读）：

''' <summary>
''' Returns all the primes from 2 up to N
''' </summary>
''' <param name="N">Find all primes below N</param>
''' <returns></returns>
''' <remarks></remarks>
Private Function SieveOfEratosthenes(ByVal N As Integer) As List(Of Integer)
    'Stores all the prime numbers
    Dim result As New List(Of Integer)

    'We need an boolean array that indicates if the number is a prime
    Dim IsPrime As New List(Of Boolean)

    'Fill the array with all true values and we will start at the number 2
    For i As Integer = 0 To N - 2
        IsPrime.Add(True)
    Next

    'Find and store how many numbers we need to check
    Dim NumberOfPrimeChecks As Integer = CInt(Math.Sqrt(N))

    'Start checking at the number 2
    Dim CurrentNumber As Integer = 2

    'Loop through all the nessecary checks 
    For i As Integer = 0 To NumberOfPrimeChecks - 1
        If IsPrime(i) Then
            'if the number 2 is prime the number 4 is not etc...
            For j As Integer = i + CurrentNumber To IsPrime.Count - 1 Step CurrentNumber
                IsPrime(j) = False
            Next
        End If
        'Increments the counter
        CurrentNumber += 1
    Next

    'Print the stored result in our list based on the boolean values
    For i As Integer = 0 To IsPrime.Count - 1
        If IsPrime(i) Then
            result.Add(i + 2)
        End If
    Next

    Return result
End Function

这种筛法非常好，而且实际上相当快，那么有什么问题呢？答案是所需的存储空间。

您实际上需要存储从2到N的所有布尔/位值，如果素数很大，这将是一个相当大的列表（在.NET中，布尔值并不总是RAM中的一个位，因此您可以通过结合使用位/字节存储和简单的指针来在C++中最小化存储）。总结结果：

速度	N ln ln N + O(N)
存储	N

这意味着，如果您想将其用于更大的素数，我向您展示的算法必须进行修改。我们设计了一个新算法，该算法在知道M以下所有素数的情况下，找到M到N之间的素数。该算法如下：

''' <summary>
''' Gives out all the primes from 2 to N, given the primes below M and the start finding new primes at M
''' </summary>
''' <param name="M">Start the check fore new primes at M</param>
''' <param name="N">The upper boundary for finding primes N</param>
''' <param name="PiPrime">All the primes below M, includeed M</param>
''' <returns>A list of primes from 2 to N</returns>
''' <remarks>This function requires that you have all the prime numbers below M</remarks>
Private Function SieveOfEratosthenes(ByVal M As Integer, ByVal N As Integer, _
                 ByVal PiPrime As List(Of Integer)) As List(Of Integer)
    'Stores all the prime numbers
    Dim result As New List(Of Integer)
    result = PiPrime
    'We still have to do Sieveing with the lowest prime numbers 
    Dim HigestModPi As New List(Of Integer)
    For i As Integer = 0 To PiPrime.Count - 1
        Dim temp As Integer = CInt(Math.Ceiling(M / PiPrime(i))) * PiPrime(i)

        HigestModPi.Add(temp)

    Next

    'We need an boolean array that indicates if the number is a prime
    Dim IsPrime As New List(Of Boolean)

    'Fill the array with all true values and we will start at the number 2
    For i As Integer = M To N - 1
        IsPrime.Add(True)
    Next
 
    'Find and store how many numbers we need to check
    Dim PrimeCheckStop As Integer = CInt(Math.Sqrt(N))

    For i As Integer = 0 To PiPrime.Count - 1
        If PiPrime(i) > PrimeCheckStop Then
            Exit For
        End If

        For j As Integer = 0 To IsPrime.Count - 1 Step PiPrime(i)
            Dim h As Integer = HigestModPi(i) - M + j
            IsPrime(h) = False
        Next
    Next

    'Check if we have performed all checks fo rthe possible primes primes between M and N
    If M < Math.Sqrt(N) Then
        For i As Integer = M To PrimeCheckStop
            If IsPrime(i) Then
                For j As Integer = i * 2 To N Step i
                    IsPrime(j) = False
                Next
            End If
        Next
    End If

    For k As Integer = 0 To IsPrime.Count - 1
        If IsPrime(k) Then
            result.Add(M + k)
        End If
    Next

    Return result
End Function

在速度方面，结果相同，但由于我们没有无限的RAM，因此这是一种获取几乎所有所需素数的实用方法。该算法的具体细节如下。

速度	(N-M) ln ln (N-M) + O(N-M)
存储	N-M + Primes

如果您想知道如何找到最优的范围，那将非常棘手，因为它将取决于您的RAM功能。无论如何，您最终都会被迫检查不包含素数的数字范围，并且随着数字的不断增大，您最终必须停止，因为由于素数是无限的，它们必然会大于您计算机上可以存储的数字。但至少我可以肯定地说，根据切比雪夫的证明，您保证能在N和2*N之间找到一个素数。

然而，数组最多只能包含Integer.MaxValue个项目，但您计算机的本地内存通常是瓶颈。

打破数学的“黑暗时代”

我将要展示的下一个算法直到1999年才被发现，并于2004年首次发表。为了解释它的工作原理，我将回顾理解该算法所需的最相关的素数研究历史。

古希腊文明衰落后，直到17世纪，没有已知的纯数论研究。终于打破这一僵局的人之一是费马，他是在业余时间作为爱好进行的，尽管他与另一位伟大的法国数学家帕斯卡进行了大量交流。他提出了以下公式，该公式被称为费马小定理：

a^p-1 = 1 (mod p)，其中a < p

例如，如果a = 2且p = 7，则2⁶ = 64，且64 - 1 = 63 = 7 × 9。余数（或者说模7的数）是1/7。这可以用几种不同的方式表示，但通用的方程和结果始终相同。

此后，涌现了许多杰出的数学家，其中有五位对计算机时代之前的素数发展产生了巨大影响：欧拉、切比雪夫、拉格朗日、高斯和黎曼。

欧拉还设计了第一个素数生成多项式，我在下面将其作为一种有趣的现象列出。其他示例可以在这里查看：

P(x)= x²-x + 41

p(40) = 1601

从0到40的所有值都能生成素数，而p(40)到p(80)的值生成33个素数。如果我们进一步到p(1000)，58%的数字是素数，而在该范围内的算术级数中只有7%是素数。威廉·邓纳姆（William Dunham）有一个关于欧拉研究的精彩视频可以在这里观看。

欧拉也是第一个开发出如今可以说是黎曼Zeta函数基本构建块公式的人。但与往常一样，欧拉还提供了另一个关于素数的有趣事实（该方程的完整推导可以在这里找到，它实际上是埃拉托斯特尼筛法的数学版本）。令人惊叹的结果如下：

写出级数：

和

欧拉还开发了现代模运算的第一个应用，即模某个数的同余。这是费马小定理的进一步发展和形式化，通常解释为时钟算术。今天的方法的现代解释可以从维基百科或MathWorld查看，今天的语法始于拉格朗日。

接下来的数学家高斯（拉格朗日的同代人）扩展了我们今天所知的收敛模。但我们将从高斯开始，探讨素数有多接近，或者说，在一个2到N的数字集合中，选中的数字是素数的概率是多少？嗯，答案可以通过下表显示，其中N是1到N的整数，Pi(N)是小于N的素数数量，小于N的素数概率是1/P(N)：

N	Pi(N)	P(N) = N/Pi(N)
10	4	2.5
100	25	4.0
1000	168	6.0
10000	1,229	8.1
100000	9,592	10.4
1000000	78,498	12.7
10000000	664,579	15.0
100000000	5,761,455	17.4

这个小表显示了自然对数10的对数增加，ln(10) = 2.3，这意味着每次算术级数乘以10，（1/概率）平均增加2.3倍。然而，这个函数可以稍微修改成一个积分表示，得到Li(x)函数。

如果将积分展开成当x趋于无穷时的泰勒级数，则以下级数中的第一项是高斯在15岁时就推导出的！

最重要的一点是，同余模的发展是如何形成今天最常用的算法（用于快速实现）的。同余的通用形式如下：

我为什么告诉你这些，因为我接下来要展示的代码使用的就是同余研究来生成素数的。

还是高斯，这位数学王子，他请黎曼研究实部和虚部在图表绘制中的使用。结果和广义模式最终导致了黎曼Zeta函数，其中所有非平凡零点都在黎曼Zeta函数的实轴上。

实部与虚部图示在某种意义上与收敛模相同。当我们用虚数i（1i）乘以实数时，这类似于90度的角度旋转。通过令s = a + it来找到素数函数的零点，或者黎曼推测所有非平凡零点（t=0的零点不算）都位于s = 1/2 + it处。

计算这些零点实际上非常复杂，因为它们涉及一些复数运算。它通常涉及在复平面上取积分（称为梅林积分），使用黎曼-西格尔公式。这是一个相当复杂的故事，您可以在Odlyzko的页面上找到一些解释（请注意，它涉及FFT算法和许多复杂的数学主题，Odlyzko还拥有关于零点分布的尚未被证明的定理）。

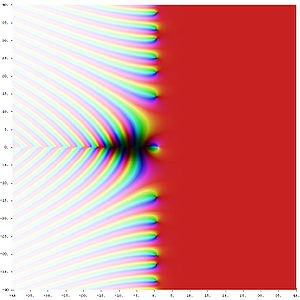
下图显示了黎曼Zeta函数，关键线（实部等于1/2）在此处可见（红色部分从1/2开始）。

还有一个有趣的现象叫做乌拉姆螺旋，以其发明者斯坦尼斯拉夫·乌拉姆（Stanislaw Ulam）的名字命名，他于1963年发现了它。乌拉姆螺旋用于创建素数的简单可视化，揭示了某些二次多项式生成异常多素数的明显趋势。它是在科学会议上展示一篇“冗长乏味的论文”时发现的。它通过将数字写成螺旋状（如下所示）来创建，您可以在维基百科上阅读更多关于它的信息。

该螺旋可以通过球体可视化，球体的大小取决于数字可以被多少个因子整除。下图显示了一个乌拉姆螺旋，该图来自这个网站。

素数被认为是随机的或几乎随机的，这使得很难找到任何模式。如果您看一下埃拉托斯特尼筛法，您已经看到我们可以轻松找到非素数的模式，但素数只能在所有其他模式被排除后才能找到。

自然界中也有一些关于素数随机性的证据。在自然界中，进化特征在于，如果一个物种寻求随机性，您经常会发现素数在起作用。黎曼方程也是如此，您也会得到一个与随机波动一致的误差项。

这个故事还表明，为了找到素数的模式，我们通常将它们视觉化为某种螺旋或圆形的自然数列。几乎所有使用同余模、乌拉姆螺旋和黎曼Zeta函数中黎曼零点的复数进行的计算似乎都与这个事实有关。

阿特金筛法

阿特金筛法（由A.O.L Atkin和Daniel J. Bernstein于2004年创建），这个筛法实际上与埃拉托斯特尼筛法正好相反，它标记非素数而不是素数。有关其推导的详细解释，请参阅创作者的文章这里。该筛法可以分解为以下步骤（来自维基百科）：

所有余数都是模六十余数（将数字除以六十并返回余数）。
所有数字，包括x和y，都是正整数。
翻转筛列表中的一个条目意味着将标记（素数或非素数）更改为相反的标记。
创建一个结果列表，其中包含2、3和5。
创建一个筛列表，其中包含每个正整数的条目；此列表中的所有条目最初应标记为非素数。
对于筛列表中的每个条目号n，其模六十余数为r
如果r是1、13、17、29、37、41、49或53，则翻转每个可能解为4x² + y² = n的条目。
如果r是7、19、31或43，则翻转每个可能解为3x² + y² = n的条目。
如果r是11、23、47或59，则在x > y时，翻转每个可能解为3x² - y² = n的条目。
如果r是其他任何值，则完全忽略。

从筛列表中的最低数字开始。
取筛列表中下一个仍标记为素数的数字。
将该数字包含在结果列表中。
将该数字平方，并将该平方的所有倍数标记为非素数。
重复步骤五到八。
这导致具有奇数个对应方程解的数字被标记为素数，而偶数个解的数字被标记为非素数。

代码基本上是从此处的伪代码转换而来（尽管看到Torleif Berger在这里的C#实现非常有帮助，并且代码几乎完全相同，只是在本篇文章中转换为了VB）。给您一个警告，下面的代码实际上比文章中提供的埃拉托斯特尼筛法算法要慢得多。主要原因是每个二次方程都需要进行复杂的计算和测试。代码仅用于展示其工作原理，如果您确实想实现一个快速的阿特金筛法，您应该使用（或修改）可以在此处下载的C代码。该实现速度更快，因为它使用了程序中预先计算的表。也许有点令人失望，这个算法本质上是一个很好的素数压缩文件。

''' <summary>
''' Returns a list of Primes from 2 to N
''' </summary>
''' <param name="N">Find prime numbers equal or lower than N</param>
''' <returns>List of primes as List(of BigInteger)</returns>
''' <remarks>For large primes you can get out of memory exceptions</remarks>
Private Function SieveOfAtkin(ByVal N As System.Numerics.BigInteger) As List(Of System.Numerics.BigInteger)
    Dim primes As New List(Of System.Numerics.BigInteger)

    Dim isPrime = New Boolean(N) {}
    Dim sqrt As System.Numerics.BigInteger = Math.Sqrt(N)

    For x As System.Numerics.BigInteger = 1 To sqrt
        For y As System.Numerics.BigInteger = 1 To sqrt
            Dim n1 = 4 * x * x + y * y
            If n1 <= N AndAlso (n1 Mod 12 = 1 OrElse n1 Mod 12 = 5) Then
                isPrime(n1) = isPrime(n1) Xor True
            End If

            n1 = 3 * x * x + y * y
            If n1 <= N AndAlso n1 Mod 12 = 7 Then
                isPrime(n1) = isPrime(n1) Xor True
            End If

            n1 = 3 * x * x - y * y
            If x > y AndAlso n1 <= N AndAlso n1 Mod 12 = 11 Then
                isPrime(n1) = isPrime(n1) Xor True
            End If
        Next
    Next

    For n2 As System.Numerics.BigInteger = 5 To sqrt
        If isPrime(n2) Then
            Dim s = n2 * n2
            Dim k As System.Numerics.BigInteger = s
            While k <= N
                isPrime(k) = False
                k += s
            End While
        End If
    Next

    primes.Add(2)
    primes.Add(3)
    For n3 As System.Numerics.BigInteger = 5 To N Step 2
        If isPrime(n3) Then
            primes.Add(n3)
        End If
    Next
    Return primes
End Function

该算法的具体结果如下，我们看到速度有了巨大提升，尤其是在素数变大时。但是，对于一小部分素数，差异并不大：

速度	N/log log N
存储	N^{1/2 + o(1)}

我们现在看到了速度上的提升和存储需求上的巨大差异，尽管它比埃拉托斯特尼筛法要棘手得多。

历史

本文将网络上分散的信息零散地拼凑在一起，如果我忘记包含任何应该包含的参考文献，请接受我最诚挚的歉意。撰写本文的目的是展示用于获取素数的筛法，并为您提供素数的一些性质以及仍未解决的问题的快速概述。

现在您应该拥有一个出色的查找素数工具箱了，您可以直接前往Project Euler网站开始解决问题。您甚至可能开始考虑破解加密的消息，但不应忘记陶哲轩的话，即尚未在数学上证明，如果您能找到一个快速的因数分解公式，您就能破解加密消息。

C#和VB下载中的代码已根据Clifford Nelson发布的替代方案进行了更改。但是我没有更改文章中的代码，因为下载基本上使用了相同的步骤，只是顺序稍有不同。它还大大提高了实现速度，因为它使用了数组而不是列表。

参考文献

我使用的主要来源是一本2001年的书，这本书出版于阿特金筛法发布三年前，因此缺少对近期发现的解释。但是，它仍然包含许多相关材料，并且还描述了素数在现实世界场景中的许多实际应用。

《素数 - 计算视角》，2001年，Richard Cramdall和Carl Pomerance，Springer

《素数音乐》，2004年，Marcus Du Sautoy，Harper Perennial

阿特金筛法的源代码和文章：

其他筛法：

YouTube上David Metzler提供的关于黎曼猜想的精彩视频系列（该系列即使您只懂基础数学也很有用）。

Richard Taylor关于同余模和其他素数方面知识的讲座

素数与方程

Marcus Du Sautoy的视频演示

素数之歌

CodeProject网站上的在线链接：