游戏中的声音 - 墙壁的声学泄漏
4.86/5 (18投票s)
墙壁声学泄漏的数学处理。

引言
这是一篇面向声学专业人士或需要在程序中处理声音的开发者的文章。通过开口处的泄漏是一个非常普遍的问题,尤其是在建筑声学领域,因此在逼真的游戏场景中也同样如此。
值得注意的是,现实世界中关于房间和声源定位的许多信息都直接基于我们的听觉,因为我们常常通过听声音的来源来判断其位置。然而,模拟真实场景是相当复杂的,因为我们利用身体反射来判断声音高度的位置,以及声音从一只耳朵到另一只耳朵的时间差来判断声音的 x-y 位置。对于希望进一步研究的人来说,这种方法在声学中被称为头部相关传递函数 (HRTF)。
因此,这篇文章对于对游戏声学化感兴趣的开发者,或者您想在自己的程序中加入一些声学效果的开发者来说是最有用的。
为了完全理解这篇文章,您需要或应该理解的数学方面包括如何处理
- 具有普通算术运算的复数,以及三角函数
- 涉及积分和微分的基本微积分
- 常微分方程及其解
如果数学内容过于晦涩,我将向您展示一些简单等效的思考问题的方式。您还应该意识到,方程的构建可以使用电阻、电容和电感等效的电路,或者弹簧、粘性阻尼器和质量等效的机械配置。
我用来推导公式的方程比较老式,因为它涉及到贝塞尔函数,该函数是球波方程的通用解之一,因此本文将包含一些在网上文章或博客中不常见的、至少与此问题不直接相关的复杂数学内容。还应该说的是,它也是学习一些基本声学知识的一个很好的起点,因为在许多声学应用场景中,部分内容可以直接迁移。
基本问题定义如下:假设一个来自外部的入射声波(从左向右传播),其入射角基于孔的法线,它穿过孔并从另一侧出来。孔在两侧的直径均为 2a,管子的长度或深度定义为 d。声音的强度降低了多少?

我将通过包含在孔内填充矿棉的效果来扩展原文。这意味着我可以模拟以下情况的影响:
- 一个空的圆形孔
- 在其中一个或两个孔前面放置轻质材料(如管道胶带)
- 在孔内填充矿棉,覆盖整个管道的长度
- 在孔内填充矿棉,并在开口的两侧贴上管道胶带
通过这个程序,您应该能够理解不同配置对最终结果(即内部的声压)的影响。您还应该注意到,在计算中我只计算了法向入射声波,但如果改变入射波的角度 theta,则可以轻松扩展。
背景
在展示方程之前,我将快速给出一些用于构建解决方案的简单类比,或者说您如何思考这个问题。
- 房间或类似的封闭空间可以建模为
电容器或弹簧 - 管道或房间中的泄漏可以建模为
电感器或质量 - 薄管道矩阵可以建模为
电阻器或粘性阻尼器。有关声学概念的进一步研究,您可以参考这篇 文章。
透射波的解实际上是一个滤波器,不同的材料改变一些共振,并在传递函数中添加新的极点或零点。
程序中使用的方法最初来源于边界元法 (BEM) 对波动方程的求解,我将简要解释方程推导的基础。顺便说一句,值得一提的是,声学模拟与可视化问题相对紧密相关,尤其是在高频声学领域。第一个光线追踪计算机程序是由声学家开发的,后来被视觉设计师采用。(您可以在这里 阅读更多关于光线追踪声学开发的编程内容)。
在我描述整个公式之前,先解释一下希腊字母 tau 在这里实际代表的含义。它代表一个常数,将 N/m^2 的压力乘以这个常数,得到墙另一侧的压力,通常表示为 10 *log10 (tau),因为我们非常喜欢在声学中使用对数(痴迷于对数的原因是,我们感知声音响度的感觉与对数函数相关)。完整的通用方程如下所示:

它在大多数情况下都有效,尽管其参数是理想化的,您应该始终记住,如果它在理想化计算中不起作用,那么在现实世界中也不会起作用。
下面对公式中不同元素的简要解释

为了正确理解这里发生的一切,需要对该方程进行一些额外的解释。孔只是一个复杂的滤波器,它会在不同频率下减少或增强输出中的某些效果。通常,当将一个声学方程分解成更小的步骤时,会更容易理解。有几种方法可以做到这一点,但我能想到的最简单的方法是构建一个电路类比

现在我们的方程被分解成简单的步骤,可以单独解释。我们的声源是一个交流电压源,标记为 2Pe,这包括周围介质(即空气)的电阻。
其余部分从左到右依次解释
Zr1,这是开口处的辐射阻抗。这意味着入射波力 F 会通过辐射阻抗的系数转化为运动 u。m1是放置在开口前的潜在物体的质量。这就是管道胶带被模拟的地方。F1是材料m1的弹性,对于管道胶带等薄板材料可以忽略。如果开口未覆盖,m1和F1将不包含在方程中。Z3是从右到左的传播。Z4的两个元素是从一端到另一端的反射波。注意: 只有当管子半径不变且其他一切都对称时,它们的值才相等。m2和F2是可能覆盖出射孔的元素。它们使用与m1和F1类似的方程进行计算。Zr2是出射元件的辐射阻抗,在我们的例子中,它与Zr1相同。
为了检查不同部分,我将首先介绍三种声阻抗
- 比声阻抗。意思是
z = 压力/粒子速度。 - 声阻抗。
Z = 压力 / 体积速度 - 辐射阻抗。
Z<sub>r</sub> = 力 / 粒子速度。
它们在不同的情况下使用,取决于您要解决的方程/问题。然而,在声学中组合方程的一个重要方面是假设粒子速度连续性,这意味着粒子速度不能在一个地方突然改变到另一个地方。在许多需要组合不同类型材料的情况下,理解这一点至关重要。
辐射阻抗
首先定义辐射阻抗:Z = F/u,其中 F 是力,u 是粒子速度,Z 当然是辐射阻抗。通过积分逐步推导这个方程集可能会非常困难,所以我省略了这些步骤,而是引用文章末尾的书籍参考文献。例如,方程的完整推导可以在书《*Fundamentals of Acoustics*》(第 185-186 页)中找到。
![]()
这里,R1 项定义为电阻函数,X1 定义为电抗函数。电阻函数使用贝塞尔方程的解来定义:![]()
X1 项使用斯特鲁维函数计算,如下所示:
![]()
辐射阻抗定义为辐射体对介质施加的力与辐射体速度之比。
''' <summary>
''' Finds the radiation impedance of a circular piston
''' </summary>
''' <param name="radius">The radius of the piston</param>
''' <param name="frequency">The frequency in question</param>
''' <returns>A complex radiation impedance</returns>
''' <remarks></remarks>
Public Function RigidPistonRadiator_
(ByVal radius As Double, ByVal frequency As Double) As Complex
'If the user, for some silly reason puts in 0 or a negative number as the radius
If radius <= 0 Then
Return (New Complex(0, 0))
End If
Dim r1, x1 As Double
'Medium constants
Dim c0 As Double = 340
Dim p0 As Double = 1.21
'Wavenumber
Dim k As Double
k = 2 * System.Math.PI * frequency / c0
'The resistance function
r1 = 1 - (2 * Acoustics.SpecialFunctions.BesselJ_
(2 * k * radius, 1) / (2 * k * radius))
'The reactance function
x1 = 2 * Acoustics.SpecialFunctions.Struve(2 * k * radius, 1) / (2 * k * radius)
'Stor the results from calculation
Dim Result As New Complex(r1, x1)
'Multiply with the caracteristic impedance with area
Result = System.Math.PI * radius ^ 2 * c0 * p0 * Result
Return Result
End Function
质量阻抗
我在建模简单的管道胶带或类似材料的阻尼效应时做了一个简化。为了进行完整的数学处理,您需要包含材料的刚度,但这对于用于本程序的轻质薄材料来说通常是无关紧要的。您实际上可以从这些方程中推导出声学的质量定律。它只是说明,一个被空气包围的薄壁(下式中的 Z<sub>0</sub> 是空气的特性阻抗),在给定频率下的阻尼取决于频率乘以质量(这里我指的是每平方米的总质量)。
![]()
我们继续寻找材料的吸收系数
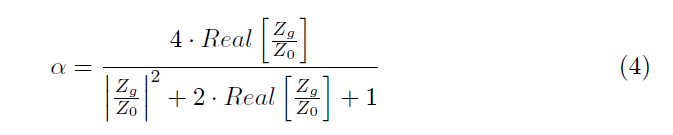
根据我们最初的 Zg 方程,我们的假设中没有内部或任何其他损失,因此它被吸收的唯一方式必须是通过板的另一侧。然后我们写出替换值的解:

还可以计算声音衰减

我们代入空气特性阻抗的值并整理表达式,得到以下方程:
![]()
质量定律在预测普通住宅墙体在低频下的隔声量时经常使用,尽管系数 42.5 会变为 47,因为实际墙体更复杂。它也被认为是低频区域的最大可能衰减水平,此时声音衰减通常由整个墙体的总重量决定。应注意的是,对于简单的均质墙体,它通常相当准确。
通常,它在高频下不适用,因为正常墙体还取决于钉子的共振能力、覆盖板的截止频率以及板之间的距离。声音衰减在高频区域可能远高于质量定律的预测值。
介质中的特性阻抗和传播函数
特性阻抗之所以重要,是因为它可以将粒子速度与压力通过一个常数联系起来,表明其有用性。
![]()
然而,这是非一维波动方程解的一个特例,并不适用于所有情况。它基本上描述了压力波中的电阻乘以粒子速度。
球波的真实解实际上是 Zk = rho C *(jkr/(1+jkr)),只有当 kr >> 1 时,特性阻抗才等于 rho c。
如果假设气流电阻率仅取决于一个常数乘以粒子速度,则可以得到一个一维模型(称为 Rayleigh 模型)来描述介质中的损耗。这是我们拥有的最简单的介质损耗模型,Mechel 在低频区域使用这个简单模型,并在高频区域结合一些经验测量使其拟合。之所以必须使用经验模型,是因为矿物纤维和玻璃纤维材料的复杂配置。这种损耗是介质中正常几何损耗的附加项,但会增加每米的恒定阻尼和相移。本文未包含这方面的详细信息,我将参考这篇 文章。
程序中使用的特殊数学函数
我需要三个特殊函数来使用这个程序,我已将它们放在一个模块中。代码的来源也已提供。它们最初来自 Jack Xu 的著作《*Numerical methods for C#*》(感谢作者允许我发布这部分内容)。但是,Gamma 函数根据提供的参考资料进行了修改,而 Struve 函数是我根据代码注释中提供的维基百科链接实现的。
Namespace Acoustics
Module SpecialFunctions
''' <summary>
''' http://en.wikipedia.org/wiki/Bessel_function#Bessel_functions_of_the_first_kind_:
''' _J.CE.B1
''' </summary>
''' <param name="x">Jv(X) where x is the number and v is the order</param>
''' <param name="v">Bessel function order</param>
''' <returns></returns>
''' <remarks></remarks>
Public Function BesselJ(ByVal x As Double, ByVal v As Double) As Double
Dim sum As Double = 0.0R
Dim term As Double = 0.0R
Dim i As Integer = 0
Do
term = System.Math.Pow(-1, i) * System.Math.Pow(0.5 * x, 2 * i + v) / _
Gamma(i + 1) / Gamma(i + v + 1)
sum += term
i += 1
Loop While System.Math.Abs(term) > 0.000000000001R
Return sum
End Function
''' <summary>
''' http://en.wikipedia.org/wiki/Lanczos_approximation
''' </summary>
''' <param name="x">number x dependent on gamma function</param>
''' <returns>Gamma of the number x</returns>
''' <remarks></remarks>
Public Function Gamma(ByVal x As Double) As Double
Dim g As Integer = 7
Dim p As Double() = {0.99999999999980993, 676.5203681218851, -1259.1392167224028,
771.32342877765313, -176.61502916214059, 12.507343278686905,
-0.13857109526572012, 0.0000099843695780195716, 0.00000015056327351493116}
Dim y As Double
If x < 0.5 Then
Return Math.PI / (Math.Sin(Math.PI * x) * Gamma(1 - x))
End If
x -= 1
y = p(0)
For i As Integer = 1 To g + 1
y += p(i) / (x + i)
Next
Dim z As Double = x + (g + 0.5)
Return System.Math.Sqrt(2 * System.Math.PI) * _
System.Math.Pow(z, x + 0.5) * System.Math.Exp(-z) * y
End Function
''' <summary>
''' http://en.wikipedia.org/wiki/Struve_function#Power_series_expansion
''' </summary>
''' <param name="x">The Hv(x) where x is the number and v is the order</param>
''' <param name="v">Struve function order</param>
''' <returns></returns>
''' <remarks></remarks>
Public Function Struve(ByVal x As Double, ByVal v As Integer) As Double
Dim result, term, sum As Double
'Check if the first term is 0, if so then everything
' would be zero
If (0.5 * x) ^ (v + 1) = 0 Then
Return result
End If
Dim i As Integer = 0
Do
term = ((-1) ^ i) * (0.5 * x) ^ (2 * i)
term = term / (Gamma(i + (3 / 2)) * Gamma(i + v + (3 / 2)))
'Avoid adding NonNumbers as they will cause termination
If Not Double.IsNaN(term) Or Not Double.IsNegativeInfinity(term) Then
sum += term
End If
i += 1
Loop While System.Math.Abs(term) > 0.000000000001R ' i < 100
If Double.IsNegativeInfinity(result * sum) Or Double.IsNaN(result * sum) Then
Return 0
Else
Return result * sum
End If
End Function
End Module
End Namespace
这三个简单的函数在几种不同的声学问题中被频繁使用,并且常常构成许多其他领域数值解的基石。贝塞尔函数确实是波动方程的解,所以这并不奇怪。
Gamma 函数是数学中最通用的函数之一,也是我使用的所有函数的基础,它也可以用于统计学等领域。
历史
这是更新版本,包含了管内多孔材料的阻尼效应,因为我最初只包含了在管道的前面或后面放置轻质覆盖材料的模拟可能性。
您应该知道,该程序本质上非常简单,不包含多孔材料在管内时衰减行为的模拟。结果也归一化到 1 m^2,这意味着它是为了比较不同孔径而创建的。您应该在程序中删除 1/area 项以获得其实际衰减值。
程序可以这样使用:假设墙外有一个噪声源(如道路),在您墙外的每个频率带产生 40 dB(靠近繁忙的交通道路)。这意味着您房间内的噪音将被感知为 40 - 在任何给定频率下的衰减(事情比这更复杂一些,因为它也取决于墙体的衰减以及房间内的混响时间)。
还要感谢 Jack Xu 允许我从他的著作《*Numerical methods for C#*》中包含他的修改后的源代码。
还应指出的是,它通常会低估空孔在高频下的阻尼效应,因为当前的实现没有考虑粘性损耗或其他效应,而这些效应对于空孔可能很重要。对于带板覆盖或矿物纤维,计算结果与预期的阻尼非常吻合。
参考文献
- 《建筑声学》,第一版(2008),Tor Erik Vigran,CRC Press
- 《声学公式》,第二版,F.P. Mechel,Springer
- 《房间声学》,第五版,Heinrich Kuttruff,Spon press
- 《数学函数手册》,Abramowitz and Stegun(1970),Dover
- 《C# 实用数值方法》,Jack Xu,
- 《声学基础》,第四版,Kinsler, Frey, Coppens and Sanders,John Wiley & Sons, Inc.
在线链接
