实现机器学习的分步指南 XI - DBSCAN

Ryukkkk

5.00/5 (2投票s)

2019 年 6 月 18 日

CPOL

4分钟阅读

5927

易于实现的机器学习

引言

基于密度的噪声应用空间聚类 (DBSCAN) 是一种基于密度的聚类算法。与其他聚类算法不同，DBSCAN 将密度可达样本的最大集合视为簇。 KMeans 缺乏对非球形数据进行聚类的能力，而 DBSCAN 可以对任何形状的数据进行聚类。

DBSCAN 模型

预备知识

ε -邻域: 对象 ε 半径范围内的对象。
核心点: 如果一个样本在其 ε-邻域内拥有的点数超过指定数量 (m)，则该样本是一个核心点。
直接密度可达: 如果对象 q 位于对象 p 的 ε-邻域内，并且 p 是一个核心对象，则对象 q 从对象 p 直接密度可达。
密度可达: 如果存在对象链 p1,…,pn，其中 p1=p, pn=q 且对于所有 1 <= i <= n，pi+1 从 pi 直接密度可达，则对象 q 从 p 密度可达（直接密度可达和密度可达的区别在于，直接密度可达时 p 位于 q 的邻域内，而密度可达时 p 不位于 q 的邻域内）。
密度连接: 如果存在一个对象 o，使得 p 和 q 都从 o 密度可达，则对象 p 与对象 q 密度连接。
噪声: 至少不能从一个核心对象密度可达的对象。

让我们举例说明以上术语，如下图所示，其中 m = 4。由于所有红色样本的 ε-邻域内都有超过 m 个样本，因此它们都是核心点和密度可达。 B 和 C 不是核心点。青色圆圈中的样本是直接密度可达。棕色圆圈中的样本是密度连接。 N 无法到达任何其他样本，因此它是一个噪声点。

聚类算法

首先，我们通过计算所有样本 ε-邻域内的样本数来找到所有核心点。剩余的样本暂时标记为噪声点。我们提供几种类型的距离，即

欧几里得距离
$L_{2}(x_{i},x_{j})=\left( \sum_{l=1}^{n}{|x_{i}^{(l)}-x_{j}^{(l)}|^{2}}\right)^\frac{1}{2}$
余弦距离
$\cos\left(x_{i},x_{j}\right)=\frac{x_{i}\cdot x_{j} }{|| x_{i}||\ ||x_{j}||}$
曼哈顿距离
$Mabhatten\left(x_{i},x_{j}\right)=\sum^{n}_{l=1}\left|x_{i}^{(l)}-x_{j}^{(l)}\right|$

    def calculateDistance(self, x1, x2):
        if self.distance_type == "Euclidean":
            d = np.sqrt(np.sum(np.power(x1 - x2, 2), axis=1))
            #d = np.sqrt(np.sum(np.power(x1 - x2, 2)))
        elif self.distance_type == "Cosine":
            d = np.dot(x1, x2)/(np.linalg.norm(x1)*np.linalg.norm(x2))
        elif self.distance_type == "Manhattan":
            d = np.sum(x1 - x2)
        else:
            print("Error Type!")
            sys.exit()
        return d

对于给定的样本，如果该样本与另一个样本之间的距离小于 ε，则它们位于同一个邻域内。

    def getCenters(self, train_data):
        neighbor = {}
        for i in range(len(train_data)):
            distance = self.calculateDistance(train_data[i], train_data)
            index = np.where(distance <= self.eps)[0]
            if len(index) > self.m:
                neighbor[i] = index
        return neighbor

然后，我们随机选择一个未访问的核心点 P 来合并与其密度连接的样本。接下来，我们访问 P 的 ε-邻域内的样本 Q。如果 Q 是一个核心点，则 Q 与 P 属于同一个簇，并在 Q 上执行相同的过程（如深度优先搜索）；否则，访问下一个样本。具体来说，在 P 的 ε-邻域中的搜索过程如下所示

选择核心点 A 并找到其 ε-邻域中的所有样本。 A 的 ε-邻域内的样本属于 A 的簇。然后依次访问 A 的 ε-邻域内的样本。
访问 A 的 ε-邻域内的样本 B。 B 是一个核心样本，访问 B 的 ε-邻域内的样本。
访问 B 的 ε-邻域内的样本 C。 C 属于 A 并且 C 不是一个核心点。访问 B 的 ε-邻域内的其他样本。
访问 B 的 ε-邻域内的另一个样本 D。 D 是一个核心点。访问 D 的 ε-邻域内的样本。
访问样本 E。 E 不是核心点。现在，没有任何点可以密度可达 A。停止对 A 的聚类。

        k = 0
        unvisited = list(range(sample_num))               # samples which are not visited
        while len(centers) > 0:
            visited = []
            visited.extend(unvisited)
            cores = list(centers.keys())
            # choose a random cluster center
            randNum = np.random.randint(0, len(cores))
            core = cores[randNum]
            core_neighbor = []                              # samples in core's neighbor
            core_neighbor.append(core)
            unvisited.remove(core)
            # merege the samples density-connectivity
            while len(core_neighbor) > 0:
                Q = core_neighbor[0]
                del core_neighbor[0]
                if Q in initial_centers.keys():
                    diff = [sample for sample in initial_centers[Q] if sample in unvisited]
                    core_neighbor.extend(diff)
                    unvisited = [sample for sample in unvisited if sample not in diff]
            k += 1
            label[k] = [val for val in visited if val not in unvisited]
            for index in label[k]:
                if index in centers.keys():
                    del centers[index]

参数估计

DBSCAN 算法需要 2 个参数 ε，它指定点彼此之间的距离应该有多近才能被认为是集群的一部分；以及 m，它指定一个点应该有多少个邻居才能包含到集群中。以 wiki 中的一个例子为例，我们计算每个点到其最近邻居的距离，该邻居位于同一分区内，如下所示，我们可以很容易地确定 ε = 22。

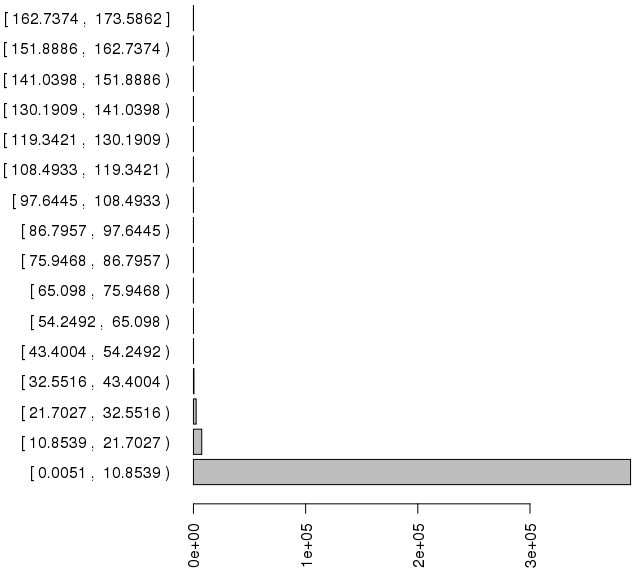
Distribution of distances to the nearest neighbor of each point

对于参数 m，我们计算核心点的 ε 邻域内有多少个样本，如下所示。我们选择 m = 129，因为它是第一个谷底。

Distribution of distances to the number of neighbors

结论与分析

DBSCAN 能够对非球形数据进行聚类，但无法反映高维数据。当密度分布不均匀时，聚类性能不是很好。 KMeans 和 DBSCAN 之间的聚类性能如下所示。很容易发现 DBSCAN 比 KMeans 具有更好的聚类性能。

本文相关的代码和数据集可以在 MachineLearning 中找到。