两条线段交点的魔术公式
5.00/5 (19投票s)
两条线段交点的紧凑且简单的向量公式。

引言
在图形代码领域工作的人员,经常会遇到线段裁剪的问题。这是一个众所周知的问题,已有许多算法被提出。然而,这仍然是一项繁琐的工作,我搜索了一些可行的算法,最终找到了简洁的矢量公式。在本文中,提供了MFC中任意线段裁剪的完整代码示例。
背景
两线段交点的计算基于所谓的向量外积;向量外积有三种完全相同的表示形式

由线段定义的两条直线的交点计算的向量公式

公式 (1) 仅在条件 r1^r0≠0 时有效。同时,很明显在计算机计算中,在使用float和double值时,不可能获得“纯零”。因此,对于编程代码,此条件应表示为

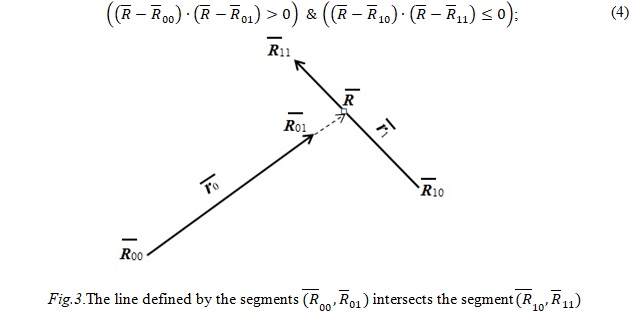
如果条件 (2) 有效,则由线段定义的直线交点R的坐标通过公式 (1) 获得。但尚不清楚线段是否相交。线段的相交性需要通过向量的点积来确定。线段的相交条件如图 2 所示

如果条件 (3) 无效,则线段不相交。尽管如此,向量的点积可能提供有关相关线段相对位置的宝贵信息
另一条线段也同理

以及由线段定义的直线不与线段本身相交的条件

如果条件 (2) 无效,则线段及其定义的直线共线,如果线段不在同一条直线上,则不存在交点。共线向量不在同一条直线上的条件由公式 (7) 中的外积定义,并如图 6 所示

如果条件 (2) 和 (7) 无效,则线段在同一条直线上,可能在某些区域重叠。重叠的条件也可以通过点积来确定,并且区分不同情况是有益的,因为线段可能同向共线(r1∙r0>0)或反向共线(r1∙r0<0),如图 7 和图 8 所示


图 9 提供了共线线段不重叠的条件

以上是一套提供线段相对位置宝贵信息的完整方案。毋庸置疑,这项技术可以应用于任何编程语言。公式 (1) 的主要优点是它可以在图形编程中几乎以本文中的相同形式使用。为了验证上述所有技术,作者在 Visual C++ MFC (Microsoft Foundation Classes) 中开发了一个计算机程序,其中任意线段随机创建、随机旋转和随机移动,并在任意时间进行裁剪,只需按“Enter”键。向量的行为需要根据外积、点积和其他一些特殊例程数学属性来定义。
使用标准的 **MFC App wizard** 创建了演示项目 Segment2D。向量的性能与我在 CodeProject 之前的文章“Weiler-Atherton algorithm in MFC”中的 class Polygon_2D 和 class Vector_2D 相同。线段是随机创建、随机移动和随机旋转的。
在开始构建提供的项目之前,强烈建议您先查看随附的**演示文稿**,以了解预期的输出。
演示说明
该可执行文件Segment2D.exe是使用 **MSVS-2010** 的工具在 **MSVS-2015 pro** 中构建的。因此,Segment2D.exe 即使在 **Windows-XP** 下也有效(与我之前的 CodeProject 文章不同,由于只使用 RAM,因此不需要特殊的 *.dll 文件)。
一些菜单和一些特殊的快捷键已被安排用于演示 **Segment2D 项目**的实现

- 菜单文件->播放 - 播放/停止对象旋转(也按 **Ctrl+P** 键)
- 菜单编辑->重置场景->随机 - 创建具有随机旋转和移动速率的两个任意线段(也按 **空格键**)
- 菜单编辑->重置场景->共线 - 创建具有随机移动速率的两个任意共线线段(也按 **Ctrl+空格键**)
- 菜单编辑->重置场景->重叠 - 创建具有随机移动速率的两个任意在同一直线上的线段(也按 **Alt+空格键**)
- 菜单编辑->开始裁剪 - 停止线段旋转和移动,开始裁剪(也按 **Enter** 键)
- 菜单编辑->下一场景 - 下一场景的性能(如果播放停止;也按 **右箭头**)
- 菜单帮助->帮助 - 显示**帮助对话框**(也按 **F1** 键)
该**帮助对话框**是非模态的,因此您可以直接使用菜单和快捷键命令,或者在**帮助对话框**中按 **OK** 按钮(或双击相应的项)。

构建说明
解决方案配置必须设置为 **Release**,平台设置为 **x86**。
提供的项目是使用 **MSVS-2010** 的工具在 **MSVS-2015 pro** 中开发的。因此,**EXE** 文件即使在 **Windows-XP** 下也有效。如果您不需要在 **Windows-XP** 下运行应用程序,只需将工具更改为 **MSVS-2015** 即可。
默认编码属性为 UNICODE;尽管 MBCS 编码也可用,只需更改属性即可。
即使您是第一次使用 **MSVS**,只需选择菜单 **调试**->**开始执行**(不调试),程序Segment2D.exe应该就会开始构建和运行。
项目源文件和数据存储
Segment2Dproj 路径下的标准源代码是使用标准的 **MFC 应用程序向导**创建的
- Segment2D.cpp - 定义了应用程序的标准类行为
- MainFrm.cpp - 标准
CMainFrame类的实现 - CChildView.cpp - 标准
CWnd类的实现;作者使用标准的 **MFC 应用程序向导**过程创建的消息处理程序 - DlgHelp.cpp - 标准
CDialogEx类的非模态实现;作者使用标准的 **MFC 应用程序向导**过程创建的消息处理程序 - Segment2D.rc 和 resource.h - 作者使用标准的 **资源向导**过程创建的菜单、对话框、快捷键资源
Segment2DProj\GlobUse 路径下的特殊源代码是作者基于标准的**图形**和几何例程过程开发的
- Vector_2D.cpp, Poligon_2D.cpp - 2D 对象处理
代码解释
所有**菜单**和**快捷键**命令均使用标准的 **MFC AppWizard** 技术完成。本文的目的不是解释 Segment2D 演示项目。如有需要,您可以参考我之前的文章“Weiler-Atherton algorithm in MFC”,其中描述了 InitApplication 和 DrawScene Procedure。本文的主要思想是解释**两线段交点“神奇公式”**的用法。
在声明 class Vector_2D 时,向量的主要操作需要预先确定
class Vector_2D : public CObject
{
public:
double x,y;
Vector_2D ( const Vector_2D& v ){ x = v.x; y = v.y;};
Vector_2D(double vx, double vy) { x = vx; y = vy; };
friend Vector_2D operator + ( const Vector_2D&, const Vector_2D& );
friend Vector_2D operator - ( const Vector_2D&, const Vector_2D& );
friend double operator * ( const Vector_2D&, const Vector_2D& );
friend Vector_2D operator * ( double, const Vector_2D& );
friend Vector_2D operator * ( const Vector_2D&, double );
friend Vector_2D operator / ( const Vector_2D&, double );
friend Vector_2D operator / ( const Vector_2D&, const Vector_2D& );
friend Vector_2D operator & ( const Vector_2D& u, const Vector_2D& v )
{ return (u.x + v.x, u.y + v.y);};
friend double operator ^ ( const Vector_2D& u, const Vector_2D& v )
{return (u.x*v.y - u.y*v.x);};
friend double operator | ( const Vector_2D &u, const Vector_2D &v )
{ return (u.x * v.x + u.y * v.y );};
};
inline Vector_2D Normalize ( Vector_2D& v )
{ double vv = !v; return vv > GeomTreshold ? v /vv : Vector_2D(0); };
inline Vector_2D operator + ( const Vector_2D& u, const Vector_2D& v )
{ return Vector_2D( u.x + v.x, u.y + v.y );}
inline Vector_2D operator - ( const Vector_2D& u, const Vector_2D& v )
{ return Vector_2D( u.x - v.x, u.y - v.y );}
inline double operator * ( const Vector_2D& u, const Vector_2D& v )
{ return u.x * v.x + u.y * v.y;}
inline Vector_2D operator * ( const Vector_2D& u, double f )
{ return Vector_2D( u.x * f, u.y * f);}
inline Vector_2D operator * ( double f, const Vector_2D& u )
{return Vector_2D( f * u.x , f * u.y );}
inline Vector_2D operator / ( const Vector_2D& u, double f )
{ return Vector_2D( u.x / f, u.y / f );}
inline Vector_2D& Vector_2D::operator += ( const Vector_2D& v )
{ x += v.x; y += v.y; return * this;}
inline Vector_2D& Vector_2D::operator -= ( const Vector_2D& v )
{ x -= v.x; y -= v.y; return * this;}
inline Vector_2D& Vector_2D::operator *= ( double v ){ x *= v; y *= v; return * this;}
inline Vector_2D& Vector_2D::operator *= ( const Vector_2D& v )
{ x *= v.x; y *= v.y; return * this;}
inline Vector_2D& Vector_2D::operator /= ( double v ){ x /= v; y /= v; return * this;}
两条直线(由线段定义)的交点是计算在同一条直线上的
Vector_2D R = (r0 * (R11^R10) - r1 *(R01^R00)) / (r1^r0);
一旦由接收到的线段确定了两条直线的交点,就可以很容易地估计该点是否属于线段,方法是使用本文背景部分规定的点积计算。
由以下函数计算的共线线段的重叠条件
BOOL isOverlapping(Vector_2D R00, Vector_2D R01, Vector_2D R10,
Vector_2D R11, Vector_2D * Q0, Vector_2D * Q1)
{
Vector_2D r0 = R01 - R00;
Vector_2D r1 = R11 - R10;
if (fabs(r1^r0 / (!r1 * !r0)) > GeomTreshold)
return FALSE;
if (fabs((R10 - R00) ^ r0 / (!(R10 - R00) * !r0)) > GeomTreshold)
return FALSE;
if(r0*r1 >0) //if segments in same direction
if ((R00 - R10)* (R00 - R11) <= 0) //if R00 is inside the segment(R10, R11)
{
*Q0 = R00;
if ((R01 - R10)* (R01 - R11) <= 0) //if R01 is inside the segment(R10, R11)
*Q1 = R01;
else
*Q1 = R11;
}
else
if ((R10 - R00)* (R10 - R01) < 0) //if R10 is inside the segment(R00, R01)
{
*Q0 = R10;
if ((R01 - R10)* (R01 - R11) <= 0) //if R01 is inside the segment(R10, R11)
*Q1 = R01;
else
*Q1 = R11;
}
else;
else //if segments in contrary direction
if ((R00 - R10)* (R00 - R11) <= 0) //if R00 is inside the segment(R10, R11)
{
*Q0 = R00;
if ((R01 - R10)* (R01 - R11) <= 0) //if R01 is inside the segment(R10, R11)
*Q1 = R01;
else
*Q1 = R10;
}
else
if ((R11 - R00)* (R11 - R01) < 0) //if R11 is inside the segment(R00, R01)
{
*Q0 = R11;
if ((R01 - R10)* (R01 - R11) <= 0) //if R01 is inside the segment(R10, R11)
*Q1 = R01;
else
*Q1 = R10;
}
else
return FALSE;
return TRUE;
}
}
使用提供的项目开发您自己的应用程序
我希望本文背景部分的解释非常清楚,以便每个人都可以在任何编程语言中使用这项技术。
您可以直接使用整个项目,并将其重命名为我在 CodeProject 之前的文章“MFC Project from Existing Code in One Click”中的项目,然后根据需要合并和改进代码。
或者,您可以从本项目中选取 GlobUse **目录,并通过菜单**项目->现有项**将其包含到**任何您自己的图形项目中**,其中包含特殊过程。
如果您引用我的代码,将不胜感激。
关注点
最有趣的一点是,为什么我在任何权威来源都没有找到这个“神奇公式”。它很容易使用,即使是学校级别的几何知识。当然,如果我们展开这个公式,使用标准的坐标表示,最终应该会得到一个巨大的算法,就像网上提供的许多算法一样。但我敢肯定,在使用了这个公式之后,很少有人会回到那些枯燥的程序。
我相信这个演示和代码对于软件人员进行线段裁剪应该会有所帮助。
该项目是在 **MFC 平台**上开发的。然而,在 **MFC** 中开发的所有内容都可以转换为 **Win32**,反之亦然。
本文标题中的 gif 是由我在 CodeProject 之前的文章“Your Own Avishop”中的程序创建的。
历史
- 2019年12月5日:初版
