Simulink Matlab 中的数据驱动模型预测控制器 (MPC)

引言

本文在 Simulink Matlab 中实现了一个数据驱动模型预测控制器（MPC）。该控制器利用了原始系统提供的在线数据和期望信号。实际上，控制器通过评估控制输入来尝试使系统的输出达到期望信号。控制输入是控制器的输出，应用于原始系统。因此，控制器具有两个输入和一个输出端口，分别为系统输出、期望参考信号和控制输入。该控制器实现为一个 Simulink 子系统，可以通过双击该子系统并插入随后的控制器参数来轻松修改其参数。

开发的子系统对真实系统的输出和输入拟合了一个 ARIMA 模型。然后，将 MPC 应用于在线估计的 ARIMA 模型以实现控制目标。主要的控制目标是将系统输出达到期望的参考信号。随后，将开发的子系统显示出来。

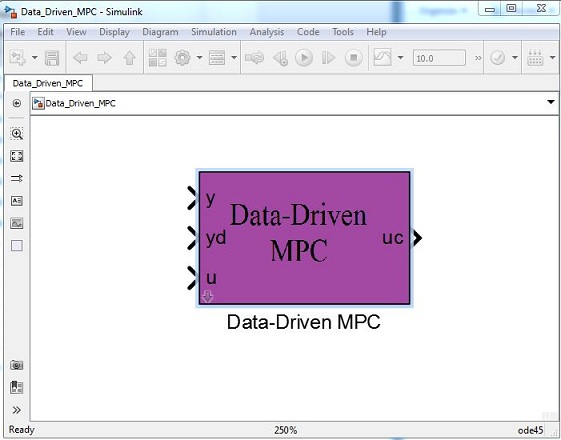
如上图所示，开发的子系统可以通过将其端口连接到希望控制的原始系统来直接使用。

背景

如前所述，开发的 Simulink 子系统同时实现了在线模型拟合和模型预测控制器（MPC）。第一步，考虑一个 ARIMA 模型，如下所示：

y(t)=A1*y(t-1)+A2*y(t-2)+...+Ap*y(t-p)+B1*u(t-1)+B2*u(t-2)+...+Bq*u(t-q)

其中 y(t) 和 u(t) 是原始系统的输出和输入。参数 mu 和 my 分别代表原始系统的输出和输入数量。此外，参数 p 和 q 是上述方程中使用的 ARIMA 模型的阶数。可以通过更改子系统参数中的这些参数来手动修改它们。开发的子系统将一个类似上述模型的模型拟合到原始系统的输入和输出上，而原始系统的内部属性被假定为完全未知。

第二步，将一个合适的 MPC 应用于获得的 ARIMA 模型。控制器尝试通过基于 MPC 的思想来设计控制序列，使系统输出 y(t) 达到期望的参考信号 yd(t)。控制器参数，包括预测和控制时域，在开发的子系统中由 Ny 和 Nu 表示。事实上，控制器按如下方式预测未来步长的系统输出 y(t)：

y(t+1)=A1*y(t)+A2*y(t-1)+...+Ap*y(t-p+1)+B1*U(t)+B2*u(t-1)+...+Bq*u(t-q+1)

y(t+2)=A1*y(t+1)+A2*y(t)+...+Ap*y(t-p+2)+B1*U(t+1)+B2*U(t)+B3*u(t-1)...+Bq*u(t-q+2)

...

y(t+Ny)=A1*y(t+Ny-1)+A2*y(t+Ny-2)+...+Ap*y(t+Ny-p)+B1*U(t+Ny-1)+B2*U(Ny-2)+...

然后，控制器精确地确定控制序列 U=[U(t) U(t+1) ... U(t+Nu-1)]，使得预测输出 Y=[y(t+1) y(t+2) ... y(t+Ny)] 接近参考信号 yd(t)。为此，定义并求解一个优化问题，以最优地确定控制序列 U。在每一步 t 获得最优控制序列，并将其第一个条目作为控制输入应用于原始系统。

需要注意的是，开发的子系统可用于 SISO 和 MIMO 系统。这意味着系统可以有多个输出和输入端口。

Using the Code

在本小节中，将通过一些示例提供有关开发子系统使用的说明性注释。

在第一个示例中，假设希望控制 LTI 系统 1/(s+1) 以跟随正弦波参考信号，如下所示：

上图简单描述了如何在 Simulink 中使用开发的控制器。为此，实现了原始系统（即 1/(s+1)），并将其输出连接到数据驱动 MPC 的“y”端口，同时将数据驱动 MPC 的“uc”端口连接到其输入。期望的参考信号被视为一个正弦波，其参数可以修改。然后，控制器尝试将原始系统的输出信号闭合成期望的信号。

通过单击数据驱动 MPC，将显示以下属性：

上述参数中的一些是预先定义的，而另一些则在此处定义。参数“T”代表时间步长。参数“umin”、“umax”和“udmax”分别代表控制输入信号的最小值、最大值和时间导数最大值。所有这些参数都可以根据原始系统的限制进行更改。接下来，将显示系统输出及其期望信号，以评估控制器的性能。

可以看出，控制器正确地控制了系统。

在第二个示例中，将数据驱动 MPC 应用于水箱系统以控制其水位。此示例的详细信息在附件文件中的 Example2.slx 中给出，此处显示：

期望的水位设置为 2，并利用数据驱动 MPC 实现此控制目标。即使对原始系统（本例中为水箱系统）的内部信息一无所知，也可以轻松使用该控制器。控制器的参数可以根据操作员的限制和命令进行调整。下图显示了系统输出信号的适当跟踪。

上图揭示了所实现控制器在本例中控制水位的能力。

开发的子系统使用了一个名为 myfun 的脚本，该脚本模拟了在线估计和 MPC 设计。代码如下：

//
function Z=myfun(y,yref,u,t,umin,umax,udmax,p,q,my,mu,Ny,Nu,T,th0,P0)
global U Y P th Uo yh;
U=[U(2:end,:);u'];
if t==0      
    P=P0;th=th0;
    U=zeros(q,mu);Y=zeros(p,my);
    Uo=zeros(Nu,mu);    
end
H=zeros(my,my^2*p+my*mu*q);
ind=1;
for i=1:p
    H(:,ind:ind+my^2-1)=kron(Y(p-i+1,:),eye(my));ind=ind+my^2;
end
for i=1:q
    H(:,ind:ind+my*mu-1)=kron(U(q-i+1,:),eye(my));ind=ind+my*mu;
end
H=H';
m=size(H,2);
L=(P*H)/(eye(m)+H'*P*H);
P=P-L*H'*P;
th=th+L*(y'-H'*th);
yh=zeros(my,1);
for i=1:p
    ind=1+(i-1)*my^2;
    Ai=reshape(th(ind:ind+my*my-1),my,my);
    yh=yh+Ai*Y(p-i+1,:)';
end
for i=1:q
    ind=1+p*my^2+(i-1)*my*mu;
    Bi=reshape(th(ind:ind+my*mu-1),my,mu);
    yh=yh+Bi*U(q-i+1,:)';
end
Y=[Y(2:end,:);y'];
umin=reshape(umin,length(umin),1);
umax=reshape(umax,length(umax),1);
udmax=reshape(udmax,length(udmax),1);
G=zeros(Ny*my,Nu*mu);g=zeros(Ny*my,1);
for i=1:Ny
    Ge=zeros(my,size(G,2));ge=zeros(my,1);
    for j=1:p
        ind=1+(j-1)*my^2;
        Aj=reshape(th(ind:ind+my*my-1),my,my);
        if j>=i
            ge=ge+Aj*Y(end-j+i,:)';
        else
            Gw=G((i-j-1)*my+1:(i-j)*my,:);
            gw=g((i-j-1)*my+1:(i-j)*my,:);
            Ge=Ge+Aj*Gw;
            ge=ge+Aj*gw;
        end
    end
    for j=1:q
        ind=1+p*my^2+(j-1)*my*mu;
        Bj=reshape(th(ind:ind+my*mu-1),my,mu);
        if j>i
            ge=ge+Bj*U(end-j+i+1,:)';
        elseif i-j+1<=Nu
            Ge(:,(i-j)*mu+1:(i-j+1)*mu)=Ge(:,(i-j)*mu+1:(i-j+1)*mu)+Bj;
        end
    end
    G((i-1)*my+1:i*my,:)=Ge;
    g((i-1)*my+1:i*my,:)=ge;
end
z1=ones(Nu,1);
if ~isempty(udmax)
    A1=eye(Nu*mu);b1=Uo+T*kron(z1,udmax);
    A2=-eye(Nu*mu);b2=-Uo+T*kron(z1,udmax);
    A=[A1;A2];b=[b1;b2];
else
    A=[];b=[];
end
if ~isempty(umin)
    Umin=kron(z1,umin);
else
    Umin=[];
end
if ~isempty(umax)
    Umax=kron(z1,umax);
else
    Umax=[];
end
Yref=kron(ones(Ny,1),yref);
gb=g-Yref;
opt=optimset('disp','none');
Uo=quadprog(2*(G'*G),2*G'*gb,A,b,[],[],Umin,Umax,Uo,opt);
uc=Uo(1:mu);
Z=[uc;yh];
end
//

上述代码在开发的子系统内部使用，解释了数据驱动 MPC 的实现方式。

关注点

通过将其插入任何控制回路，可以轻松使用此 Simulink 子系统。该子系统可在科学论文中用作对比控制器，以评估您开发的控制器的性能。

历史

• 2020年10月18日：初始版本