有趣的有限状态机:使用破解的正则表达式逐步解析数字。
4.16/5 (9投票s)
利用正则表达式让你的电脑为你工作。
引言
现在来点完全不一样的东西。这篇文章的灵感来自于我最近的一次编码冒险,在那里我开始着手解决一个问题。我如何解析一个长度不确定的数字,这个数字可能大到无法一次性加载到内存中?atoi()和strtod()在这里会失效。你可能怀疑我正在编写一个任意精度库。我没有,但它可以适应一个库,因为其中的原理在解析方面是相似的。我的目标是以值空间中的JSON数字的最佳近似值来呈现,同时也在词法空间中保留它,以便进行往返。例如,如果你有百万位数的pi,至少用标准的浮点数来说,你是不可能将它保存在值空间中的。充其量,你只能近似它。然而,没有什么理由你不应该能够将整个数字保留为一串字符,特别是如果你可以分块流式传输它。但是如何同时做到这两点呢?我需要解决这个问题,现在我将向你展示我是如何做到的。
必备组件
- 你需要一台目前没有着火的电脑。
- 希望它上面有一个C++编译器。
- 它上面也应该有.NET。我在Linux上使用MonoDevelop,但相关的代码——或者我应该说可疑的代码——将在Windows上运行,并且可以从Visual Studio中运行。
- 说到代码,你需要从这篇文章中获取代码,因为我们正是用它来生成我们要移植的C#状态机。代码有些过时,但非常适合这个目的。我在上面也提供了链接。
- 你可能需要安装Graphviz,至少如果你想要一个漂亮的流程图来配合状态机的话。这比盯着一堆
if语句包围的switch要好。
概念化这个混乱的局面
我喜欢状态机。如果我能用一个状态机解决问题,我就会兴奋不已。它们的问题在于维护起来非常困难,所以我宁愿让电脑尽可能地处理这个问题,尽管并非总是可能。即使那样,我仍然可以使用电脑来帮助我编写代码,然后我可以修改它。生成的代码很丑陋,但至少在我触碰它之前是没有bug的。
在这种情况下,我们将使用状态机来制作一种协程——一种可重启动的方法。C++20中有这些,但剧透一下,编译器会在你的代码中构建状态机来让它们工作。由于我出于某些原因针对C++11,我没有那些。C++20相对较新,你可能也没有。如果你有,哇,你真时髦!你可以跳过这个混乱,除非你感兴趣,但有了你闪亮的新编译器,你就有更少 hacky 的选择了。
协程基本上是一种被迭代分解的方法。它每次被调用时执行其总功能的一部分。传统的函数只被调用一次,执行一个完整的工作单元然后返回。协程被调用多次,每次执行一小部分工作然后将控制权返回给调用者。协程对于协作多线程很有用,因为它们通常不会阻塞很长时间。它们对于非常相似的东西也很有用——迭代解析,而这正是我们要做的。它们在某种程度上是“异步的”,因为它们实际上是非阻塞的,但对我们来说更重要的是,它们可以一次处理一小部分数据,这意味着我们可以,例如,从磁盘读取一个字符,解析它,然后移动到下一个值,然后重复。
正如我所说,我宁愿尽可能地让我的电脑为我做工作,因为它比我更擅长编程,就避免的bug数量而言。而且我懒。
我并不介意威胁我的电脑,但我发现通过诡计让它做我想要的事情更有效。在这种情况下,我将愚弄它,让它以为它正在生成漂亮的图形和C#代码来匹配正则表达式。它实际上是在为我提供一个我不想从头开始编写的状态机的蓝图,并且还给我一个流程图来跟踪它。
在我意识到状态机*和正则表达式在数学上几乎是可互换的、可以相互转换的时候,我就决定我真的很喜欢正则表达式。它们基本上是一种非常简洁的函数式编程语言,只有几个基本运算符:()|?*,其余的都是语法糖或回溯,那是另一回事。我之前链接的文章介绍了运算符,但我在这里的文章末尾也介绍了它们。这种表达式的输出是一个状态机。我们将利用这一点。
*我偷懒了。具体来说,这适用于两类有限状态机——DFA和NFA,而不是所有状态机。我声称有文学创作许可。
如果你错过了,我们将使用正则表达式来创建协程的基础。
如果这个马戏团里还没有够多的丑角,我们将用C#创建那个协程,然后让电脑用更多的正则表达式把它移植到C。到处都是正则表达式。
最后,我们将用逻辑来增强它,以累积解析的字符到一个数字。
一切都始于正则表达式:(\-?)(0|[1-9][0-9]*)((\.[0-9]+)?([Ee][\+\-]?[0-9]+)?)
这代表一个有效的JSON数字。它不能有多余的前导零。它不能以.开头。它可能有一个小数部分和一个指数部分。指数部分可以表示为E10、E+10或e-10。
如果你看一下正则表达式,如果你眯着眼睛看,你可以在里面看到其中一些规则。我对此很擅长,因为我有一些奇怪的爱好。
总之,用一个漂亮的小图可能会更容易
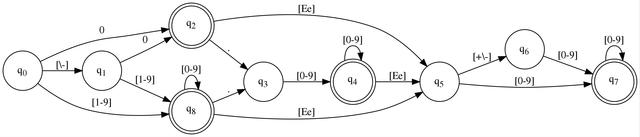
这是“蛇梯棋”®!当看到它上面的字符时,沿着黑线走,其中\只是一个转义符,[0-9]表示数字范围。每次你进入一个新气泡,你就前进一个输入字符,所以例如,你只会调用fgetc()一次来获取下一个字符。你一直走,直到没有更多的移动。如果你完成后,停在一个双圆圈上,你就赢了。否则,你就输了。我在开玩笑。双圆圈意味着我们刚刚读取的值是有效的。如果我们必须停止,并且我们不在双圆圈上,这意味着它是无效的。
现在,我要告诉你这个图是从那个正则表达式生成的。问题是,你是不是那种会随便相信陌生人的人?如果你不相信我——也许你不应该,因为我以夸大其词而闻名——那么请阅读我在前提条件部分发布的文章,它对这个过程进行了相当详尽的处理。
冥想一下这张图。那里有代码,如果你眯着眼睛看。把它想象成一个goto表。每个气泡代表一个你可以goto的标签,每条线代表一个你可以前进的条件。隐含的部分是条件的比较对象,它是你正在读取的输入源的当前字符。每次你沿着一条线(goto)走,你就前进一个输入。
记住这一点,这样我接下来要展示的就不会被当作巫术。我之前被指责过,而且总是非常尴尬。
使用这个烂摊子
让我们从解压那个旧代码库开始。转到RegexDemo项目,毫不留情地快速、有 conviction 地清除Project.cs的Main()函数中的代码——在它有机会存活之前。
var fa = RegexExpression.Parse(@"(\-?)(0|([1-9][0-9]*))
((\.[0-9]+)?([Ee][\+\-]?[0-9]+)?)").ToFA<string>();
fa.RenderToFile(string.Join(Path.DirectorySeparatorChar.ToString(),
new string[] { "..", "..", "flt_nfa.jpg" }));
fa = fa.Reduce();
fa = fa.ToDfa();
fa.TrimDuplicates();
// HACK: Apparently there's an old bug in my DFA table creation.
// It doesn't matter because I have a new algo anyway but this code
// is ancient. We just correct the output here:
// remove all transitions from q2 to q4
var cl = fa.FillClosure();
var q2 = cl[2];
var q4 = cl[4];
var l = q2.FillClosure();
var r = new List<char>();
foreach(var f in l)
{
// get our transitions dictionary backward
var d = (IDictionary<CharFA<string>, ICollection<char>>)f.InputTransitions;
ICollection<char> c;
if (d.TryGetValue(q4, out c))
{
foreach (var ch in c)
{
r.Add(ch);
}
}
}
foreach(var ch in r)
{
q2.InputTransitions.Remove(ch);
}
fa.RenderToFile(string.Join(Path.DirectorySeparatorChar.ToString(),
new string[] { "..", "..", "flt_dfa.jpg" }));
var dfaTable = fa.ToDfaStateTable();
var method = CharFA<string>.GenerateLexMethod(dfaTable, -1);
var cd = CodeDomProvider.CreateProvider("c#");
var w = new StringWriter();
cd.GenerateCodeFromMember(method, w, new CodeGeneratorOptions());
var s = w.ToString().Replace("context.CaptureCurrent();" + Environment.NewLine, "");
s = s.Replace(" context.Advance()", "*pch = fgetc(pfile)");
s = s.Replace("context.Current", "*pch");
s=Regex.Replace(s, "goto q([0-9]+);",
"*pstate = $1;" + Environment.NewLine + " return 1;");
s = s.Replace("goto q", "*pstate = ");
s = s.Replace("return 0;", "*paccept = 1;\r\n return -1 != *pch;");
s = s.Replace("error:" + Environment.NewLine, "}"+Environment.NewLine+"error:" +
Environment.NewLine + " ");
s = s.Replace("context.EnsureStarted();", "switch(*pstate) {");
s = s.Replace(" // q0", "case 0:");
s = Regex.Replace(s,"q([0-9]+):", "case $1:");
s = s.Replace("return -1;", "return 0;");
s = s.Replace("internal static int Lex(RE.ParseContext context)",
"#include <stdio.h>\r\n#define LEXNUM1\r\nint lexnum
(FILE* pfile,int* pstate,int* pch,int* paccept)");
s = Regex.Replace(s,@"if \(\(\*pch == '([0-9]|\.|\-|E|e|\+)'\)\)", @"if (*pch == '$1')");
Console.WriteLine(s);
用这个替换它。在文件顶部添加它会报错的using语句,比如System.Text.RegularExpressions。RenderToFile()中的奇怪数组是为了构建Windows用户的路径,因为他们……不一样。它会将flt_nfa.jpg和flt_dfa.jpg转储到你的RegexDemo项目目录,但前提是你安装了GraphViz。否则,如果你不注释掉RenderToFile()行,它会抱怨,你就得忍受没有图片的痛苦。两者中,后者直接更有用,但也同样更令人困惑。它是由前者生成的,表示相同的流程,但更容易理解。灰色虚线表示在没有输入时进行移动。再次,请参阅我链接的文章以了解如何阅读NFA图。或者不看。随你便,让我伤心吧。
这些替换用于将C#代码转换为C。我们在这里只需要几个正则表达式,但我挑战任何说它们不极其有用的人动手。这才是这一切的意义所在。我们刚刚用它们来教电脑C,而它甚至不那么聪明。
注意:敏锐的读者,我指的是那些目前没有严重头部受伤的人,可能已经注意到了上面代码中一个相当糟糕的hack。“HACK:”是我们微妙的提示。ToDfa()例程显然有问题,会生成不正确的DFA……有时。否则,我早就应该在这篇文章之前就发现了……也许吧。总之,在这种情况下,它会从q2创建错误的过渡到q4,而这些过渡本不应该存在。我在代码中移除了它们。你们可以开始公开羞辱我了,因为我罪有应得。我早就转向了一个新的算法,它更快,更重要的是,是正确的——因为我没有想出它。另外,它支持Unicode,我们这里不需要,但它生成的是表,而不是代码,这对我们这种情况来说用处不大。我最终会生成一个C和C++的代码生成器,以从一开始就避免所有这些问题。
总之,它将一些难看的代码转储到控制台。你需要将它粘贴到你最喜欢的——或者说你拥有的最不糟糕的C++编辑器中,因为我们要对它进行修改。
#include <stdio.h>
#define LEXNUM1
int lexnum(FILE* pfile,int* pstate,int* pch,int* paccept) {
switch(*pstate) {
case 0:
if (*pch == '-') {
*pch = fgetc(pfile);
*pstate = 1;
return 1;
}
if (*pch == '0') {
*pch = fgetc(pfile);
*pstate = 2;
return 1;
}
if (((*pch >= '1')
&& (*pch <= '9'))) {
*pch = fgetc(pfile);
*pstate = 8;
return 1;
}
goto error;
case 1:
if (*pch == '0') {
*pch = fgetc(pfile);
*pstate = 2;
return 1;
}
if (((*pch >= '1')
&& (*pch <= '9'))) {
*pch = fgetc(pfile);
*pstate = 8;
return 1;
}
goto error;
case 2:
if (*pch == '.') {
*pch = fgetc(pfile);
*pstate = 3;
return 1;
}
if (((*pch == 'E')
|| (*pch == 'e'))) {
*pch = fgetc(pfile);
*pstate = 5;
return 1;
}
*paccept = 1;
return -1 != *pch;
case 3:
if (((*pch >= '0')
&& (*pch <= '9'))) {
*pch = fgetc(pfile);
*pstate = 4;
return 1;
}
goto error;
case 4:
if (((*pch == 'E')
|| (*pch == 'e'))) {
*pch = fgetc(pfile);
*pstate = 5;
return 1;
}
if (((*pch >= '0')
&& (*pch <= '9'))) {
*pch = fgetc(pfile);
*pstate = 4;
return 1;
}
*paccept = 1;
return -1 != *pch;
case 5:
if (((*pch == '+')
|| (*pch == '-'))) {
*pch = fgetc(pfile);
*pstate = 6;
return 1;
}
if (((*pch >= '0')
&& (*pch <= '9'))) {
*pch = fgetc(pfile);
*pstate = 7;
return 1;
}
goto error;
case 6:
if (((*pch >= '0')
&& (*pch <= '9'))) {
*pch = fgetc(pfile);
*pstate = 7;
return 1;
}
goto error;
case 7:
if (((*pch >= '0')
&& (*pch <= '9'))) {
*pch = fgetc(pfile);
*pstate = 7;
return 1;
}
*paccept = 1;
return -1 != *pch;
case 8:
if (*pch == '.') {
*pch = fgetc(pfile);
*pstate = 3;
return 1;
}
if (((*pch == 'E')
|| (*pch == 'e'))) {
*pch = fgetc(pfile);
*pstate = 5;
return 1;
}
if (((*pch >= '0')
&& (*pch <= '9'))) {
*pch = fgetc(pfile);
*pstate = 8;
return 1;
}
*paccept = 1;
return -1 != *pch;
}
error:
*pch = fgetc(pfile);
return 0;
}
格式有点糟糕,但你可以通过在编辑器中对switch主体进行制表来修复它,或者如果你有的话,使用它的高级自动格式化功能。将其保存为项目中的lexnum1.h。
还记得我说每个气泡都用一个标签来表示吗?别担心,我不会骗你(除非有足够的诱因)。它们现在已经被case x取代了,其中x是状态的id,所以q0是case 0。我们的范围表达式[...]已被替换为if测试中的>=和<=比较。否则,单个字符比较使用==,两者结合起来就代表了图中的线条。我们使用fgetc()从输入中获取字符来进行演示。显然,使用fgetc()是相当有限的,但选择它的原因在于它很容易被替换成其他东西。它的返回值和整体用法再简单不过了,而且容易模拟。我在这里尽力为你提供方便。当我们到达一个双圆圈状态时,我们将*paccept设置为一个非零值,并且只有在我们没有从fgetc()收到EOF信号时才建议读取更多字符。这段代码有点令人困惑,所以稍后我们将使用电脑生成的jpg来帮助我们理解它。
一个细微之处是,fgetc()会前进并返回下一个字符,而C#代码调用Advance(),它将下一个字符读取到Current中。这意味着我们必须先调用一次fgetc()来“预热”机器并提供一个起始字符(这正是EnsureStarted()在C#代码中隐含的功能),并且我们还必须将我们读取的最后一个字符作为机器状态的一部分保留下来,以替换曾经的Current。
另外,原始的C#代码不是协程——在实际的协程中,我们不需要goto,而是需要return,并在下次被调用时接续之前的地方。这可以通过保留一个pstate参数来实现,并将标签替换为switch(pstate),以及每个标签的case。这是一个直接的翻译,因为这已经是一个状态机了,它只是被构建成完全在一个例程调用中执行,我们使用了简单的字符串匹配来改变上面的内容。这说明了翻译的直接程度。
然而,我们需要添加实际的解析代码来使其更有价值。我的意思是,我们需要有代码将来自fgetc()的字符流转换为数字,因为谁不喜欢数字呢?状态机相关的jpg图实际上使这变得容易。我们可以识别图中的线条,在这些线条上我们需要做一些事情,比如乘以10然后加上下一个数字,这告诉我们必须在那些糟糕的代码中放置我们的计算。
辛勤工作。我知道,但想象一下你亲手写了那些胡言乱语。你不仅要面对一次极其残酷且可能带有暴力的代码审查,而且解析数字看起来很简单,直到你真的去做。有很多角落情况需要考虑。如果你不让电脑生成代码,那就意味着你必须自己做,谁需要那种虐待?幸运的是,我们的电脑很迟钝,但也很积极,你可以说服它们为我们做大部分工作。
首先,为了节省你实际跟随并下载与文章配套的代码的麻烦,我将把驱动代码放在main.cpp中,因为编程的本质就是复制粘贴,至少我从问答部分学到了这一点。
#include <stdio.h>
#include "lexnum1.h"
#ifdef LEXNUM1
int main(int argc,char** argv) {
// create one char strings:
char sz[2];
sz[1]=0;
int state = 0;
int accept = 0;
FILE* pfile = fopen("pi.txt","r");
if(!pfile) {
printf("Could not open pi.txt\r\n");
return -1;
}
int ch = fgetc(pfile);
if(0>ch) {
printf("pi.txt was empty\r\n");
fclose(pfile);
return -1;
}
sz[0]=ch;
printf("%s",sz);
// lexnum is a coroutine. we call it repeatedly
// and each time it performs just on character
// of the parse. It's done when it returns 0
while(lexnum(pfile,&state,&ch,&accept)) {
if(-1<ch) {
sz[0]=ch;
printf("%s",sz);
}
}
printf("\r\n");
if(0!=accept) {
printf("Accepted number\r\n");
} else {
printf("Rejected number\r\n");
}
fclose(pfile);
}
#endif
这就是我们要实现的神奇之处。现在我们可以以流式、逐字符的方式验证数字了。
我们需要创建pi.txt文件,并在其中放入3.141592653589793238462643,尽管任何记住这么多pi的人可能都有社交障碍,这就是为什么我十几岁时会开始研究它。
现在运行它,我们得到
Accepted number
如果我们弄乱了pi.txt中的数字,我们得到
Rejected number
太棒了,有进展了!
当然,验证并不是真正的最终目标。我们想把这个东西解析到值空间——一个数字表示。为了做到这一点,我们需要一个累加器和一些额外的状态。与其给lexnum()函数添加更多参数,不如把它改成接受一个struct。同时,我们将添加那些额外的信息,然后我将在事后解释,因为我就是这么难缠。
struct lex_info {
FILE *pfile;
int state;
int ch;
int accept;
int neg;
int overflow;
double value;
int frac_count;
int e_neg;
int e_count;
};
这就是我们现在传递给lexnum2.h中的lexnum()的。你会找到相应的pfile、state、ch和accept,但我们有几个新的数据项。我通过搜索和替换的魔法创建了lexnum2.h,这是现代的奇迹。如果一开始就用C#代码来做会更容易,但我将其分解为单独的步骤来演示。这就是我将要介绍的关于lexnum()的这一迭代的所有内容。你会在项目中找到新的驱动代码在main.cpp中,以及相应的头文件。
这些包含了足够的信息来跟踪我们在解析中的位置,以及我们迄今为止累积的value,以便做到这一点。老实说,使用int对所有东西来说都有些过度——例如,我们可以用一个6位的frac_count,然后用1位表示neg,用1位表示overflow,但我不想使演示变得复杂。neg告诉我们数字是否为负,frac_count告诉我们已经解析了多少个小数位数,overflow告诉我们它是否太大而无法在值空间中准确表示,e_neg告诉我们e_count是否为负,而e_count则保存e后面的数字(如果有)。
现在我们要修改状态机,因为谁不喜欢重新审视同一段代码然后重写其中的一部分呢?不过,这总比从头开始做要好。你知道你同意我的观点。
这次,我们将添加使用所有这些值 else的代码。我们可以参考图来弄清楚我们现在在哪里,以及我们需要解析什么。然后,我们将解析代码添加到与特定状态关联的相应转换下。我刚才写这句话是为了让你感到困惑,但现在让我来展示一下,因为我是一个好人。
我们可以从q0开始。这可能是清零结构的好地方,所以我们会在那里,在case 0下添加代码。之后,根据状态图,有三种可能性:零、一到九,或者一个连字符。你可以在代码中看到表示转换的相关if语句。我们会在这些下面放代码。
case 0:
pinfo->accept = 0;
pinfo->e_count = 0;
pinfo->e_neg = 0;
pinfo->frac_count = 0;
pinfo->neg = 0;
pinfo->overflow = 0;
pinfo->value = 0.0;
if (pinfo->ch == '-') {
// set our negative flag
pinfo->neg = 1;
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 1;
return 1;
}
if (pinfo->ch == '0') {
// do nothing, value is already 0
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 2;
return 1;
}
if (((pinfo->ch >= '1')
&& (pinfo->ch <= '9'))) {
// "parse" our number into value
pinfo->value = pinfo->ch-'0';
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 8;
return 1;
}
goto error;
这个能让我们开始,但我会给你展示另一个,我们在其中进行一些累积。比如q3中的小数部分?为什么不呢?
case 3:
if (((pinfo->ch >= '0')
&& (pinfo->ch <= '9'))) {
// parse the fraction digits (after .)
// we only parse up to 63 because
// a double isn't likely to be
// more precise than that anyway
if(pinfo->frac_count<63) {
cp=pinfo->ch-'0';
if(0!=pinfo->neg)
cp=-cp;
// turn 1-9 into .1-.9 or .01-.09 or whatever
// depending on frac_count. Then add it to
// the result
pinfo->value+=(cp*(pow(10, (pinfo->frac_count * -1))));
// increment the frac_count
++pinfo->frac_count;
}
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 4;
return 1;
}
goto error;
那只是一点点数学。我数学不好,但我通过反复试验得出了这个结果。我有时候有点慢,但我用毅力弥补了。
现在,我们遍历每个状态,并在每个转换下,解析相关部分,根据其他成员的值调整value累加器。在现实世界中,这将是迭代进行的,在你构建每个部分时进行测试,但我真的想要一个蒙太奇,而这是我能做到的最接近的。
为了达到最佳效果,请在查看代码时播放此音乐。
int lexnum(lex_info* pinfo) {
int cp;
if(0!=pinfo->accept && 0>pinfo->ch)
goto accepted;
switch(pinfo->state) {
case 0:
pinfo->accept = 0;
pinfo->e_count = 0;
pinfo->e_neg = 0;
pinfo->frac_count = 0;
pinfo->neg = 0;
pinfo->overflow = 0;
pinfo->value = 0.0;
if (pinfo->ch == '-') {
// set our negative flag
pinfo->neg = 1;
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 1;
return 1;
}
if (pinfo->ch == '0') {
// do nothing, value is already 0
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 2;
return 1;
}
if (((pinfo->ch >= '1')
&& (pinfo->ch <= '9'))) {
// "parse" our number into value
pinfo->value = pinfo->ch-'0';
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 8;
return 1;
}
goto error;
case 1:
if (pinfo->ch == '0') {
// do nothing. value is already 0
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 2;
return 1;
}
if (((pinfo->ch >= '1')
&& (pinfo->ch <= '9'))) {
// "parse" a digit into value
// will always be negative from
// here
pinfo->value = -(pinfo->ch-'0');
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 8;
return 1;
}
goto error;
case 2:
if (pinfo->ch == '.') {
// now increment our frac count
++pinfo->frac_count;
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 3;
return 1;
}
if (((pinfo->ch == 'E')
|| (pinfo->ch == 'e'))) {
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 5;
return 1;
}
pinfo->accept = 1;
return 1; // -1 != pinfo->ch;
case 3:
if (((pinfo->ch >= '0')
&& (pinfo->ch <= '9'))) {
// parse the fraction digits (after .)
// we only parse up to 63 because
// a double isn't likely to be
// more precise than that anyway
if(pinfo->frac_count<63) {
cp=pinfo->ch-'0';
if(0!=pinfo->neg)
cp=-cp;
// turn 1-9 into .1-.9 or .01-.09 or whatever
// depending on frac_count. Then add it to
// the result
pinfo->value+=(cp*(pow(10, (pinfo->frac_count * -1))));
// increment the frac_count
++pinfo->frac_count;
}
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 4;
return 1;
}
goto error;
case 4:
if (((pinfo->ch == 'E')
|| (pinfo->ch == 'e'))) {
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 5;
return 1;
}
if (((pinfo->ch >= '0')
&& (pinfo->ch <= '9'))) {
// we're doing the exact same thing
// here we did in state 3/q3
if(pinfo->frac_count<63) {
cp=pinfo->ch-'0';
if(0!=pinfo->neg)
cp=-cp;
pinfo->value+=(cp*(pow(10, (pinfo->frac_count * -1))));
++pinfo->frac_count;
}
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 4;
return 1;
}
pinfo->accept = 1;
return 1; // -1 != pinfo->ch;
case 5:
if (((pinfo->ch == '+')
|| (pinfo->ch == '-'))) {
if('-'==pinfo->ch) {
// use this to determine E is
// negative instead of positive
pinfo->e_neg = 1;
}
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 6;
return 1;
}
if (((pinfo->ch >= '0')
&& (pinfo->ch <= '9'))) {
cp=pinfo->ch-'0';
// we accept up to SOMETHINGe+1000000
if(pinfo->e_count>1000000) {
// we overflowed
pinfo->overflow = 1;
} else {
// add the next digit to e
pinfo->e_count=pinfo->e_count*10+cp;
}
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 7;
return 1;
}
goto error;
case 6:
if (((pinfo->ch >= '0')
&& (pinfo->ch <= '9'))) {
// same as state 5
cp=pinfo->ch-'0';
if(pinfo->e_count>1000000) {
// we overflowed
pinfo->overflow = 1;
} else {
// add the next digit to e
pinfo->e_count=pinfo->e_count*10+cp;
}
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 7;
return 1;
}
goto error;
case 7:
if (((pinfo->ch >= '0')
&& (pinfo->ch <= '9'))) {
// same as state 5
cp=pinfo->ch-'0';
if(pinfo->e_count>1000000) {
// we overflowed
pinfo->overflow = 1;
} else {
// add the next digit to e
pinfo->e_count=pinfo->e_count*10+cp;
}
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 7;
return 1;
}
pinfo->accept = 1;
return 1; // -1 != pinfo->ch;
case 8:
if (pinfo->ch == '.') {
// increment our frac count
++pinfo->frac_count;
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 3;
return 1;
}
if (((pinfo->ch == 'E')
|| (pinfo->ch == 'e'))) {
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 5;
return 1;
}
if (((pinfo->ch >= '0')
&& (pinfo->ch <= '9'))) {
// "parse" a digit:
cp = pinfo->ch-'0';
if(pinfo->neg)
cp=-cp;
// we have to fudge a little to avoid
// rounding errors
pinfo->value = floor(pinfo->value*10.0+0.5)+cp;
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 8;
return 1;
}
pinfo->accept = 1;
return 1; // -1 != pinfo->ch;
}
error:
pinfo->ch = fgetc(pinfo->pfile);
return 0;
accepted:
// do the final math to fixup the number
if(0<pinfo->e_count) {
double p = pow(10,pinfo->e_count);
if(0!=pinfo->e_neg) {
// it's negative
pinfo->value/=p;
} else {
pinfo->value*=p;
}
}
return 0;
}
我故意将switch语句缩进得不好,这样即使格式不佳,你也可以在这个网站上阅读它,而不会让每一行都换行。我还给协程添加了一个小hack,在它运行状态机之前,它会检查是否已到达输入末尾,并且是否已接受。如果是,它会跳转到accepted:,在那里它会完成数字计算。为了方便起见,我还让接受状态始终返回1,而不是仅在未到达EOF时返回1。这样做的结果是,你最后一次调用lexnum()时,最终的数字将被计算出来。这个hack只在词法分析器可以使用EOF作为结束条件的情况下才有效。大多数现实世界的词法分析例程必须支持至少一些其他类型的结束条件。通常发生的情况是,一旦它无法沿着图中的黑色箭头移动,它就会停止。那就是结束条件。这有点宽松,因为它意味着3.14x5将在“x”之前停止并获得有效结果,但我们喜欢宽松,因为它只是另一种表达灵活(道德上或非道德上)的方式,对吧?不过,为了演示,我没有这样做,因为那样我们就必须在驱动代码中处理它,而它会增加复杂性而没有说明性。代码已经足够复杂了。
现在运行时,我们得到这个
3.141592653589793238462643 Accepted number: 3.141593
它还会适当地拒绝无效数字。
至此,我们完成了我们设定的目标,也就是说,通过采取可疑的做法来完成一项价值微薄的任务。
如何使用正则表达式
首先,不要把它当作动词。我这么做是因为我有点叛逆。总之,正则表达式只是定义文本模式的缩写操作。我们将介绍非回溯正则表达式,因为它比另一种选择更有用,而且更简单。这一切都始于一些核心运算符。
核心运算符
(abc)- 子表达式。它的工作方式与任何语言中的一样,即它会覆盖优先级。捕获匹配也使用括号来指定要捕获的文本部分,但不要担心,因为捕获是附加功能,不是核心正则表达式的一部分。abc- 连接。匹配“abc”,或者依次匹配a、b,然后是c。你会注意到它没有运算符。它是隐式的。a|b|c- 交替。匹配a或b或c。|的优先级使得abc|def|ghi按预期工作,即它匹配“abc”、“def”或“ghi”。(abc)?- 将左边的表达式匹配零次或一次。这里,它匹配“abc”零次或一次。注意我们需要括号,因为通常由于运算符优先级,?只匹配其左边的字符。(abc)*- Kleene星号。匹配“abc”零次或多次。有效字符串包括“”、“abc”、“abcabc”和“abcabcabcabcabc”。
像任何语言中的运算符一样,它们是组合的——你将它们用作更大表达式的构建块,这些表达式也使用它们,以此类推。还有一些常见的运算符,是上述运算符的简写。
常见语法糖
[a-c]- 匹配一个字符集。前面的匹配一个字符,该字符可以是a,或b,或c。它也可以写成[abc]。长写法是(a|b|c)。[^a-c]- 匹配任何一个不是a、b或c的字符。长写法太长,无法在此处写出,但它会像(d|e|f|g|...)以及所有控制字符、数字和符号——除了a、b或c之外的一切。(abc)+- 将表达式匹配一次或多次。这将匹配“abc”或“abcabc”,但不匹配“”。其长写法是(abc)(abc)*。
结论
我不想让你一无所获,所以我希望我已经传达了几个想法。
- 正则表达式是一种简单、不吓人、函数式的编程语言,其输出是一个DFA状态机。
- 因此,它们可以用来匹配文本,或者生成运行DFA状态机的代码。
- 生成正则表达式状态机的代码可以通过状态图来创建文档,这可以弥补生成代码的丑陋。
- 让计算机生成复杂的代码可能不会为你节省前期工作,但它会在后期带来巨大的回报,通过减少bug和简化测试。例如,我们可以相当确信状态机将拒绝不匹配我们初始正则表达式的字符串,而无需测试所有这些情况。
- 为了使其再次有用,滥用旧代码是可以接受的。
- 你的电脑基本上是愚钝的,但很积极。如果你为了方便起见而抛弃你的原则,你可以哄它做一些它本来绝不会同意的事情。
历史
- 2020年1月2日 - 初始提交
