人工神经网络 C++ 类
4.99/5 (71投票s)
人工神经网络 C++ 类,包含两个用例:计数器和手写数字识别。
- 下载 NeuralNetwork 类源代码文件 - 3 KB
- 下载 CounterNeuralNetwork 源代码文件 - 6 KB
- 下载 DigitsNeuralNetwork 源代码文件 - 117 KB
目录
背景
本文不是为了解释(ANN)人工神经网络的科学原理。它提供了一个简单的 C++ 类,没有任何复杂的数学计算的反向传播算法。如果您对 ANN 有丰富的经验,可以跳到下一节,否则,您可以回顾一下这些关于 ANN 的非常好的资源。我提供了两个用例,以尽可能地方便代码使用。
引言
如今,(ANN)人工神经网络已在生活的许多领域占据主导地位,无论是在工业还是家庭。ANN 使机器能够学习并模拟人脑以识别模式、做出预测以及解决每个业务部门的问题。我们日常使用的智能手机和计算机在某些应用中都使用 ANN。例如,智能手机和计算机中的指纹和面部解锁服务使用 ANN。手写签名验证使用 ANN。我编写了一个简单的人工神经网络 C++ 类实现,该类处理反向传播算法。代码依赖于Eigen开源模板来处理矩阵数学。我使代码尽可能简单和快速。
NeuralNetwork 类
NeuralNetwork 是一个简单的 C++ 类,具有以下结构
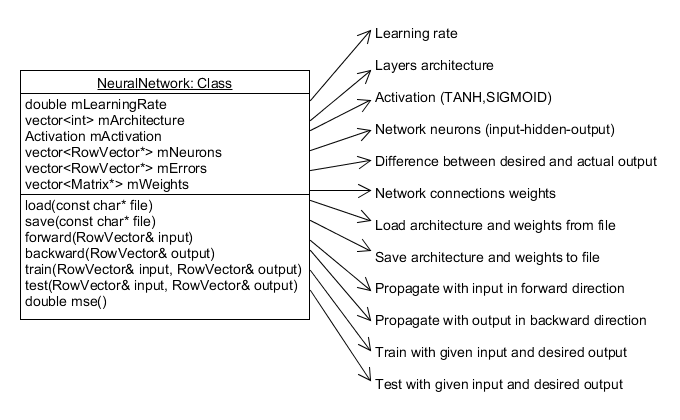
代码使用 Eigen 模板库中的 RowVectorXd 和 MatrixXd。主要函数 "train" 和 "test" 以 RowVector 格式接收输入和期望输出。它们都调用 "forward" 函数,该函数使用向量乘法。

前向传播
void NeuralNetwork::forward(RowVector& input) {
// set first layer input
mNeurons.front()->block(0, 0, 1, input.size()) = input;
// propagate forward (vector multiplication)
for (unsigned int i = 1; i < mArchitecture.size(); i++) {
// copy values ingoring last neuron as it is a bias
mNeurons[i]->block(0, 0, 1, mArchitecture[i]) =
(*mNeurons[i - 1] * *mWeights[i - 1]).block(0, 0, 1, mArchitecture[i]);
for (int col = 0; col < mArchitecture[i]; col++)
mNeurons[i]->coeffRef(col) = activation(mNeurons[i]->coeffRef(col));
}
}
该函数将输入传播通过网络层以获得最后一层的输出。隐藏层中的每个神经元首先计算其输入的加权总和。然后,它将一个激活函数(sigmoid)应用于该总和以得出其输出。此函数仅影响神经元的值。它不影响连接权重或误差。此函数通过向量乘法进行此求和。
(*mNeurons[i - 1] * *mWeights[i - 1])
然后,将结果值通过activation函数。
double NeuralNetwork::activation(double x) {
if (mActivation == TANH)
return tanh(x);
if (mActivation == SIGMOID)
return 1.0 / (1.0 + exp(-x));
return 0;
}
tanh

sigmoid

反向传播
void NeuralNetwork::backward(RowVector& output) {
// calculate last layer errors
*mErrors.back() = output - *mNeurons.back();
// calculate hidden layers' errors (vector multiplication)
for (size_t i = mErrors.size() - 2; i > 0; i--)
*mErrors[i] = *mErrors[i + 1] * mWeights[i]->transpose();
// update weights
size_t size = mWeights.size();
for (size_t i = 0; i < size; i++)
for (int col = 0, cols = (int)mWeights[i]->cols(); col < cols; col++)
for (int row = 0; row < mWeights[i]->rows(); row++) {
mWeights[i]->coeffRef(row, col) +=
mLearningRate *
mErrors[i + 1]->coeffRef(col) *
activationDerivative(mNeurons[i + 1]->coeffRef(col)) *
mNeurons[i]->coeffRef(row);
}
}
该函数是反向传播算法的关键。它获取最后一层的输出,然后向后传播通过网络层,计算每一层的误差,并根据规则更新连接权重。
新权重 = 旧权重 + 学习率 * 下一层误差 * sigmoidDerivative(下一神经元值)
double NeuralNetwork::activationDerivative(double x) {
if (mActivation == TANH)
return 1 - tanh(x) * tanh(x);
if (mActivation == SIGMOID)
return x * (1.0 - x);
return 0;
}
tanh导数

sigmoid导数

注意:sigmoidDerivative 的曲线具有重要的意义。由于其输入范围从 0 到 1(神经元值),因此有三种可能的情况:
- 神经元值接近
0,因此权重值不需要支持。
- 神经元值接近
0.5,因此权重值需要进行微小的更改。
- 神经元值接近
1,因此权重值不需要支持。
训练
void NeuralNetwork::train(RowVector& input, RowVector& output) {
forward(input);
backward(output);
}
该函数在前向方向传播输入,然后将结果输出反向传播以调整连接权重。
测试
void NeuralNetwork::test(RowVector& input, RowVector& output) {
forward(input);
// calculate last layer errors
*mErrors.back() = output - *mNeurons.back();
}
该函数在前向方向传播输入,然后计算结果输出和期望输出之间的误差。
评估
评估神经网络模型的性能有多种方法,例如混淆矩阵、准确率、精确率、召回率和F1 分数。我在代码中通过在每次测试调用后调用 evaluate 函数来添加“混淆矩阵”的计算。
void NeuralNetwork::evaluate(RowVector& output) {
double desired = 0, actual = 0;
mConfusion->coeffRef(
vote(output, desired),
vote(*mNeurons.back(), actual)
)++;
}
此函数根据实际输出和期望输出之间的匹配情况,简单地填充混淆矩阵中的相应单元格。
完成所有测试后,混淆矩阵可用于计算精确率、召回率和 F1 分数。
void NeuralNetwork::confusionMatrix(RowVector*& precision, RowVector*& recall) {
int rows = (int)mConfusion->rows();
int cols = (int)mConfusion->cols();
precision = new RowVector(cols);
for (int col = 0; col < cols; col++) {
double colSum = 0;
for (int row = 0; row < rows; row++)
colSum += mConfusion->coeffRef(row, col);
precision->coeffRef(col) = mConfusion->coeffRef(col, col) / colSum;
}
recall = new RowVector(rows);
for (int row = 0; row < rows; row++) {
double rowSum = 0;
for (int col = 0; col < cols; col++)
rowSum += mConfusion->coeffRef(row, col);
recall->coeffRef(row) = mConfusion->coeffRef(row, row) / rowSum;
}
...
}
这种计算将在第二个用例 手写数字识别 中得到清晰说明。
用例
简单的计数器

神经网络接收二进制输入(3 位)并生成等于输入 + 1 的输出。然后将输出作为输入反馈回网络。如果输入数字等于 7(二进制的 111),则输出应为 0。使用反向传播算法训练网络以调整网络连接权重。训练过程大约需要 2 分钟来最小化期望输出和实际网络输出之间的误差。
| 输入 | 输出 |
| 0 0 0 | 0 0 1 |
| 0 0 1 | 0 1 0 |
| 0 1 0 | 0 1 1 |
| 0 1 1 | 1 0 0 |
| 1 0 0 | 1 0 1 |
| 1 0 1 | 1 1 0 |
| 1 1 0 | 1 1 1 |
| 1 1 1 | 0 0 0 |

只需使用所需的架构和learningRate构建 NeuralNetwork 类。
NeuralNetwork net({ 3, 5, 3 }, 0.05, NeuralNetwork::Activation::TANH);
输入层 3 个神经元,隐藏层 5 个神经元,输出层 3 个神经元。
0.05 的学习率。
下图描述了使用 50,000 次试验的网络完整训练过程。

训练网络
void train(NeuralNetwork& net) {
cout << "Training:" << endl;
RowVector input(3), output(3);
int stop = 0;
for (int i = 0; stop < 8 && i < 50000; i++) {
cout << i + 1 << endl;
for (int num = 0; stop < 8 && num < 8; num++) {
input.coeffRef(0) = (num >> 2) & 1;
input.coeffRef(1) = (num >> 1) & 1;
input.coeffRef(2) = num & 1;
output.coeffRef(0) = ((num + 1) >> 2) & 1;
output.coeffRef(1) = ((num + 1) >> 1) & 1;
output.coeffRef(2) = (num + 1) & 1;
net.train(input, output);
double mse = net.mse();
cout << "In [" << input << "] "
<< " Desired [" << output << "] "
<< " Out [" << net.mNeurons.back()->unaryExpr(ptr_fun(unary)) << "] "
<< " MSE [" << mse << "]" << endl;
stop = mse < 0.1 ? stop + 1 : 0;
}
}
}
该函数接收一个架构为 { 3, 5, 3 } 的网络,并进行 50000x8 次训练调用,直到达到可接受的误差范围。每次训练调用后,它会显示输入、输出和期望输出。
- 在训练的早期阶段,均方误差 (MSE) 很大,输出与期望输出相差甚远。

- 经过多次训练后,MSE 减小,输出更接近期望输出。

- 最终,经过 788 次迭代,MSE 小于 0.1,输出接近期望输出。

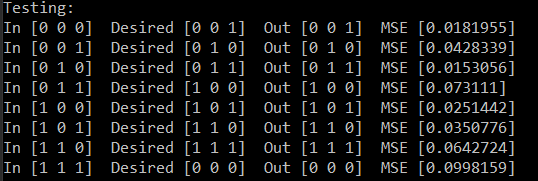
测试网络
void test(NeuralNetwork& net) {
cout << "Testing:" << endl;
RowVector input(3), output(3);
for (int num = 0; num < 8; num++) {
input.coeffRef(0) = (num >> 2) & 1;
input.coeffRef(1) = (num >> 1) & 1;
input.coeffRef(2) = num & 1;
output.coeffRef(0) = ((num + 1) >> 2) & 1;
output.coeffRef(1) = ((num + 1) >> 1) & 1;
output.coeffRef(2) = (num + 1) & 1;
net.test(input, output);
double mse = net.mse();
cout << "In [" << input << "] "
<< " Desired [" << output << "] "
<< " Out [" << net.mNeurons.back()->unaryExpr(ptr_fun(unary)) << "] "
<< " MSE [" << mse << "]" << endl;
}
}
此函数使用预训练网络测试一些输入。它会打印输出结果和 MSE。
保存网络
int main() {
NeuralNetwork net({ 3, 5, 3 }, 0.05);
RowVector input(3), output(3);
train(net, input, output);
test(net, input, output);
net.save("params.txt"); // Save architecture and weights
return 0;
}
在训练和测试网络后,我们可以将网络结构保存在文件中,以便以后加载使用,而无需重新训练。
在我们的例子中,结果文件包含
learningRate: 0.05
architecture: 3,5,3
activation: 0
weights:
-1.34013 0.811848 0.314629 1.85447 -0.343212 0.151176
0.98971 -0.684254 1.20649 0.260128 -6.50245 -2.31706
0.702027 -3.15824 -0.80735 1.07841 -2.57619 -2.17761
0.13025 3.17894 0.594173 -3.18092 -0.0574412 -2.39394,
-2.67379 0.467493 0.403606
-1.22918 1.67581 1.60877
1.1605 -1.95284 0.942444
-1.92978 -0.704029 -1.12284
-1.34765 -2.8206 1.44205
-0.996246 -1.52939 0.205469
权重部分的第一行表示输入层第一个神经元与下一层所有神经元之间的权重。
-1.34013 0.811848 0.314629 1.85447 -0.343212 0.151176

权重部分的第二行表示输入层第二个神经元与下一层所有神经元之间的权重。
0.98971 -0.684254 1.20649 0.260128 -6.50245 -2.31706

以此类推...
手写数字识别
手写识别是人工神经网络最成功的应用之一。它是神经网络学习的“Hello world”应用程序。在之前的用例中,我使用了一个浅层神经网络,它有三层神经元来处理输入并生成输出。浅层神经网络可以处理同样复杂的任务。但是在手写识别中,我们需要更高的准确性和非线性。因此,我必须使用深度神经网络(DNN)。DNN 有两个或更多隐藏层的神经元来处理输入。
网络架构
使用网络架构 {784, 64, 16, 10}(输入 - 两个隐藏层 - 输出),我取得了 93.16% 的成功率。

活动图
下图说明了整个过程的活动图。

使用的库
本项目使用
- MNIST 数据集用于网络训练和测试。您需要下载 MNIST 数据集文件并将其放在项目执行路径中。
- libpng 库用于读取 PNG 文件。您可以下载 libpng16(lib - h)文件并将其放在项目构建路径中。
- zlib 库由 libpng16 内部使用以解压缩图像。
MNIST 数据集包含 60,000 张手写数字(从零到九)的训练图像和 10,000 张测试图像。因此,MNIST 数据集有 10 个不同的类别。手写数字图像表示为 28×28 的矩阵,其中每个单元格包含灰度像素值(0 到 1)。

训练与测试
在训练和测试过程中,数字从其 PNG 文件中读取,并从 28x28 图像转换为 784 个灰度双精度值。该向量代表神经网络输入层的输入。
void readPng(const char* filepath, RowVector*& data) {
pngwriter image;
image.readfromfile(filepath);
int width = image.getwidth(); // 28
int height = image.getheight(); // 28
data = new RowVector(width * height); // 784
for (int y = 0; y < height; y++)
for (int x = 0; x < width; x++)
data->coeffRef(0, y * width + x) = image.dread(x, y);
}

下图描述了使用 60,000 张图像(50,000 张训练 - 10,000 张测试)的网络完整训练和测试过程。

- 在训练的早期阶段,误差很大,输出与期望输出相差甚远。
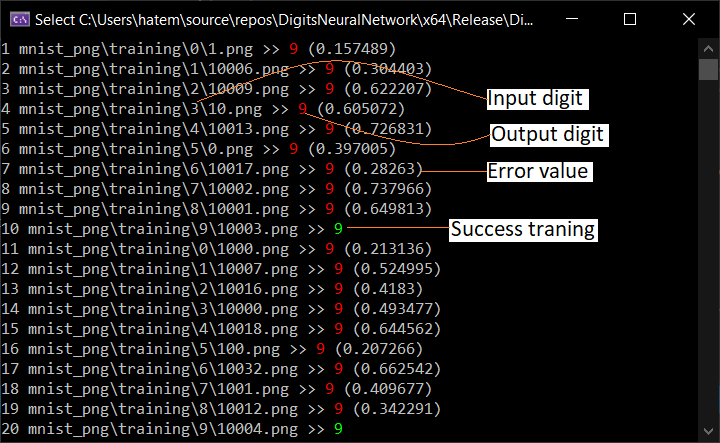
- 经过多次训练后,MSE 减小,输出更接近期望输出。

- 测试 10000 张图像后

- 显示训练和测试成本以及错误率

保存网络
int main() {
.......
if (!testOnly)
net.save("params.txt");
return 0;
}
在训练和测试网络后,我们可以将网络结构保存在文件中,以便以后加载使用,而无需重新训练。如果要重新训练,则必须删除构建路径中的“params.txt”文件。
在我们的例子中,结果文件包含
learningRate: 0.05
architecture: 784,64,16,10
activation: 1
weights:
-0.997497 -0.307718 -0.0558184 0.124485 -0.188635 0.557909 0.242286
-0.898618 -0.942442 0.355693 0.284951 0.100192 0.724357 -0.998474
0.763909 -0.127537 0.893246 -0.956969 -0.492111 -0.775506 -0.603442
-0.907712 -0.987793 -0.0556963 -0.510117 0.450484 0.644276 0.951292
0.105869 -0.76458 0.586596 0.480819 0.253029 -0.672964 -0.418134
0.117222 0.121494 0.439985 -0.459639 -0.514145 0.458296 0.639027
-0.926817 -0.581164 0.774529 -0.392315 -0.985656 0.405133 -0.0527665
-0.0163884 -0.00704978 0.138768 -0.2219 -0.927671 -0.880856 0.977355
-0.927854 0.253273 -0.154149 -0.877621 0.797845 0.388653 0.0682699
0.3361 -0.108066
0.127171 -0.962889 0.39848 -0.457381 0.470931 -0.574816 -0.820429
-0.851558 -0.925108 0.224769 0.575488 0.975402 -0.688955 0.78692
0.0274972 -0.218848 -0.790765 0.708121 0.144139 -0.574694 0.749809
0.781732 0.362285 -0.662099 -0.903134 0.375225 0.581286 -0.679678
0.0863369 0.295511 -0.418195 0.241249 -0.720573 -0.794733 0.0434278
-0.81109 0.895749 0.652699 0.970824 0.643422 -0.0625935 0.776421
-0.656117 0.23075 -0.18247 -0.250649 -0.197546 0.621632 0.804376
-0.976745 0.178747 0.137059 -0.404828 -0.564013 -0.309915 -0.376385
-0.66924 0.245216 -0.3961 0.160741 0.364788 0.150121 -0.811396
-0.837397 -0.901669
....
评估
测试网络后,我们可以从混淆矩阵中计算出精确率、召回率和 F1 分数等评估项。
精确率是正确识别(真正例)与预测数字的比例。
Precision = (0.95+0.97+0.95+0.95+0.92+0.93+0.96+0.95+0.94+0.89)/10 = 94%
召回率是正确识别(真正例)与实际数字的比例。
Recall = (0.98+0.98+0.93+0.93+0.92+0.94+0.93+0.94+0.92+0.92)/10 = 94%
void evaluate(NeuralNetwork& net) {
RowVector* precision, * recall;
net.confusionMatrix(precision, recall);
double precisionVal = precision->sum() / precision->cols();
double recallVal = recall->sum() / recall->cols();
double f1score = 2 * precisionVal * recallVal / (precisionVal + recallVal);
cout << "Confusion matrix:" << endl;
cout << *net.mConfusion << endl;
cout << "Precision: " << (int)(precisionVal * 100) << '%' << endl;
cout << *precision << endl;
cout << "Recall: " << (int)(recallVal * 100) << '%' << endl;
cout << *recall << endl;
cout << "F1 score: " << (int)(f1score * 100) << '%' << endl;
delete precision;
delete recall;
}
结果值如下所示
Confusion matrix:
98.6735 0.102041 0 0.102041 0 0.204082 0.306122 0.306122 0.306122 0
5.659e-313 98.2379 0.264317 0.176211 0 0 0.264317 0.176211 0.792952 0.0881057
1.06589 0.290698 93.5078 0.387597 1.45349 0.290698 0.484496 1.16279 0.968992 0.387597
0 0.29703 1.18812 93.5644 0.0990099 1.48515 0.29703 0.990099 0.891089 1.18812
0.101833 0 0.407332 0.101833 92.9735 0 0.916497 0.203666 0 5.29532
0.44843 0.112108 0.112108 2.01794 0.336323 94.2825 0.44843 0.560538 1.00897 0.672646
1.46138 0.313152 0.417537 0 1.04384 2.71399 93.6326 0.104384 0.313152 0
0 1.07004 1.16732 0.194553 0.583658 0.194553 0 94.5525 0.0972763 2.14008
0.616016 0.513347 0.616016 1.12936 1.12936 0.718686 0.821355 0.821355 92.4025 1.23203
0.99108 0.396432 0 0.891972 3.07235 0.396432 0.099108 0.693756 0.49554 92.9633
Precision: 94%
0.95459 0.972949 0.958292 0.951662 0.922222 0.934444 0.961415 0.951076 0.948367 0.895893
Recall: 94%
0.986735 0.982379 0.935078 0.935644 0.929735 0.942825 0.936326 0.945525 0.924025 0.929633
F1 score: 94%
我们可以在下表中可视化混淆矩阵

此表显示了模型将每个数字正确分类的次数(蓝色),以及该标签最常被混淆为哪些数字(灰色)。
历史
- 2021 年 1 月 24 日:初始发布
- 2021 年 3 月 7 日:使用混淆矩阵评估模型
