在 Python 中构建森林系列:单向二叉搜索树
4.43/5 (3投票s)
使用 Python 构建线程二叉搜索树。
引言
本文是“Python 系列:构建森林”系列的第三篇文章。在上篇文章《Python 系列:二叉树遍历》中,我们讨论了使用递归和辅助栈来实现二叉树的遍历。本文将构建二叉搜索树的一个变种——线索二叉搜索树。线索二叉搜索树利用空指针(左或右子节点为空)的属性来实现某些特定顺序的遍历,而无需使用栈或递归。
项目设置
与“Python 系列:构建二叉搜索树”系列中的其他文章一样,本文的实现假定使用 Python 3.9 或更高版本。本文为我们的项目增加了两个模块:用于线索二叉搜索树实现的 `single_threaded_binary_trees.py` 和用于单元测试的 `test_single_threaded_binary_trees.py`。添加这两个文件后,我们的项目结构如下:
forest-python
├── forest
│ ├── __init__.py
│ ├── binary_trees
│ │ ├── __init__.py
│ │ ├── binary_search_tree.py
│ │ ├── single_threaded_binary_trees.py
│ │ └── traversal.py
│ └── tree_exceptions.py
└── tests
├── __init__.py
├── conftest.py
├── test_binary_search_tree.py
├── test_single_threaded_binary_trees.py
└── test_traversal.py
(完整代码可在 forest-python 获取。)
什么是线索二叉树?
线索二叉树是二叉树的一种变种,它通过利用节点的空左指针或右指针来优化特定顺序的遍历。线索二叉树有两种类型:
- 单线索二叉树 (Single-threaded binary tree):对于节点中空的左指针或右指针,它会被“线索化”,指向该节点的中序前驱或后继。换句话说,左指针或右指针不再为空,而是指向节点的(前驱或后继)。单线索二叉树有两种实现方式:左单线索二叉树和右单线索二叉树。
- 右单线索二叉树 (Right single-threaded binary tree):节点的空右指针指向该节点的后继,如果节点有空的左指针,则该指针保持为空。
- 左单线索二叉树 (Left single-threaded binary tree):节点的空左指针指向该节点的前驱,如果节点有空的右指针,则该指针保持为空。
- 双线索二叉树 (Double-threaded binary tree):对于任何空的左指针或右指针,这些空指针都会被线索化,指向中序前驱或后继:如果左指针为空,则指向前驱;如果右指针为空,则指向后继。
虽然线索可以添加到任何二叉树中,但最适合将其添加到二叉搜索树或其变种(即满足二叉搜索树性质的树)中。因此,在本项目中,我们将实现的线索二叉树是带有线索的二叉搜索树(即线索二叉搜索树)。在文章的其余部分,为了避免术语冗余,我们提及的线索二叉树都将特指二叉搜索树。
此外,线索不一定需要指向中序前驱或后继,也可以指向前序或后序。但是,中序是二叉搜索树的有序序列,所以指向中序前驱或后继的线索是最常见的。
我们为什么需要线索?
为二叉树添加线索会增加复杂性,那么我们为什么需要线索呢?有几个原因:
- 快速访问后继或前驱
- 某些遍历方式无需辅助栈或递归
- 由于无需辅助栈或递归,减少了执行遍历时的内存消耗
- 利用了被浪费的空间。由于节点中空的左指针或右指针不存储任何信息,我们可以将其用作线索。
对于每种类型的线索二叉树,我们可以总结添加线索的好处如下:
- 右单线索二叉树无需栈或递归即可执行中序和前序遍历。它还提供了快速访问后继的功能。
- 左单线索二叉树无需栈或递归即可执行反中序遍历,并提供快速访问前驱的功能。
- 双线索二叉树兼具两种单线索二叉树的优点。
构建单线索二叉搜索树
正如我们在“构建二叉搜索树”部分所做的那样,本节将逐步介绍实现过程,并讨论一些实现选择背后的想法。
节点
节点结构与二叉搜索树节点类似,但增加了一个额外的字段 `is_thread`。`is_thread` 属性的目的是区分左指针或右指针是普通指针还是线索。

`is_thread` 属性是一个布尔变量:如果该指针(根据单线索二叉树的类型,为左指针或右指针)是线索,则为 `True`;否则为 `False`。
@dataclasses.dataclass
class Node:
key: Any
data: Any
left: Optional["Node"] = None
right: Optional["Node"] = None
parent: Optional["Node"] = None
is_thread: bool = False
与二叉搜索树节点一样,我们将线索二叉树的节点类定义为数据类 (dataclass)。
右单线索二叉搜索树
顾名思义,我们可以通过下图来形象地理解右单线索二叉树:
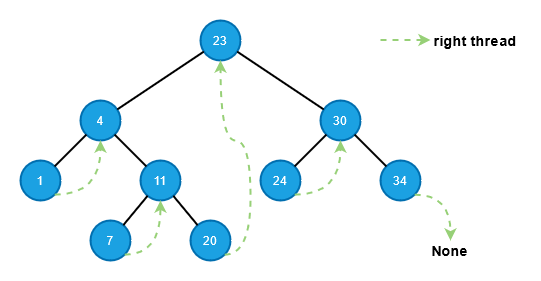
每个节点的空右指针都指向其中序后继,并且其 `is_thread` 变量设置为 `True`,除了最右边的节点。最右边节点的右指针仍然为空,其 `is_thread` 为 `False`,这样我们就知道它是最右边的节点(即没有后继了)。
与二叉搜索树一样,右单线索二叉树也拥有核心功能(`insert`、`delete` 和 `search`)用于构建和修改,以及其他不与特定树绑定的辅助功能,例如获取最左节点和获取树的高度。我们在二叉搜索树中实现的 `__repr__()` 函数也可以用于调试目的。
这里的主要区别在于,我们实现了无需栈或递归即可进行中序和前序遍历的方法。
class RightThreadedBinaryTree:
def __init__(self) -> None:
self.root: Optional[Node] = None
def __repr__(self) -> str:
"""Provie the tree representation to visualize its layout."""
if self.root:
return (
f"{type(self)}, root={self.root}, "
f"tree_height={str(self.get_height(self.root))}"
)
return "empty tree"
def search(self, key: Any) -> Optional[Node]:
…
def insert(self, key: Any, data: Any) -> None:
…
def delete(self, key: Any) -> None:
…
@staticmethod
def get_leftmost(node: Node) -> Node:
…
@staticmethod
def get_rightmost(node: Node) -> Node:
…
@staticmethod
def get_successor(node: Node) -> Optional[Node]:
…
@staticmethod
def get_predecessor(node: Node) -> Optional[Node]:
…
@staticmethod
def get_height(node: Optional[Node]) -> int:
…
def inorder_traverse(self) -> traversal.Pairs:
…
def preorder_traverse(self) -> traversal.Pairs:
…
Insert
`insert` 操作类似于二叉搜索树的插入。区别在于线索二叉树需要考虑线索的更新。因此,插入步骤如下:
- 通过从根节点开始遍历树,并将新节点键与沿途每个节点的键进行比较,找到插入新节点的合适位置(即新节点的父节点)。向右子树遍历时,还要检查 `is_thread` 变量。如果该变量为 `True`,则表示我们已到达叶子节点,该叶子节点就是新节点的父节点。
- 更新新节点的 parent 属性以指向父节点。
- 如果新节点是父节点的左子节点,则将新节点的右指针指向父节点,并将 `is_thread` 变量设置为 `True`。更新父节点的左指针指向新节点。
- 如果新节点是其父节点的右子节点,则将父节点的右指针(在插入之前,父节点的右指针必须是线索)复制到新节点的右指针,并将 `is_thread` 变量设置为 `True`。更新父节点的右指针指向新节点,并将父节点的 `is_thread` 设置为 `False`。
下图演示了节点插入的步骤。

我们可以按以下方式实现插入:
def insert(self, key: Any, data: Any) -> None:
new_node = Node(key=key, data=data)
parent: Optional[Node] = None
current: Optional[Node] = self.root
while current:
parent = current
if new_node.key < current.key:
current = current.left
elif new_node.key > current.key:
# If the node is thread, meaning it's a leaf node.
if current.is_thread:
current = None
else:
current = current.right
else:
raise tree_exceptions.DuplicateKeyError(key=new_node.key)
new_node.parent = parent
# If the tree is empty
if parent is None:
self.root = new_node
elif new_node.key < parent.key:
parent.left = new_node
# Update thread
new_node.right = parent
new_node.is_thread = True
else:
# Update thread
new_node.is_thread = parent.is_thread
new_node.right = parent.right
parent.is_thread = False
# Parent's right must be set after thread update
parent.right = new_node
搜索
搜索操作也类似于二叉搜索树的搜索,但需要检查 `is_thread` 变量来确定我们是否到达了叶子节点。
- 从根节点开始遍历树,并将要查找的键与沿途每个节点的键进行比较。
- 如果键匹配,则找到了该节点。
- 如果在到达叶子节点后(如果 `is_thread` 为 `True`,则表示该节点是叶子节点)仍未找到匹配的键,则表示该键不存在于树中。
实现与我们在二叉搜索树中进行的实现相似,只需进行一个简单的修改——检查 `is_thread`。
def search(self, key: Any) -> Optional[Node]:
current = self.root
while current:
if key == current.key:
return current
elif key < current.key:
current = current.left
else: # key > current.key
if current.is_thread:
break
current = current.right
return None
删除
与二叉搜索树一样,要删除的右单线索二叉树节点有三种情况:无子节点、只有一个子节点、有两个子节点。我们还使用在“Python 系列:二叉搜索树 - 删除”中使用的替换(transplant)技术来用要删除的节点替换子树。虽然基本思想相同,但 `transplant` 函数和 `delete` 函数都需要考虑右线索。我们最需要记住的是,在删除节点时,如果其他节点的右指针指向要删除的节点,我们需要更新该节点的线索(即右指针)。
情况 1:无子节点
如果待删除节点没有子节点,则其左指针为空,`is_thread` 为 `True`。关于线索,我们需要考虑两种情况。请看下图:

情况 2a:只有一个左子节点
如果待删除节点只有一个左子节点,这意味着节点的 `is_thread` 为 `True`。(例外情况是当待删除节点是根节点且只有一个左子节点时;在这种情况下,节点的 `is_thread` 为 `False` 且其右指针为 `None`)。需要更新线索的情况如下图所示:

情况 2b:只有一个右子节点
如果待删除节点只有一个右子节点,这意味着节点的左指针为空,`is_thread` 为 `False`。由于待删除节点没有左子节点,这意味着没有人指向该节点。

情况 3:有两个子节点
与二叉搜索树的删除类似,待删除节点有两个子节点的情况可以分解为两种子情况:
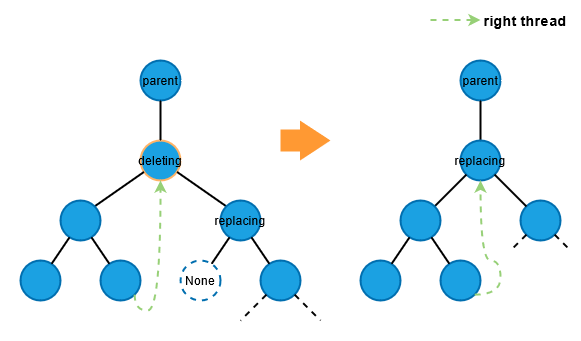
3.a 要删除节点的右子节点也是右子树中最左边的节点。
在这种情况下,右子节点必须只有一个右子节点。因此,我们可以用右子节点替换被删除的节点,如下图所示:
3.b 要删除节点的右子节点也有两个子节点。
在这种情况下,我们从右子树中找到最左边的节点来替换被删除的节点。请注意,当我们从右子树中移除最左边的节点时,它也属于删除情况:情况 1(无子节点)或情况 2(只有一个右子节点)。否则,它就不可能是最左边的节点。
因此,我们两次使用 `transplant` 函数:一次移除最左边的节点,另一次用原来的最左边的节点替换被删除的节点。下图演示了在执行删除时需要考虑线索的情况。
被替换节点没有子节点

被替换节点只有一个右子节点:

根据上图,我们可以实现 `delete` 和 `transplant` 函数如下:
def delete(self, key: Any) -> None:
if self.root and (deleting_node := self.search(key=key)):
# Case 1: no child
if deleting_node.left is None and (
deleting_node.right is None or deleting_node.is_thread
):
self._transplant(deleting_node=deleting_node, replacing_node=None)
# Case 2a: only one left child
elif deleting_node.left and (
deleting_node.is_thread or deleting_node.right is None
# deleting_node.right is None means the deleting node is the root.
):
predecessor = self.get_predecessor(node=deleting_node)
if predecessor:
predecessor.right = deleting_node.right
self._transplant(
deleting_node=deleting_node, replacing_node=deleting_node.left
)
# Case 2b: only one right child
elif deleting_node.left is None and deleting_node.is_thread is False:
self._transplant(
deleting_node=deleting_node, replacing_node=deleting_node.right
)
# Case 3: two children
elif (
deleting_node.left
and deleting_node.right
and deleting_node.is_thread is False
):
predecessor = self.get_predecessor(node=deleting_node)
replacing_node: Node = self.get_leftmost(node=deleting_node.right)
# the leftmost node is not the direct child of the deleting node
if replacing_node.parent != deleting_node:
if replacing_node.is_thread:
self._transplant(
deleting_node=replacing_node, replacing_node=None
)
else:
self._transplant(
deleting_node=replacing_node,
replacing_node=replacing_node.right,
)
replacing_node.right = deleting_node.right
replacing_node.right.parent = replacing_node
replacing_node.is_thread = False
self._transplant(
deleting_node=deleting_node, replacing_node=replacing_node
)
replacing_node.left = deleting_node.left
replacing_node.left.parent = replacing_node
if predecessor and predecessor.is_thread:
predecessor.right = replacing_node
else:
raise RuntimeError("Invalid case. Should never happened")
def _transplant(self, deleting_node: Node, replacing_node: Optional[Node]) -> None:
if deleting_node.parent is None:
self.root = replacing_node
if self.root:
self.root.is_thread = False
elif deleting_node == deleting_node.parent.left:
deleting_node.parent.left = replacing_node
if replacing_node:
if deleting_node.is_thread:
if replacing_node.is_thread:
replacing_node.right = replacing_node.right
else: # deleting_node == deleting_node.parent.right
deleting_node.parent.right = replacing_node
if replacing_node:
if deleting_node.is_thread:
if replacing_node.is_thread:
replacing_node.right = replacing_node.right
else:
deleting_node.parent.right = deleting_node.right
deleting_node.parent.is_thread = True
if replacing_node:
replacing_node.parent = deleting_node.parent
获取高度
要计算线索二叉树的高度,我们可以像在二叉搜索树中那样,递归地为每个子节点的高度加一。如果一个节点有两个子节点,我们使用 max 函数获取子节点中较高的那个高度,然后加一。主要区别在于我们使用 `is_thread` 来检查一个节点是否有右子节点。
@staticmethod
def get_height(node: Optional[Node]) -> int:
if node:
if node.left and node.is_thread is False:
return (
max(
RightThreadedBinaryTree.get_height(node.left),
RightThreadedBinaryTree.get_height(node.right),
)
+ 1
)
if node.left:
return RightThreadedBinaryTree.get_height(node=node.left) + 1
if node.is_thread is False:
return RightThreadedBinaryTree.get_height(node=node.right) + 1
return 0
获取最左侧和最右侧节点
获取最左节点和最右节点的实现与二叉搜索树的实现类似。要获取最右节点,除了检查右指针是否为空外,我们还需要检查 `is_thread` 是否为 `True`。因此,我们可以修改 `get_rightmost` 函数如下:
@staticmethod
def get_rightmost(node: Node) -> Node:
current_node = node
while current_node.is_thread is False and current_node.right:
current_node = current_node.right
return current_node
`get_leftmost` 的实现与二叉搜索树中的 `get_leftmost` 完全相同。
@staticmethod
def get_leftmost(node: Node) -> Node:
current_node = node
while current_node.left:
current_node = current_node.left
return current_node
前驱和后继
由于右单线索二叉树提供快速访问中序后继(如果节点的右指针是线索,则指向其后继),我们可以通过跟随其右指针来获取节点的后继,如果右指针是线索。否则,该节点的后继是其右子树中最左边的节点。
@staticmethod
def get_successor(node: Node) -> Optional[Node]:
if node.is_thread:
return node.right
else:
if node.right:
return RightThreadedBinaryTree.get_leftmost(node=node.right)
# if node.right is None, it means no successor of the given node.
return None
`get_predecessor` 的实现与二叉搜索树的前驱函数完全相同。
@staticmethod
def get_predecessor(node: Node) -> Optional[Node]:
if node.left:
return RightThreadedBinaryTree.get_rightmost(node=node.left)
parent = node.parent
while parent and node == parent.left:
node = parent
parent = parent.parent
return parent
中序遍历
右单线索二叉树提供的一个好处是,我们无需辅助栈或递归即可进行中序遍历。算法如下:
- 从整个树的最左边节点开始。
- 如果右指针是线索,则跟随右指针;如果右指针不是线索,则转到子树的最左边节点。
- 重复步骤 2,直到右指针为空。
下图中的红色箭头演示了带有线索的中序遍历。

并且实现该函数时无需使用辅助栈或递归。
def inorder_traverse(self) -> traversal.Pairs:
if self.root:
current: Optional[Node] = self.get_leftmost(node=self.root)
while current:
yield (current.key, current.data)
if current.is_thread:
current = current.right
else:
if current.right is None:
break
current = self.get_leftmost(current.right)
前序遍历
右单线索二叉树还提供了一种更简单的前序遍历方式,比中序遍历更简单。
- 从根节点开始。
- 如果左指针不为空,则转到左子节点。
- 如果左指针为空,则跟随线索转向右边。
- 重复步骤 2 和 3,直到右指针为空。
下图中的红色箭头显示了线索化前序遍历的路径。

前序遍历可以实现如下:
def preorder_traverse(self) -> traversal.Pairs:
current = self.root
while current:
yield (current.key, current.data)
if current.is_thread:
# If a node is thread, it must have a right child.
current = current.right.right # type: ignore
else:
current = current.left
左单线索二叉搜索树
左单线索二叉树与右单线索二叉树是对称的。在左单线索二叉树中,如果任何节点的左指针为空,则该左指针是线索,指向该节点的中序前驱,并且 `is_thread` 变量设置为 `True`。左单线索二叉树的形象化如下图所示。

左单线索二叉树的类结构与右单线索二叉树几乎相同。唯一的区别是,左单线索二叉树提供简单的反中序遍历,而不是中序和前序遍历。
class LeftThreadedBinaryTree:
def __init__(self) -> None:
self.root: Optional[Node] = None
def __repr__(self) -> str:
"""Provie the tree representation to visualize its layout."""
if self.root:
return (
f"{type(self)}, root={self.root}, "
f"tree_height={str(self.get_height(self.root))}"
)
return "empty tree"
def search(self, key: Any) -> Optional[Node]:
…
def insert(self, key: Any, data: Any) -> None:
…
def delete(self, key: Any) -> None:
…
@staticmethod
def get_leftmost(node: Node) -> Node:
…
@staticmethod
def get_rightmost(node: Node) -> Node:
…
@staticmethod
def get_successor(node: Node) -> Optional[Node]:
…
@staticmethod
def get_predecessor(node: Node) -> Optional[Node]:
…
@staticmethod
def get_height(node: Optional[Node]) -> int:
…
def reverse_inorder_traverse(self) -> traversal.Pairs:
…
Insert
`insert` 操作类似于右单线索二叉树。区别在于线索在左侧。
- 通过从根节点开始遍历树,并将新节点键与沿途每个节点的键进行比较,找到插入新节点的合适位置(即新节点的父节点)。向左子树遍历时,还要检查 `is_thread` 变量。如果该变量为 `True`,则表示我们已到达叶子节点,该叶子节点就是父节点。
- 找到父节点后,更新父节点的左指针(或右指针,取决于键值)指向新节点。
- 更新新节点的 parent 属性以指向父节点。
- 如果新节点是父节点的右子节点,则将新节点的左指针指向父节点,并将 `is_thread` 变量设置为 `True`。
- 如果新节点是父节点的左子节点,则将父节点的左指针(在插入之前,父节点的左指针必须是线索)复制到新节点的左指针,并将 `is_thread` 设置为 `True`。更新父节点的左指针指向新节点。
下图演示了节点插入的步骤。

实现如下:
def insert(self, key: Any, data: Any) -> None:
new_node = Node(key=key, data=data)
parent: Optional[Node] = None
current: Optional[Node] = self.root
while current:
parent = current
if new_node.key < current.key:
# If the node is thread, meaning it's a leaf node.
if current.is_thread:
current = None
else:
current = current.left
elif new_node.key > current.key:
current = current.right
else:
raise tree_exceptions.DuplicateKeyError(key=new_node.key)
new_node.parent = parent
# If the tree is empty
if parent is None:
self.root = new_node
elif new_node.key > parent.key:
parent.right = new_node
# Update thread
new_node.left = parent
new_node.is_thread = True
else:
# Update thread
new_node.is_thread = parent.is_thread
new_node.left = parent.left
parent.is_thread = False
# Parent's left must be set after thread update
parent.left = new_node
搜索
搜索操作与右单线索二叉树类似,因此我们需要检查 `is_thread` 变量来确定我们是否到达了叶子节点。
- 从根节点开始遍历树,并将要查找的键与沿途每个节点的键进行比较。
- 如果键匹配,则找到了该节点。
- 如果在到达叶子节点后(如果 `is_thread` 为 `True`,也表示该节点是叶子节点)仍未找到匹配的键,则表示该键不存在于树中。
实现与右单线索二叉树的搜索非常相似。
def search(self, key: Any) -> Optional[Node]:
current = self.root
while current:
if key == current.key:
return current
elif key < current.key:
if current.is_thread is False:
current = current.left
else:
break
else: # key > current.key:
current = current.right
return None
删除
同样,左单线索二叉树的删除与右单线索二叉树是对称的,也分为三种情况:无子节点、只有一个子节点、有两个子节点。
情况 1:无子节点

情况 2a:只有一个左子节点

情况 2b:只有一个右子节点

情况 3:有两个子节点
3.a 要删除节点的右子节点也是右子树中最左边的节点。

3.b 要删除节点的右子节点也有两个子节点。
被替换节点没有子节点

被替换节点只有一个右子节点:

与右单线索二叉树一样,我们也使用在二叉搜索树删除中使用的替换(transplant)技术来用要删除的节点替换子树。
def delete(self, key: Any) -> None:
if self.root and (deleting_node := self.search(key=key)):
# Case 1: no child
if deleting_node.right is None and (
deleting_node.left is None or deleting_node.is_thread
):
self._transplant(deleting_node=deleting_node, replacing_node=None)
# Case 2a: only one left child
elif (deleting_node.right is None) and (deleting_node.is_thread is False):
self._transplant(
deleting_node=deleting_node, replacing_node=deleting_node.left
)
# Case 2b: only one right child
elif deleting_node.right and (
deleting_node.is_thread or deleting_node.left is None
# deleting_node.left is None means the deleting node is the root.
):
successor = self.get_successor(node=deleting_node)
if successor:
successor.left = deleting_node.left
self._transplant(
deleting_node=deleting_node, replacing_node=deleting_node.right
)
# Case 3: two children
elif deleting_node.right and deleting_node.left:
replacing_node: Node = self.get_leftmost(node=deleting_node.right)
successor = self.get_successor(node=replacing_node)
# the leftmost node is not the direct child of the deleting node
if replacing_node.parent != deleting_node:
self._transplant(
deleting_node=replacing_node,
replacing_node=replacing_node.right,
)
replacing_node.right = deleting_node.right
replacing_node.right.parent = replacing_node
self._transplant(
deleting_node=deleting_node, replacing_node=replacing_node
)
replacing_node.left = deleting_node.left
replacing_node.left.parent = replacing_node
replacing_node.is_thread = False
if successor and successor.is_thread:
successor.left = replacing_node
else:
raise RuntimeError("Invalid case. Should never happened")
def _transplant(self, deleting_node: Node, replacing_node: Optional[Node]) -> None:
if deleting_node.parent is None:
self.root = replacing_node
if self.root:
self.root.is_thread = False
elif deleting_node == deleting_node.parent.left:
deleting_node.parent.left = replacing_node
if replacing_node:
if deleting_node.is_thread:
if replacing_node.is_thread:
replacing_node.left = deleting_node.left
else:
deleting_node.parent.left = deleting_node.left
deleting_node.parent.is_thread = True
else: # deleting_node == deleting_node.parent.right
deleting_node.parent.right = replacing_node
if replacing_node:
if deleting_node.is_thread:
if replacing_node.is_thread:
replacing_node.left = deleting_node.left
if replacing_node:
replacing_node.parent = deleting_node.parent
获取高度
`get_height` 函数与右单线索二叉树的实现是对称的。
@staticmethod
def get_height(node: Optional[Node]) -> int:
if node:
if node.right and node.is_thread is False:
return (
max(
LeftThreadedBinaryTree.get_height(node.left),
LeftThreadedBinaryTree.get_height(node.right),
)
+ 1
)
if node.right:
return LeftThreadedBinaryTree.get_height(node=node.right) + 1
if node.is_thread is False:
return LeftThreadedBinaryTree.get_height(node=node.left) + 1
return 0
获取最左侧和最右侧节点
由于左单线索二叉树与右单线索二叉树是对称的,因此在尝试获取最左节点时,我们需要检查 `is_thread` 是否为 `True` 并检查左指针是否为空。
@staticmethod
def get_leftmost(node: Node) -> Node:
current_node = node
while current_node.left and current_node.is_thread is False:
current_node = current_node.left
return current_node
`get_rightmost` 的实现与二叉搜索树中的 `get_rightmost` 完全相同。
@staticmethod
def get_rightmost(node: Node) -> Node:
current_node = node
while current_node.right:
current_node = current_node.right
return current_node
前驱和后继
根据左单线索二叉树的定义:节点的空左指针指向其中序前驱。我们可以通过跟随线索来获取节点的“前驱”,如果节点的 `is_thread` 为 `True`。
@staticmethod
def get_predecessor(node: Node) -> Optional[Node]:
if node.is_thread:
return node.left
else:
if node.left:
return LeftThreadedBinaryTree.get_rightmost(node=node.left)
# if node.left is None, it means no predecessor of the given node.
return None
`get_successor` 的实现与二叉搜索树的后继函数完全相同。
@staticmethod
def get_successor(node: Node) -> Optional[Node]:
if node.right:
return LeftThreadedBinaryTree.get_leftmost(node=node.right)
parent = node.parent
while parent and node == parent.right:
node = parent
parent = parent.parent
return parent
反中序遍历
通过左线索,左单线索二叉树在执行反中序遍历时既不需要递归也不需要辅助栈。
- 从整个树的最右边节点开始。
- 如果左指针是线索,则跟随线索;如果左指针不是线索,则转到子树的最右边节点。
- 重复步骤 2,直到左指针为空。
下图中的红色箭头演示了带有线索的反中序遍历。

以下是实现:
def reverse_inorder_traverse(self) -> traversal.Pairs:
if self.root:
current: Optional[Node] = self.get_rightmost(node=self.root)
while current:
yield (current.key, current.data)
if current.is_thread:
current = current.left
else:
if current.left is None:
break
current = self.get_rightmost(current.left)
测试
一如既往,我们应该尽可能为我们的代码编写单元测试。在这里,我们使用在“Python 系列:构建二叉搜索树”中创建的 `conftest.py` 文件中的 `basic_tree` 函数来测试我们的单线索二叉树。完整的单元测试请参见 test_single_threaded_binary_trees.py。
分析
线索二叉树操作的运行时间与普通二叉搜索树的操作相同。

尽管右单线索二叉树提供了更简便的方式来获取节点的后继,左单线索二叉树提供了更直接的方式来获取节点的前驱,但线索并未在运行时间上节省太多。主要原因是这些函数仍然需要调用 `get_leftmost` 和 `get_rightmost` 函数,它们的平均运行时间为 O(lg n),最坏情况下的运行时间为 O(n)。
然而,线索确实在特定遍历方式上节省了空间复杂度。

示例
为二叉搜索树添加线索会使其实现更加复杂,但当遍历是关键需求,同时又需要考虑空间消耗时,它们可以提供一种解决方案。例如,我们想构建一个数据库,用户需要频繁地按升序和降序访问数据,但我们内存有限(即由于空间消耗考虑,无法使用辅助栈或递归)。在这种情况下,我们可以使用线索二叉树来实现用于升序和降序访问的索引。
from typing import Any
from forest.binary_trees import single_threaded_binary_trees
from forest.binary_trees import traversal
class MyDatabase:
"""Example using threaded binary trees to build an index."""
def __init__(self) -> None:
self._left_bst = single_threaded_binary_trees.LeftThreadedBinaryTree()
self._right_bst = single_threaded_binary_trees.RightThreadedBinaryTree()
def _persist(self, payload: Any) -> str:
"""Fake function pretent storing data to file system.
Returns
-------
str
Path to the payload.
"""
return f"path_to_{payload}"
def insert_data(self, key: Any, payload: Any) -> None:
"""Insert data.
Parameters
----------
key: Any
Unique key for the payload
payload: Any
Any data
"""
path = self._persist(payload=payload)
self._left_bst.insert(key=key, data=path)
self._right_bst.insert(key=key, data=path)
def dump(self, ascending: bool = True) -> traversal.Pairs:
"""Dump the data.
Parameters
----------
ascending: bool
The order of data.
Yields
------
Pairs
The next (key, data) pair.
"""
if ascending:
return self._right_bst.inorder_traverse()
else:
return self._left_bst.reverse_inorder_traverse()
if __name__ == "__main__":
# Initialize the database.
my_database = MyDatabase()
# Add some items.
my_database.insert_data("Adam", "adam_data")
my_database.insert_data("Bob", "bob_data")
my_database.insert_data("Peter", "peter_data")
my_database.insert_data("David", "david_data")
# Dump the items in ascending order.
print("Ascending...")
for contact in my_database.dump():
print(contact)
print("\nDescending...")
# Dump the data in decending order.
for contact in my_database.dump(ascending=False):
print(contact)
(完整示例可在 single_tbst_database.py 中找到。)
输出将如下所示:
Ascending...
('Adam', 'path_to_adam_data')
('Bob', 'path_to_bob_data')
('David', 'path_to_david_data')
('Peter', 'path_to_peter_data')
Descending...
('Peter', 'path_to_peter_data')
('David', 'path_to_david_data')
('Bob', 'path_to_bob_data')
('Adam', 'path_to_adam_data')
摘要
尽管添加线索会增加复杂性且不会提高运行时间性能,但线索二叉树利用了左指针或右指针的空闲空间,并提供了一种简单的方式来检索前驱或后继,以及一种无需使用栈或递归即可执行某些遍历的解决方案。当考虑空间复杂度且特定遍历(例如中序遍历)至关重要时,线索二叉树可以成为一种选择。
下一篇文章将构建双线索二叉树,它将结合单线索二叉树的优点,但也会更加复杂。
历史
- 2021年4月3日:初始版本
