二维插值函数
5.00/5 (23投票s)
各种二维插值算法
引言
二维插值在图像处理和数字地形建模等许多应用中都有体现。在这里,我们将比较不同的插值策略。
插值的目的是通过创建中间点来“密集化”稀疏数据集。在我们的示例中,我们将使用一个 4x5 的矩阵,并为每个值分配一个任意颜色。我们将原始数据集中的每个区间划分为 N=100 个点,从而创建一张 300x400 像素的图像。
这是我们的初始矩阵

方法 1 - 简单方法 - 最近邻插值
最简单的插值策略就是取最近数据点的值。它也可以称为“零阶插值”,由函数定义:nni(x,y)=Vround(x),round(y)。输出矩阵通过 M[i,j]=nni(i/N, j/N) 生成。
这是结果矩阵的颜色图

下面是穿过原始数据集第二行的截面图。它显示了初始数据点和插值后的值

观察截面图,注意那些导致颜色突然变化的突然跳跃。
虽然这种方法看起来几乎过于简单,但如果原始数据集足够密集且数据点不太嘈杂,这种方法可以获得可接受的结果。
方法 2 - 流行方法 - 双线性插值
这是最流行的方法之一。插值函数在 X 和 Y 方向上都是线性的(因此得名 - 双线性)

其中 frac(x) 是 x 的小数部分。结果矩阵是 M[i,j]=blin(i/N,j/N)。颜色图表示如下

这是截面图

现在,观察截面图,您可以看到没有突然的跳跃(插值函数是连续的)。但是,斜率有突然的变化(用微积分的术语来说,一阶导数不连续),这会在颜色图中产生菱形伪影。
方法 3 - 错误方法 - 双二次插值
如果一阶(线性)函数得到了连续的插值函数,但导数不连续,那么二阶(称为二次或抛物线)函数是否会得到更好的插值函数?
我在 NGS GEOCON 程序中遇到过这种方法,我能找到的最早的版本是在 GEOID90 插值程序中。
该方法不使用线性函数,而是使用二阶函数
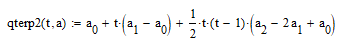
其中 t 的范围是 0 到 2。可以看出 qterp2(0)=a0, qterp2(1)=a1 和 qterp2(2)=a2。
这些条件唯一地确定了二阶函数的系数,因此我们无法强制使一阶导数连续。
一维插值通过先沿 X 轴进行 3 次插值(Y 值递增),然后沿 Y 轴对产生的 3 个值进行插值,来扩展到二维。结果的颜色图是

截面图是

为了更好地理解发生了什么,让我们检查一下一维插值。我们有 3 个函数:q1 通过前 3 个点,q2 通过点 2、3、4,q3 通过点 3、4、5。然后我们有将每个函数的片段组合起来的插值函数

下面的图显示了插值函数是如何组合的

一阶导数的不连续性比线性插值的情况更明显。从线性函数变为抛物线函数并没有带来任何明显的优势。我们仍然会有斜率的急剧变化,结果曲面看起来比双线性插值更奇怪。增加的复杂性并没有带来任何好处。
方法 4 - 复杂方法 - 双三次插值
如果我们想要斜率连续,我们需要提高一个阶数到三次函数。双三次函数可以表示为

或用矩阵表示

挑战在于找到 16 个系数的值。它们可以通过求解由以下公式组成的方程组来确定:
- 插值正方形每个角的函数值有 4 个方程
- 插值正方形每个角的偏导数有 8 个方程(X 方向 4 个,Y 方向 4 个)
- 插值正方形每个角的混合导数有 4 个方程
偏导数或混合导数的值通过相邻数据点之间的差值来估计。
现在,为每个插值正方形求解 16 个方程组成的方程组并不是实现高效算法的最佳方法。幸运的是,事实证明 如果我们写出 16 个方程,这个方程组可以写成

其中 V 是数据点的值,Vx 是 X 方向的偏导数,Vy 是 Y 方向的偏导数,Vxy 是交叉导数。W 矩阵是一个固定的矩阵,不依赖于数据点。系数 a 的值可以从

找到。W 的逆矩阵可以预先计算,求解方程组就简化为“仅仅”一次矩阵乘法。供参考,这是 W 矩阵的逆

您也可以在维基百科的 双三次插值 页面上找到它。
我们数据集的结果颜色图是

以及截面图

插值函数确实是连续的,斜率也是连续的,但它可能有过冲和欠冲。它们源于我们对偏导数的相当任意的估计——请记住,它们被假定为相邻数据点之间的差值。无论如何,如果您决定使用双三次插值,这些过冲是不可避免的,您必须考虑到它们并相应地进行缩放或截断。
方法 5 - 我的方法 - 受约束的双三次插值
可以通过强制每个数据点的偏导数和交叉导数等于 0 来修改双三次算法。
这简化了双三次系数的求解过程,并将它们简单地变成了一个权重函数

插值函数变成

结果矩阵是 M[i,j]=cbi(i/N,j/N)。颜色图表示如下

截面图

显示插值函数是连续的,并且斜率也是连续的。此外,在每个数据点处斜率为 0,这可以防止任何过冲或欠冲。
如果我们回顾双线性插值方法,插值公式可以重写为
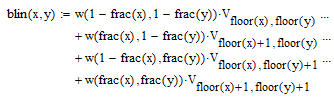
但使用权重函数

这意味着我们只需更改权重函数,就可以在受约束的双三次插值和双线性插值之间切换。
历史注释:我多年前在一个建议 GPS 接收器如何从(非常稀疏的)大地水准面模型中内插 MSL 高度(平均海平面高度)的文档中发现了这个算法。不幸的是,我不记得确切的出处,也找不到任何参考。
展示代码
文件 interp2.h 包含了上述所有算法
// Nearest neighbor interpolation
template<typename T>
void nni (const Matrix<T>& in, Matrix<T>& out)
// Bilinear interpolation
template<typename T>
void bilin (const Matrix<T>& in, Matrix<T>& out)
// Biquadratic interpolation
template<typename T>
void biquad (const Matrix<T>& in, Matrix<T>& out)
// Bicubic interpolation
template<typename T>
void bicube (const Matrix<T>& in, Matrix<T>& out)
// Constrained bicubic interpolation
template<typename T>
void cbi (const Matrix<T>& in, Matrix<T>& out)
它们都需要某种矩阵来表示数据。我强烈建议在进行任何严肃的工作时使用专业的矩阵代数包。除非您是喜欢重新发明轮子的天才,否则不要自己编写。我个人偏爱 Eigen,但也有很多选择。
话虽如此,interp2.h 文件包含了一个非常简单的 Matrix 类实现。它包含了插值算法所需的绝对最少的操作。您可以将其用于熟悉插值方法,或者在无法使用更好的矩阵包时使用。
结论
我已经介绍了最常见的二维插值方法。选择哪种方法取决于具体情况,但不用说,我的最爱是方法 5。
历史
- 2021 年 9 月 13 日 - 初始版本
