FORTRAN 信号处理音频 C

可定制的 Butterworth 数字滤波器

Andy Allinger

4.94/5 (9投票s)

2021年9月19日

公共领域

6分钟阅读

15360

426

由通带频率、阻带频率、通带衰减和阻带衰减指定的滤波器

下载 bfilt0.zip - 8.3 KB

引言

实现数字滤波器所需的大部分信息都包含在 Robert Bristow-Johnson 撰写的广为人知的网络文本《音频双二阶滤波器系数的食谱公式》[2001?] 中。不幸的是，该文档并未解释一些重要的细节。公式以截止频率 f₀ 的形式给出。这是能量衰减一半的频率，既不是要保留的频率，也不是要消除的频率，而是介于两者之间的过渡带中的某个频率。食谱公式还要求指定品质因数 Q，但并未解释如何选择 Q。

本文将回答这两个未知的问题。将根据 [Stensby, 2005] 的设计指南开发一个 Butterworth 低通滤波器。稍作简单的修改即可得到高通滤波器。同时使用低通滤波器和高通滤波器可以得到带通滤波器。子程序 bfilt 根据请求的通带频率是否小于或大于请求的阻带频率，充当低通滤波器或高通滤波器。

背景

(有关 Butterworth 滤波器的理论处理，请参阅 codeproject 文章 “C# 中的低通、高通和带通 Butterworth 滤波器”)

数字信号是在等间隔时间测量的幅度序列。通常，这代表声音，但也可以是任何东西：雷达系统测量的电压或脑电波。

数字滤波器通过移除选定的频率并保持其他频率不变来修改信号。滤波器在时域工作，因此无需对信号进行傅里叶变换。

过渡带

在降低信号的采样率之前，重要的是要通过低通滤波器将其运行，以移除大于新采样率一半的频率。假设您想将某些音频的采样率从每秒 44,100 个样本降低到每秒 4,410 个样本。那么新的最大频率将是该值的一半，即每秒 2,205 个周期。理想情况下，您希望保留 2,205 Hz 以下的所有内容并拒绝其上方的内容。这并非完全可以实现。代替在保留和拒绝之间具有完全锐利的过渡，存在一个过渡带。这是能量从通带逐渐衰减到阻带的频率范围。

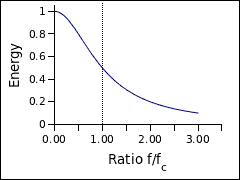
上图显示，在截止频率 (f/fc = 1) 处，一半能量通过滤波器。

滤波器种类

有几种数字滤波器，包括 Butterworth、Elliptical 和 Chebyshev。 Butterworth 滤波器是一个受欢迎的选择，因为它在通带内的衰减很小，但代价是过渡带很宽。 Butterworth 滤波器有不同的阶数。通过增加阶数可以使过渡带变窄。

方程

鉴于

f_p: 通带边缘的频率
f_s: 阻带边缘的频率
H_p: 通带内的最小传输
H_s: 阻带内的最大传输

查找

f_c: 截止频率
n: 滤波器的阶数

对于低通滤波器，根据 [Stensby, 2005]，

$\epsilon = \sqrt{(\frac{1}{H_p})^2 - 1}$

$D = \frac{1}{H_s}$

$n = \frac{\log(\frac{\epsilon}{\sqrt{D^2-1}})}{\log(\frac{f_p}{f_s})}$

选择截止频率以满足阻带规范，并可能超出通带规范

$f_c = f_s \sqrt{D^2 - 1}^{\frac{-1}{n}}$

对于高通滤波器，进行简单的修改

$n = \frac{\log(\frac{\epsilon}{\sqrt{D^2-1}})}{\log(\frac{f_s}{f_p})}$

$f_c = f_s \sqrt{D^2 - 1}^{\frac{+1}{n}}$

接下来是选择 Q 的问题。根据 [David S. 2010]

引用

[Butterworth 滤波器的维基百科页面] 中间部分是“多项式的因子...” 表。 4 位或 5 位数字是 1/Q，因此它们的倒数就是您要查找的数字... 一般来说，任何更高阶的滤波器形状都可以分成一系列二阶部分 + 一个一阶部分（如果需要奇数阶）。每个部分都有自己的 Q，更高阶的滤波器将具有从低 Q 到高 Q 的递进。

Wiki 提供了这些数字的公式。将有 $\frac{N}{2}$ 次通过滤波器，以及一系列 $\frac{N}{2}$ 个值。因此所需的方程是

$Q = \frac{-\frac{1}{2}}{\cos(\pi \frac{2 k + n - 1}{2 n})}$

其中 $k = \frac{N}{2} ... 1$

现在可以进行食谱公式了。主要变换方程是

$y_i = a_0 x_i + a_1 x_{i-1} + a_2 x_{i-2} - b_1 y_{i-1} - b_2 y_{i-2}$

查找中间变量

$\omega_0 = \frac{2 \pi f_c}{f_s}$ $R = \frac{\sin(\omega_0)}{2 Q}$

低通滤波器的系数是

$a_0 = \frac{1 - \cos(\omega_0)}{2 (1 + R)}$ $a_1 = \frac{1 - \cos(\omega_0)}{1 + R}$ $a_2 = a_0$ $b_1 = \frac{-2 \cos(\omega_0)}{1 + R}$ $b_2 = \frac{1 - R}{1 + R}$

高通滤波器的系数是

$a_0 = \frac{1 + \cos(\omega_0)}{2 (1 + R)}$ $a_1 = \frac{-(1 + \cos(\omega_0))}{1 + R}$ $a_2 = a_0$ $b_1 = \frac{-2 \cos(\omega_0)}{1 + R}$ $b_2 = \frac{1 - R}{1 + R}$

使用代码

bfilt 的原型是

int bfilt (double *s, int l, double fsamp, 
double fpass, double fstop, double hpass, double hstop);

s 是一个包含样本数据的数组
l 是数组的长度
fsamp 是每秒的采样率
fpass 是通带边缘的频率（以周期/秒为单位）
fstop 是阻带边缘的频率（以周期/秒为单位）
hpass 是通带内的最小传输分数，例如 0.99
hstop 是阻带内的最大传输分数，例如 0.01
返回值为零表示没有错误。

示例问题

测试程序 t_filt 读取名为 input.raw 的音频文件。为简单起见，音频文件必须是单声道、16 位整数样本、小端字节序，无头信息。以下是 TheScarlettWitch89 [2019] 录制的一些简短歌唱。由于空间限制，如果您想听结果，您需要从 freesound 下载此文件并自行转换。在 audacity 中加载输入文件，它会生成频谱图：