65.9K
CodeProject 正在变化。 阅读更多。
Home

四旋翼飞行器的最优控制

Igor Ladnik
starIconstarIconstarIconstarIconstarIcon

5.00/5 (27投票s)

2022年6月20日

CPOL

20分钟阅读

viewsIcon

11745

downloadIcon

488

为四旋翼飞行器的基本飞行模式自动生成最优控制策略

目录

简介

无人机（UAVs）通常指多旋翼直升机，具有广泛的应用。它们可以作为技术机器人、各种设备（如传感器、摄像头、机械臂、武器等）的平台。它们也成为战场、执法和生命救援任务中的重要因素（例如，以色列军队的这项惊人的“母无人机”任务，拯救了一只罕见的秃鹫幼崽）。因此，近年来，大量工作致力于无人机的设计和控制也就不足为奇了。我对此也感兴趣，纯粹是出于爱好。我选择四轴飞行器作为受控对象。

维基百科：四旋翼或四轴飞行器是一种有四个旋翼的直升机。

本文介绍了我的迭代线性二次调节器（ILQR）版本（在我另一篇 CodeProject 文章简单最优控制软件中简要描述，下文简称 [1]）在四轴飞行器控制中的应用。动机是采用统一的方法来优化四轴飞行器的不同机动。现代移动设备（安装在四轴飞行器上）的计算能力允许执行复杂的计算。实施 ILQR 所需的计算，尽管相当复杂，但在适当的代码优化后可能可以自主执行。这种方法可以用于飞行器的自动驾驶仪。目标是计算状态向量的反馈，并计算不同飞行模式下闭环系统的独立输入。

带摄像头的飞行四轴飞行器（图片来自此处）。

四轴飞行器（图片来自此处）。

四轴飞行器动态模型

从动态角度看，四轴飞行器构成一个复杂的非线性系统。四轴飞行器的动态模型在许多著作中都有描述。因此，我们在此不作讨论。由于我的目标是原则上展示 [1] 中控制策略生成算法在四轴飞行器动力学中的适用性，因此采用了简化的动态模型。所有空气阻力、螺旋桨引起的湍流等影响均被忽略。电机驱动的动力学也未考虑。该模型的数学描述主要来自此处。即使有上述假设，动态模型的状态向量 x 的维度为 12，输入控制向量 m 的维度为 4。

Quadcopter structure and frames configuration

四轴飞行器结构和框架配置。

符号列表

名称 描述 单位
x、y、z 相对于惯性系的姿态 m
xB、yB、zB 机体系轴  
xE、yE、zE 惯性系轴  
φ、θ、ψ 欧拉角（横滚、俯仰、偏航） 弧度、度
ωi 转子 i 的角速度 弧度/秒
M 四轴飞行器质量 千克
Jx、Jy、Jz 转动惯量 kg · m2
l 力臂 m
T 总推力 N
τφ、τθ、τψ 对质心的扭矩 m · s
b 转子阻力系数  
d 转子推力系数  

独立输入（开环控制输入 - 向量 m）的数学描述

T = b ⋅ (ω12 + ω22 + ω32 + ω42) = m1
τφ = b ⋅ l ⋅ (ω42 - ω22) = m2
τθ = b ⋅ l ⋅ (ω32 - ω12) = m3
τψ = d ⋅ (ω22 + ω42 - ω12 - ω32) = m4

从以上公式可以看出，输入 mi 唯一地取决于旋翼的角速度 ωi，而 ωi 又由为旋翼供电的电机的电压控制。这四个电机的电压是实际受控的独立输入。为简单起见，这里我们假设电机电压与输入 mi 之间存在直接的非惯性依赖关系。这使得我们可以将输入 mi，即向量 m，视为开环系统的独立输入。

状态向量 x 的数学描述

x1 = φ ẋ1 = x2
x2 = dφ/dt      ẋ2 = a1 ⋅ x4 ⋅ x6 + b1 ⋅ m2
x3 = θ ẋ3 = x4
x4 = dθ/dt ẋ4 = a2 ⋅ x2 ⋅ x6 + b2 ⋅ m3
x5 = ψ ẋ5 = x6
x6 = dψ/dt ẋ6 = a3 ⋅ x2 ⋅ x4 + b3 ⋅ m4
x7 = x ẋ7 = x8 (1)
x8 = dx/dt ẋ8 = (cosx1 ⋅ sinx3 ⋅ cosx5 + sinx1 ⋅ sinx5) ⋅ m1 / M
x9 = 是 ẋ9 = x10
x10 = dy/dt ẋ10 = (cosx1 ⋅ sinx3 ⋅ sinx5 - sinx1 ⋅ cosx5) ⋅ m1 / M
x11 = z ẋ11 = x12
x12 = dz/dt ẋ12 = (cosx1 ⋅ cosx3) ⋅ m1 / M - g

 

a1 = (Jy - Jz) / Jx
a2 = (Jz - Jx) / Jy
a3 = (Jx - Jy) / Jz
b1 = l / Jx
b2 = l / Jy
b3 = l / Jz

表数值

参数 值 单位
g 9.81 米/秒2
M 0.65 千克
l 0.23 m
Jx 7.5 · 10-3 kg · m2
Jy 7.5 · 10-3 kg · m2
Jz 1.3 · 10-2 kg · m2

方法

这项工作的数学原理在 [1] 中以非常简化的方式进行了描述。下面我将引用 [1] 中的图片、符号和公式。下文符号 [1](x) 表示 文章 [1] 中的公式 x。

上述四轴飞行器动态模型被视为一个需要优化的开环系统，即最小化成本函数 [1](2)。

开环控制系统

解决方案将以闭环系统形式获得

闭环控制系统

参数如 [1](7) 所示

mk = cN-k - LN-k ⋅ xk

其中
LN-k 通常是与时间相关的，来自状态向量 x 坐标的反馈矩阵，
cN-k 是闭环系统的输入向量，
N 是总时间步数，以及
k 是当前时间步数，k = 0, 1, ..., N - 1。

四轴飞行器的动态系统是高度非线性的（尤其是在欧拉角较大时）。因此，我们使用迭代方法来生成 L 和 c。为了实现迭代优化，我们不仅需要微分方程 [1](1)，对应于上述动态系统的 (1) 式，还需要偏导数 [1](9)。后者可以通过分析或数值方法获得（[1] 提供了这两种方法的示例）。在这里，我们使用偏导数的解析表示，在代码中称为 梯度。

优化过程结束后，我们对计算出的反馈矩阵 LN-k 进行非常基本的分析。计算矩阵所有分量的平均值。这个“平均”矩阵可以为理解控制算法提供线索。特别是，它展示了状态向量坐标对输入的影响。在某些情况下，少数坐标仅通过其反馈影响一个输入。这使我们能够假设这些坐标由一个单独的输入控制。在这种情况下，具有多个输入的一般控制系统可以分解为几个独立的单输入子系统。

代码

代码以纯 C# 编写，使用 .NET 6.0 和 .NET Standard 2.0，因此可以在 Windows、Linux 和 macOS 下运行。代码与 [1] 中的软件没有本质区别。委托 CalcDelegate 稍微简化，只有两个参数

public delegate double CalcDelegate(Vector m, Vector x);

方法 FeedbackAnalysis() 已添加到 IBase 接口并在 Base 类中实现，用于执行反馈矩阵“平均”。结果写入到输出目录中名为 {caseId}_AverageFeedback.txt 的文本文件。一个显著的增强是 Plot 项目，用于即时生成瞬态图。它使用 Python 代码，因此应该安装 Python3 才能使用此新功能。不同的优化和模拟案例可以并行运行。

文件 Program.cs 包含动态系统的创建和处理调用。Linear、VanDerPol 和 Rayleigh 案例是从 [1] 中采用的，并更新了代码用于测试目的，默认情况下已注释掉。这里的重点是 Quad。其 Process() 方法以及函数和梯度的计算如下所示

    public INonLinearQ[] Process()
    {
        const string Title = "Quadcopter";
        Console.WriteLine($"Begin \"{Title}\"");

        var outputFormat = GetOutputFormatting();
        var data = DataTransformation(GetConfig<QuadData>());
        (g, mass, a, b) = GetModelParameters(data);

        ConcurrentBag<INonLinearQ> cbagDynamicSystem = new();

        Parallel.ForEach(data.ControlCases, c =>
        {
            #region Iterations Settings

            Vector desirableX = new(c.desirableX);
            var Q = new Matrix(dimensionX, dimensionX).MakeDiag(c.diagQ);
            Vector desirableU = new(c.desirableU);
            var Z = new Matrix(dimensionU, dimensionU).MakeDiag(c.diagZ);
            Vector xInit = new(c.xInit);

            #endregion // Iterations Settings

            #region Optimization

            const string Act = "Optimization";

            // Exact formulas for gradients computing
            cbagDynamicSystem.Add(
                (SQ.Create(Functions, GradientsA, GradientsB, Q, Z,
                           desirableX, desirableU, c.dt, xInit, c.N)
                   .Config(c)
                   .RunOptimization()
                   .Output2Csv(Act, outputFormat)
                   .Plots(DrawPlots, Act) as INonLinearQ)
                   .OutputExecutionDetails(isExactGradient: true)
            );

            #endregion // Optimization
        });

        // Simulation
        cbagDynamicSystem.Simulate(outputFormat, data.Simulations, DrawPlots);

        Console.WriteLine($"End \"{Title}\"{Environment.NewLine}{Environment.NewLine}");

        return cbagDynamicSystem.ToArray();
    }
    private CalcDelegate[] Functions =>
        new CalcDelegate[]
        {
            /* 1*/ (m, x) => x[_(2)],

            /* 2*/ (m, x) => a[_(1)] * x[_(4)] * x[_(6)] + b[_(1)] * m[_(2)],

            /* 3*/ (m, x) => x[_(4)],

            /* 4*/ (m, x) => a[_(2)] * x[_(2)] * x[_(6)] + b[_(2)] * m[_(3)],

            /* 5*/ (m, x) => x[_(6)],

            /* 6*/ (m, x) => a[_(3)] * x[_(2)] * x[_(4)] + b[_(3)] * m[_(4)],

            /* 7*/ (m, x) => x[_(8)],

            /* 8*/ (m, x) => m[_(1)] / mass * ( C(x[_(1)]) *
                                                S(x[_(3)]) *
                                                C(x[_(5)]) + S(x[_(1)]) *
                                                             S(x[_(5)]) ),

            /* 9*/ (m, x) => x[_(10)],

            /*10*/ (m, x) => m[_(1)] / mass * ( C(x[_(1)]) *
                                                S(x[_(3)]) *
                                                S(x[_(5)]) - S(x[_(1)]) *
                                                             C(x[_(5)]) ),

            /*11*/ (m, x) => x[_(12)],

            /*12*/ (m, x) => m[_(1)] / mass * C(x[_(1)]) * C(x[_(3)]) - g,
        };

    private CalcDelegate[,] GradientsA
    {
        get
        {
            // Exact formulas for gradients computing
            var gradients = InitGradients(dimensionX, dimensionX);

            gradients[_(1), _(2)] = (m, x) => 1;

            gradients[_(2), _(4)] = (m, x) => a[_(1)] * x[_(6)];
            gradients[_(2), _(6)] = (m, x) => a[_(1)] * x[_(4)];

            gradients[_(3), _(4)] = (m, x) => 1;

            gradients[_(4), _(2)] = (m, x) => a[_(2)] * x[_(6)];
            gradients[_(4), _(6)] = (m, x) => a[_(2)] * x[_(2)];

            gradients[_(5), _(6)] = (m, x) => 1;

            gradients[_(6), _(2)] = (m, x) => a[_(3)] * x[_(4)];
            gradients[_(6), _(4)] = (m, x) => a[_(3)] * x[_(2)];

            gradients[_(7), _(8)] = (m, x) => 1;

            gradients[_(8), _(1)] = (m, x) => m[_(1)] / mass *
                (-S(x[_(1)]) * S(x[_(3)]) * C(x[_(5)]) + C(x[_(1)]) * S(x[_(5)]));

            gradients[_(8), _(3)] = (m, x) => m[_(1)] / mass *
                C(x[_(1)]) * C(x[_(3)]) * C(x[_(5)]);

            gradients[_(8), _(5)] = (m, x) => m[_(1)] / mass *
                (-C(x[_(1)]) * S(x[_(3)]) * S(x[_(5)]) + S(x[_(1)]) * C(x[_(5)]));

            gradients[_(9), _(10)] = (m, x) => 1;

            gradients[_(10), _(1)] = (m, x) => m[_(1)] / mass *
                (-S(x[_(1)]) * S(x[_(3)]) * S(x[_(5)]) - C(x[_(1)]) * C(x[_(5)]));

            gradients[_(10), _(3)] = (m, x) => m[_(1)] / mass *
                C(x[_(1)]) * C(x[_(3)]) * S(x[_(5)]);

            gradients[_(10), _(5)] = (m, x) => m[_(1)] / mass *
                (C(x[_(1)]) * S(x[_(3)]) * C(x[_(5)]) + S(x[_(1)]) * S(x[_(5)]));

            gradients[_(11), _(12)] = (m, x) => 1;

            gradients[_(12), _(1)] = (m, x) => -m[_(1)] / mass * S(x[_(1)]) * C(x[_(3)]);
            gradients[_(12), _(3)] = (m, x) => -m[_(1)] / mass * C(x[_(1)]) * S(x[_(3)]);

            return gradients;
        }
    }

    private CalcDelegate[,] GradientsB
    {
        get
        {
            // Exact formulas for gradients computing
            var gradients = InitGradients(dimensionX, dimensionU);

            gradients[_(2), _(2)] = (m, x) => b[_(1)];
            gradients[_(4), _(3)] = (m, x) => b[_(2)];
            gradients[_(6), _(4)] = (m, x) => b[_(3)];

            gradients[_(8), _(1)] = (m, x) => 1 / mass *
                (C(x[_(1)]) * S(x[_(3)]) * C(x[_(5)]) + S(x[_(1)]) * S(x[_(5)]));

            gradients[_(10), _(1)] = (m, x) => 1 / mass *
                (C(x[_(1)]) * S(x[_(3)]) * S(x[_(5)]) - S(x[_(1)]) * C(x[_(5)]));

            gradients[_(12), _(1)] = (m, x) => 1 / mass * C(x[_(1)]) * C(x[_(3)]);

            return gradients;
        }
    }

成功构建后，Dynamics 可以通过以下方式运行

dotnet Dynamics.dll

或在 Windows 中作为 Dynamics.exe 运行。

输出目录的路径（绝对或相对）在 App.config 中通过参数 RootOutputDir 定义。输出目录包含用于优化和模拟的目录，具体取决于正在计算的内容。每个此类目录都有 Excel 兼容的 CSV 文件，其中包含瞬态值，以及带有相应瞬态图的图像文件。此输出在代码中定义（Quad 类中的 GetOutputFormatting() 方法以及其他动态系统的类似代码）。Optimization/{caseId}/Log 目录还包含每个控制案例的多个日志文件，其中包含每个步骤每次迭代的状态、开环和闭环控制向量以及反馈矩阵。日志的详细程度由可配置参数 logLevel 定义。

配置

软件通过 JSON 配置文件进行配置。除了四轴飞行器动态参数外，文件还包含两个用于 ControlCases（优化）和 Simulations 的参数数组。在单个配置文件中，可以省略 Simulations 数组。配置文件的示例如下。

{
	"g": 9.81,    // m * sq(s)
	"l": 0.23,    // m
	"m": 0.65,    // kg
	"Jx": 7.5e-3, // kg * sq(m)
	"Jy": 7.5e-3, // kg * sq(m)
	"Jz": 1.3e-2, // kg * sq(m)

	// Stabilization from non-zero initial conditions
	"ControlCases": [
		{
			"Id": "Stabilization_1-1",
			"isPlotRequired": true,
			"logLevel": "short",
			"dt": 0.1,
			"N": 61,
			"maxIterations": 2,
			"inDegrees": false,
			"desirableX": [  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ],
			"diagQ": [ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 ],
			"desirableU": [ 0, 0, 0, 0 ],
			"diagZ": [ 0, 0, 0, 0 ],
			"xInit": [ 0.3, 1, -0.4, 1, 0.2, 1, 0, 1, 0, 1, 0, -1 ]
		},
		{
			"Id": "Stabilization_1-2",
			"isPlotRequired": true,
			"logLevel": "short",
			"dt": 0.1,
			"N": 61,
			"maxIterations": 2,
			"inDegrees": false,
			"desirableX": [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ],
			"diagQ": [ 10, 1, 10, 1, 10, 1, 10, 1, 10, 1, 10, 1 ],
			"desirableU": [ 0, 0, 0, 0 ],
			"diagZ": [ 0, 0, 0, 0 ],
			"xInit": [ 0.3, 1, -0.4, 1, 0.2, 1, 0, 1, 0, 1, 0, -1 ]
		}
	],
	"Simulations": [
		{
			"caseId": "Stabilization_1-1",
			"titleSuffix": "_(1)",
			"isPlotRequired": true,
			"inDegrees": false,
			"xInit": [ 0.3, 1, -0.4, 1, 0.2, 1, 0, 1, 0, 1, 0, -1 ]
		}
	]
}

上述文件包含 ControlCases 和 Simulations 两个数组。下表解释了每个数组的配置参数。

表 控制案例配置

参数 可能的值 描述
ID 字符串 唯一的控制案例标识符
isPlotRequired true / false 此案例是否需要绘图
logLevel "full" / "short" / "none" 日志的详细程度
inDegrees true / false 角度单位为度 (true) 或弧度 (false)
dt 双精度 > 0 采样间隔
N 整数 > 0 总时间步数
maxIterations 整数 > 0 非线性情况下的优化迭代次数
desirableX 双精度数组，维度 12 状态向量的期望值（向量 r）
diagQ 双精度数组，维度 12 对角状态权重矩阵 Q 的值
desirableU 双精度数组，维度 4 开环系统输入向量的期望值（向量 u）
diagZ 双精度数组，维度 4 对角输入权重矩阵 Z 的值
xInit 双精度数组，维度 12 初始状态 xinit

表 模拟配置

参数 可能的值 描述
ID 字符串 唯一的模拟案例标识符
caseId 字符串 对应的控制案例标识符
isPlotRequired true / false 此案例是否需要绘图
inDegrees true / false 角度单位为度 (true) 或弧度 (false)
titleSuffix 字符串 瞬态图标题的后缀
xInit 双精度数组，维度 12 初始状态 xinit

标准 C# 配置文件 App.config 包含一个相应的案例配置 JSON 文件列表和一个 ConfigFileSelector 参数，用于选择当前执行的案例。文件 App.config 还定义了 RootOutputDir 作为输出文件的目录。如上所述，Python 代码用于即时生成瞬态图。Python.exe 的绝对路径可以通过环境变量 PYTHON 定义，或者如果未设置，则通过 App.config 文件中的参数 Python 定义。App.config 文件如下所示

<?xml version="1.0" encoding="utf-8" ?>
<configuration>
	<appSettings>
		<!-- ////////////////////////////////////////////////////////////// -->
		<!-- Location of the case configuration file (only one is expected) -->

		<!-- Case configuration file selector -->
		<add key="ConfigFileSelector" value="s1" />

		<!-- Case configuration file (relative to working directory) -->

		<!-- Stabilization -->
		<add key="s1" value="ControlCases\Stabilization\Stabilization_1.json" />
		<add key="s2" value="ControlCases\Stabilization\Stabilization_2.json" />

		<!-- Transition -->
		<add key="t1" value="ControlCases\Transition\Transition_1_(10, -1, 1).json" />
		<add key="t2" value="ControlCases\Transition\Transition_2_(100, 10, 20).json" />

		 <!-- Acceleration -->
		<add key="a1"
             value="ControlCases\Acceleration\Acceleration_1_XY_(2, -3).json" />
		<add key="a2"
             value="ControlCases\Acceleration\Acceleration_2_XY_(30, -15).json" />

		 <!-- Deceleration -->
		<add key="d1"
             value="ControlCases\Deceleration\Deceleration_1_XY_(2, -3.json" />
		<add key="d2"
             value="ControlCases\Deceleration\Deceleration_2_XY_(30, -15).json" />

		<!-- ////////////////////////////////////////////////////////////// -->
		<!-- The root output directory (relative to working directory) -->
		<add key="RootOutputDir" value="ControlNetOutput" />

		<!-- ////////////////////////////////////////////////////////////// -->
		<!-- Absolute path of Python exe file -->
		<!-- <add key="Python"
              value="...\AppData\Local\Programs\Python\Python310\python.exe" /> -->
	</appSettings>
</configuration>

基本飞行模式控制

现在我们将考虑飞行器的一些基本飞行模式，它们构成了其运动轨迹。

稳定

此处，“稳定”意味着将飞行器从任何当前状态（非零初始角度/角速度和/或平移速度）引导到悬停状态。对最终悬停点没有严格要求，假定该点将在初始位置的“一定范围内”。

稳定性的数值结果如下。

稳定 1

这是从非零初始角度状态进行稳定的案例。

采样间隔 Δt（JSON 配置文件中为 dt）= 0.1 秒，
间隔数 N = 61，
迭代次数（配置中为 maxIterations）= 2。

  x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12
  φ dφ/dt θ dθ/dt ψ dψ/dt x dx/dt 是 dy/dt z dz/dt
单位 rad 弧度/秒 rad 弧度/秒 rad 弧度/秒 m 米/秒 m 米/秒 m 米/秒
xinit 0.2 0 0.2 0 0.2 0 0 0 0 0 0 0
期望 r 0 0 0 0 0 0 0 0 0 0 0 0
diag(Q)1 1 1 1 1 1 1 1 1 1 1 1 1
diag(Q)2 10 1 10 1 10 1 10 1 10 1 10 1

期望 u = 0，
Z = 0

结果 for diag(Q)1: 从下面的瞬态图可以看出，获得的控制策略使四轴飞行器在 5 秒内稳定下来，位移（x: 0.25 米, y: -0.19 米, z: 0 米）偏离其初始位置。

Stabilization 1, Displacements
Stabilization 1, Velocities
Stabilization 1, Angles

稳定 2

这是从具有非零角度以及非零角速度和平移速度的初始状态进行稳定的情况。

采样间隔 Δt（JSON 配置文件中为 dt）= 0.1 秒，
间隔数 N = 61，
迭代次数（配置中为 maxIterations）= 2。

  x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12
  φ dφ/dt θ dθ/dt ψ dψ/dt x dx/dt 是 dy/dt z dz/dt
xinit 0.3 1 -0.4 1 0.2 1 0 1 0 1 0 -1
期望 r 0 0 0 0 0 0 0 0 0 0 0 0
diag(Q)1 1 1 1 1 1 1 1 1 1 1 1 1
diag(Q)2 10 1 10 1 10 1 10 1 10 1 10 1

期望 u = 0，
Z = 0

结果 for diag(Q)2: 所得控制策略使四轴飞行器在 3 秒内稳定下来，位移（x: -0.02 m, y: -0.14 m, z: 0 m）偏离其初始位置。

Stabilization 2, Displacements
Stabilization 2, Velocities
Stabilization 2, Angles

过渡

这是从初始悬停点到最终悬停点的过渡。

在本节中，我们将使用施加在飞行器上的引力（飞行器重量）值

M · g = 0.65 kg · 9.81 m/s2 = 6.3765 N

过渡 1

将飞行器从初始悬停点移动到最终悬停点（x = 10 米，y = -1 米，z = 1 米）。

在这种情况下，我们将期望状态设置为期望的最终位置：r7 = 10，r9 = -1，r11 = 1。

采样间隔 Δt（JSON 配置文件中为 dt）= 0.1 秒，
间隔数 N = 101，
迭代次数（配置中为 maxIterations）= 2。

  x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12
  φ dφ/dt θ dθ/dt ψ dψ/dt x dx/dt 是 dy/dt z dz/dt
单位 rad 弧度/秒 rad 弧度/秒 rad 弧度/秒 m 米/秒 m 米/秒 m 米/秒
xinit 0 0 0 0 0 0 0 0 0 0 0 0
期望 r 0 0 0 0 0 0 10 0 -1 0 1 0
diag(Q) 100 10 100 10 100 10 1 1 1 1 1 1

 

  m1 m2 m3 m4
期望 u M · g = 6.3765 0 0 0
diag(Z) 1 0 0 0

结果： 所得控制策略使四轴飞行器在 8 秒后悬停在指定点。

Transition 1, Displacements
Transition 1, Velocities
Transition 1, Angles

过渡 2

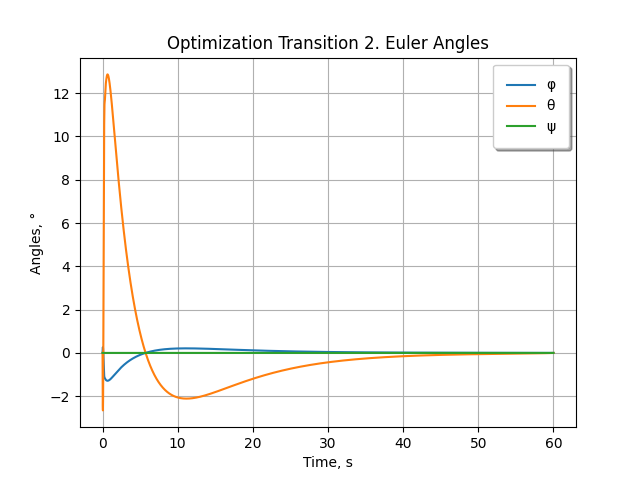
将飞行器从初始悬停点移动到最终悬停点（x = 100 米，y = 10 米，z = 20 米）。

采样间隔 Δt（JSON 配置文件中为 dt）= 0.1 秒，
间隔数 N = 601，
迭代次数（配置中为 maxIterations）= 2。

  x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12
  φ dφ/dt θ dθ/dt ψ dψ/dt x dx/dt 是 dy/dt z dz/dt
单位 rad 弧度/秒 rad 弧度/秒 rad 弧度/秒 m 米/秒 m 米/秒 m 米/秒
xinit 0 0 0 0 0 0 0 0 0 0 0 0
期望 r 0 0 0 0 0 0 100 0 10 0 20 0
diag(Q) 1000 1 1000 1 1000 1 0.01 1 0.01 1 0.01 1

 

  m1 m2 m3 m4
期望 u M · g = 6.3765 0 0 0
diag(Z) 1 0 0 0

结果：所得到的控制策略使四轴飞行器在 60 秒后悬停在指定点。

Transition 2, Displacements
Transition 2, Velocities
Transition 2, Angles

加速

这是从初始悬停点加速到恒定水平速度。

加速 1

将飞行器从初始悬停点加速到水平速度（dx/dt = 2 m/s，dy/dt = -3 m/s）。

采样间隔 Δt（JSON 配置文件中为 dt）= 0.1 秒，
时间间隔数 N = 51，
迭代次数（配置中为 maxIterations）= 2。

  x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12
  φ dφ/dt θ dθ/dt ψ dψ/dt x dx/dt 是 dy/dt z dz/dt
单位 rad 弧度/秒 rad 弧度/秒 rad 弧度/秒 m 米/秒 m 米/秒 m 米/秒
xinit 0 0 0 0 0 0 0 0 0 0 0 0
期望 r 0 0 0 0 0 0 0 2 0 -3 0 0
diag(Q) 0 1 0 1 0 1 0 1 0 1 10 1

期望 u = 0，
Z = 0

结果： 所得控制策略使四轴飞行器在 3 秒后以规定的水平速度移动。

Acceleration 1, Displacements
Acceleration 1, Velocities
Acceleration 1, Angles

加速 2

将飞行器从初始悬停点加速到水平速度（dx/dt = 30 m/s，dy/dt = -15 m/s）。

采样间隔 Δt（JSON 配置文件中为 dt）= 0.1 秒，
间隔数 N = 201，
迭代次数（配置中为 maxIterations）= 2。

  x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12
  φ dφ/dt θ dθ/dt ψ dψ/dt x dx/dt 是 dy/dt z dz/dt
单位 rad 弧度/秒 rad 弧度/秒 rad 弧度/秒 m 米/秒 m 米/秒 m 米/秒
xinit 0 0 0 0 0 0 0 0 0 0 0 0
期望 r 0 0 0 0 0 0 0 30 0 -15 0 0
diag(Q) 1 1 1 1 1 1 0 0.001 0 0.001 10 0.001

期望 u = 0，
Z = 0

结果： 所得控制策略使四轴飞行器在 17 秒后以规定的水平速度移动。

Acceleration 2, Displacements
Acceleration 2, Velocities
Acceleration 2, Angles

减速

这是从初始恒定水平速度减速到悬停状态。此机动与上述加速相反。

减速 1

使飞行器从具有水平速度（dx/dt = 2 m/s，dy/dt = -3 m/s）的初始状态减速至最终悬停点（与加速 1 案例相反）。

采样间隔 Δt（JSON 配置文件中为 dt）= 0.1 秒，
时间间隔数 N = 51，
迭代次数（配置中为 maxIterations）= 2。

  x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12
  φ dφ/dt θ dθ/dt ψ dψ/dt x dx/dt 是 dy/dt z dz/dt
单位 rad 弧度/秒 rad 弧度/秒 rad 弧度/秒 m 米/秒 m 米/秒 m 米/秒
xinit 0 0 0 0 0 0 0 2 0 -3 0 0
期望 r 0 0 0 0 0 0 0 0 0 0 0 0
diag(Q) 1 1 1 1 1 1 1 1 1 1 10 1

期望 u = 0，
Z = 0

结果： 所得控制策略使四轴飞行器在 5 秒内从初始水平速度减速至悬停，相对于减速开始点，位移为 (x: 0.22 m, y: -0.32 m, z: 0 m)。

Deceleration 1, Displacements
Deceleration 1, Velocities
Deceleration 1, Angles

减速 2

使飞行器从初始状态（水平速度为（dx/dt = 30 m/s，dy/dt = -15 m/s））减速至最终悬停点（与加速 2 案例相反）。

采样间隔 Δt（JSON 配置文件中为 dt）= 0.1 秒，
间隔数 N = 201，
迭代次数（配置中为 maxIterations）= 2。

  x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12
  φ dφ/dt θ dθ/dt ψ dψ/dt x dx/dt 是 dy/dt z dz/dt
单位 rad 弧度/秒 rad 弧度/秒 rad 弧度/秒 m 米/秒 m 米/秒 m 米/秒
xinit 0 0 0 0 0 0 0 30 0 -15 0 0
期望 r 0 0 0 0 0 0 0 0 0 0 0 0
diag(Q) 1 5 1 5 1 5 0 0.01 0 0.01 10 0.01

期望 u = 0，
Z = 0

结果： 所得控制策略使四轴飞行器在 12 秒内从其初始水平速度减速至悬停，相对于减速开始点，位移为 (x: 64 m, y: -27.5 m, z: 0 m)。

Deceleration 2, Displacements
Deceleration 2, Velocities
Deceleration 2, Angles

对我们刚刚计算的控制策略应用到具有相同初始平移速度，但非零初始角度和角速度的情况的模拟。下表提供了相应的值，随后是瞬态图。

  x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12
  φ dφ/dt θ dθ/dt ψ dψ/dt x dx/dt 是 dy/dt z dz/dt
单位 度 度/秒 度 度/秒 度 度/秒 m 米/秒 m 米/秒 m 米/秒
xinit
用于优化		 0 0 0 0 0 0 0 30 0 -15 0 0
xinit
用于模拟		 20 -20 15 -15 -20 20 0 30 0 -15 0 0

 

Deceleration 2, Displacements
Deceleration 2, Velocities
Deceleration 2, Angles

讨论

我们知道，没有算法对所有情况都是完美的，特别是对于非线性动态系统。这里没有万能药。尽管我们通过单一技术在不同机动中取得了一些有希望的结果，但可能改进和进一步工作的清单是无穷无尽的。

所提出的解决方案意味着来自状态向量所有坐标的反馈（尽管在某些模式下我们得到了某些坐标的零反馈）。在实际系统中，并非所有这些坐标都可以直接测量。因此，应该使用一些众所周知的方法来估计不可用坐标，例如卡尔曼滤波。将我们得到的闭环控制系统视为内部回路的级联控制应用可能有助于提高系统的鲁棒性。作为级联控制的一个特例，可以考虑在控制通道中添加积分器的众所周知技术。应该使用更真实的四轴飞行器动态模型。该控制技术可以与飞行器定位（特别是为此目的使用摄像头）、无人机编队管理等结合使用。

LQR 和 ILQR 可以被视为机器学习 (ML) 的一个案例——基于模型的强化学习。与 ML 中常见的情况一样，计算结果显示了受控系统的特征，否则无法理解。对于我们的四轴飞行器模型，足够的轨迹迭代次数是 2。期望向量和权重矩阵的选择是数值实验的结果，而不是理论分析。权重矩阵 Q 和 Z 中权重系数的选择反映了相对于期望值的缩放。对开环系统离散传递矩阵 Fk 和 Hk [1](5) 以及结果反馈矩阵 LN-k 和闭环系统输入向量 cN-k [1](7)（其中 k = 0, 1, ..., N - 1）的彻底检查可以极大地促进对系统动力学的理解。如上所述，在某些飞行模式下，这种分析可能会建议将整个动态系统分解为相对独立的单输入子系统，并且仅从状态向量 x 的少数坐标获得反馈。所描述的技术可以用于训练神经网络 (NN)，该网络生成飞行控制器参数，例如反馈增益和闭环系统输入。

结论

这项工作展示了我的文章 [1] 中提供的技术在四轴飞行器控制中的应用。在 ILQR 意义上最优的控制策略是为飞行器的稳定、过渡、加速和减速等飞行模式自动生成的。更新后的软件即时生成瞬态图。

历史

  • 2022年6月17日：初始版本

谢谢

感谢 Sergey Rubinsky 博士对本文主题的有益讨论和宝贵建议。

© . All rights reserved.