单词转换矩阵向量 Hat 算法 Python

Python 和 NumPy 中用于近似字符串匹配的最优 Wagner-Fischer 算法

Arthur V. Ratz

5.00/5 (10投票s)

2022 年 9 月 17 日

CPOL

27分钟阅读

11911

107

使用 Wagner-Fischer（基于两行矩阵）算法有效地计算字面字符串的 Levenshtein 距离。

下载 wfsch_levdist_numpy.zip - 224.4 KB

引言

“编辑距离的概念及其计算的高效算法在拼写纠错问题中有明显的应用，并且可能有助于在编程语言设计中选择相互距离不同的关键字。” - R.A. Wagner, M.J. Fischer, MIT, 1974 年 1 月。

近似字符串匹配是许多数据分析算法中的一项基本技术，它能够确定各种文本数据之间的相似性。大多数情况下，相似性以两个字面字符串之间距离的数值形式表示。

近似字符串匹配在许多现有的 Web 和移动应用程序的拼写检查器和单词自动完成功能中都有应用，为单词输入错误或其他不正确的用户输入提供正确的单词建议。拼写检查器的全文本搜索引擎会计算用户输入与数据库中每个正确字符串之间的距离，找到相似度最高的单词，即距离最小的单词。

各种经典的距离度量，例如 Sørensen 指数和 Hamming 距离，被用于确定文本数据的相似性。然而，使用这些度量最终会导致错误的建议，这是由这些相似字符串计算之间的误导性距离引起的。应用于字面字符串时，Hamming 距离和其他度量不考虑共同子串（后缀）和相邻字符的转置，它们会计算最相似字符串之间的最大距离。

1965 年，Vladimir Levenshtein 证明，可以通过计算将失真字符串转换为正确字符串所需的最小单字符编辑操作次数来评估字符串之间的距离。Levenshtein 距离度量被公式化为 Levenshtein 自动机算法。它被用作 Hamming 码的替代方法，用于从损坏或失真的二进制流中恢复正确的字节。

Levenshtein 距离是一种非常流行的数据分析算法，用于广泛的应用，完全解决了文本数据相似性评估问题，能够识别共同子串和相邻字符的转置。

存在一整类算法来计算 Levenshtein 距离，包括 Wagner-Fischer 算法的两种变体，以及由 D.S. Hirschberg 于 1975 年提出的用于评估相似性和最优字符串对齐的 Hirschberg 算法。

本文详细讨论了最优 Wagner-Fischer（基于两行矩阵）算法及其实现。Python 代码示例演示了如何使用 Wagner-Fischer 算法计算密歇根大学“英语单词列表”（https://www-personal.umich.edu/~jlawler/wordlist.html）数据集中（包含超过 60,000 个按字母顺序排序的英语单词）的各种字符串的 Levenshtein 距离。

Levenshtein 距离

Levenshtein 距离是用于有效评估两个字面字符串距离和相似性的度量。它仅仅依赖于将距离表示为将第一个字符串转换为第二个字符串所需的最小编辑操作次数，而不是两个字符串中未匹配字符的统计信息。

显然，一个字符串通过一系列删除、插入和替换第一个字符串中的字符来转换为另一个字符串。结果是，两个不相似的字符串通过大量编辑来转换，而最相似的字符串则通过较少数量的编辑来转换。

Levenshtein 距离的主要优点是，在评估字符串相似性时，它会考虑到两个字符串可能具有共同的子串，因此，这些字符串之间的实际距离小于 Hamming 距离或其他距离。此外，Levenshtein 距离是基于获取需要删除、插入或替换的字符数量来计算的，而无需执行字符串本身的转换。

在两个字符串没有共同子串（后缀）的情况下，Levenshtein 距离和 Hamming 距离是相等的。否则，Levenshtein 距离的计算会考虑到共同子串，这些子串在两个字符串中的位置未匹配，因为它只能通过转换的最小编辑次数来评估这些字符串的距离。

两个长度不同（$|a|$ 和 $|b|$）的字符串 $a$ 和 $b$ 之间的 Levenshtein 距离由如下分段函数 $\mathcal{Lev}(a,b)$ 给出

$\mathcal{L}(a,b) = \begin{cases} |a| &\text{, 如果 } |b| = 0\\ |b| &\text{, 如果 } |a| = 0\\ \mathcal{L}(tail(a),tail(b)) &\text{, 如果 } a[0] = b[0]\\ min \begin{cases} \mathcal{L}(tail(a),b) &\text{删除}\\ \mathcal{L}(a,tail(b)) &\text{插入}\\ \mathcal{L}(tail(a),tail(b)) &\text{替换}\\ \end{cases} &\text{, 否则} \end{cases}$

这里，两个字符串的距离计算主要涉及字符串的尾部 $\textbf{tail}(a)$ 和 $\textbf{tail}(b)$。$\textbf{tail}(a)$ 是除字符串 $a$ 的第一个字符外的所有字符组成的字符串。例如：获得每个下一个 i-th $\textbf{tail}(a)$ 会得到一个新字符串，其中包含 $a$ 中剩余的所有字符，然后是 $a[i]$ 字符。将 $\textbf{tail}(a)$ 与字符串 $b$ 在第一个字符处匹配，会导致从字符串 $a$ 的开头删除一个字符。类似地，通过将字符串 $a$ 与 $\textbf{tail}(b)$ 匹配，分别完成一个字符向字符串 $a$ 末尾的插入。同样，将 $a[0]$ 与 $b[0]$ 替换一个字符，是向前移动到下一个 $\textbf{tail}(a+1)$ 和 $\textbf{tail}(b+1)$ 字符串的第一个字符。特定的编辑是通过将其中一个字符串 $a$ 或 $b$，或两者都与两个字符串中的第一个字符位置对齐来实现的，以便每个对齐都导致字符串 $a$ 转换为 $b$。

在递归计算 Levenshtein 距离时，分段函数处理第一个字符相等、不相等，或者字符串长度 $|a|$ 或 $|b|$ 等于 $0$ 的情况。计算从第一个字符 $a[0]$ 和 $b[0]$ 开始。如果字符 $a[0]$ = $b[0]$ 相等，则继续处理下一个 $\textbf{tail}(a+1)$ 和 $\textbf{tail}(b+1)$ 字符串对，因为当 $\textbf{tail}(a)$ 和 $\textbf{tail}(b)$ 的第一个字符相等并在其位置匹配时，不需要进行任何编辑。否则，如果 $a[0]$ != $b[0]$，则递归地将相同的分段函数 $\mathcal{Lev}(a,b)$ 应用于每个字符串，分别是 $\mathcal{Lev}(\textbf{tail}(a),b)$、$\mathcal{Lev}(a,\textbf{tail}(b))$、$\mathcal{Lev}(\textbf{tail}(a),\textbf{tail}(b))$。直到第一个字符 $a[0]$ 和 $b[0]$ 最终匹配为止，才进行每个字符串对的距离计算。递归调用的分段函数会累积 $a$ 中删除、插入和替换字符的计数，将相应的编辑计数加 $1$。字符串 $\textbf{tail}(a)$ 和 $\textbf{tail}(b)$ 之间的 Levenshtein 距离被评估为这些计数的最小值。它从这些尾部开始进行距离计算，其中编辑次数最少。在字符串长度 $|a|$ 或 $|b|$ 为 $0$ 的情况下，分段函数返回非零长度，因为 $a$ 到 $b$ 的字符串转换需要将剩余的字符插入字符串 $a$ 中，其数量等于非空字符串的长度。最后，当两个字符串 $a$ 和 $b$ 的长度都为 $0$ 时，计算结束，分段函数 $\mathcal{Lev}(a,b)$ 的值为计算出的完整字符串 $a$ 和 $b$ 的 Levenshtein 距离。

Levenshtein 分段函数在大多数编程语言（如 Haskell、Python 等）中都有一个简单的实现。然而，它会由于相同子串的重复计算而导致递归深度不断增加，因此不能有效地用作计算算法。

最优 Wagner-Fischer 算法

1974 年，R. A. Wagner 和 M. J. Fischer 提出了一种更好的 Levenshtein 距离算法。它基于矩阵 M 计算两个完整字符串 $S_{1}$ 和 $S_{2}$ 的 Levenshtein 距离，该矩阵存储了 $S_{1}$ 的每个 $i$-字符前缀和 $S_{2}$ 的每个 $j$-字符前缀之间的最小距离 $M[i][j]$。Wagner-Fischer 算法是一种动态规划算法，其中 Levenshtein 距离计算被分解为多个子问题，计算 $S_{1}$ 和 $S_{2}$ 字符串的前缀（即“较小”的子串）之间的相同最小距离。

该算法主要处理两个字符串的 $i$-和 $j$-字符前缀对 $S_{1}[0..|i|]$ 和 $S_{2}[0..|j|]$，而不是后缀或字符串尾部。具体来说，字符串 $S$ 的 $i$-字符前缀是 $S[i]$-字符的初始段，后跟字符串的前 $i$ 个字符。下面图示了 $S_{1}$ 和 $S_{2}$ 字符串的 $i$-和 $j$-字符前缀。

前缀长度 $|i|=i+1$ 是 $S$ 的前 $i$ 个字符的计数，包括前缀字符 $S[i]$。此外，在两个字符串的第一个字符 $S_{1}[0]$ 和 $S_{2}[0]$ 的位置都插入了一个“空”的 1 字符前缀 **（ # ）**。

S₁ 到 S₂ 字符串转换

与 Levenshtein 递归分段函数类似，Wagner-Fischer 算法基于每个前缀 $S_{1}[i]$ 到 $S_{2}[j]$ 转换的删除、插入和替换计数来计算 Levenshtein 距离。

从逻辑上讲，这些编辑操作中的每一个都与通常的略有不同

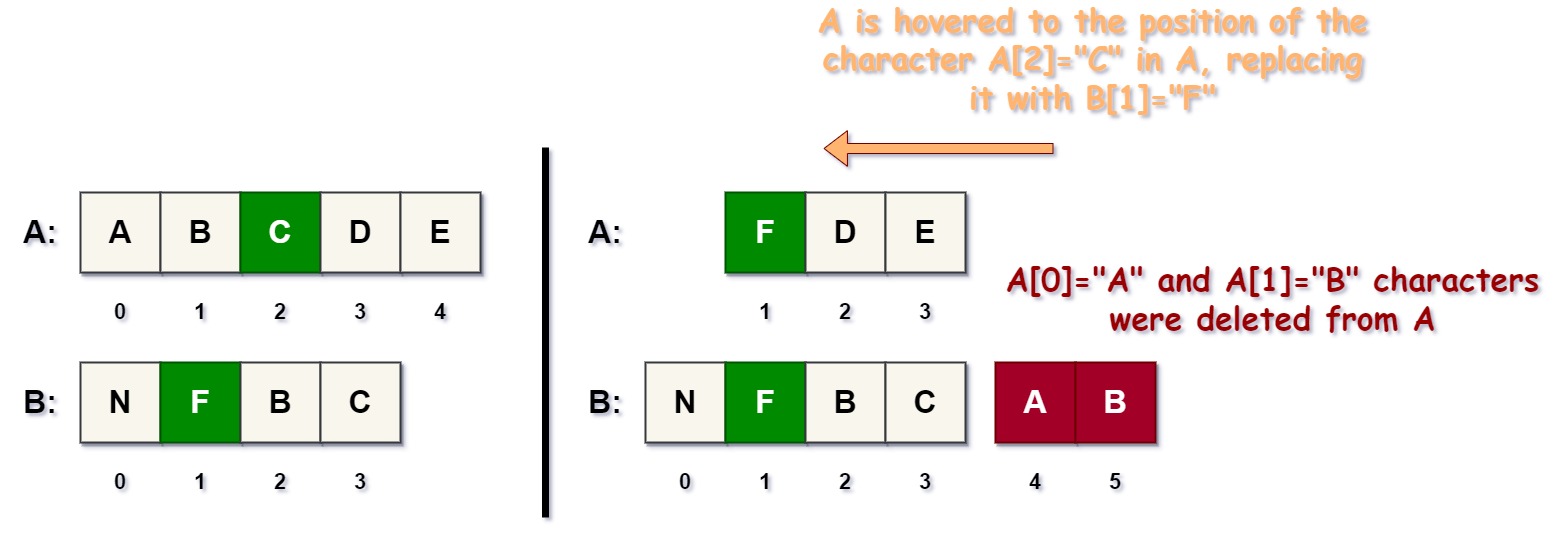
**从 S₁ 删除，插入到 S₂：** 从 $S_{1}$ 字符串的开头删除的字符数，并将其插入到 $S_{2}$ 字符串的末尾。这个数字是 $S_{1}[i]$ 到 $S_{2}[j]$ 转换的删除计数。

如果长度 $|i|$ 小于 $|j|$，即 $|i| < |j|$，则前缀 $S_{1}[i]$ 无法通过一系列插入来转换为 $S_{2}[j]$，其计数为 $0$。此后，为了找到 $S_{1}[i]$ 到 $S_{2}[j]$ 转换的最小编辑距离，将使用之前的最小距离。

**插入到 S₁，从 S₂ 删除：** 通过删除 $S_{2}$ 开头的每个字符（包括空前缀 **（ # ）**）并将它们添加到 $S_{1}$ 的末尾来完成插入到 $S_{1}$ 的操作。插入计数是插入到 $S_{1}$ 并分别从 $S_{2}$ 删除的字符数。

同样，当 $S_{1}[i]$ 的前缀长度 $|i|$ 大于 $S_{2}[j]$ 的前缀长度 $|j|$，即 $|i| > |j|$ 时，前缀 $S_{1}[i]$ 无法通过插入编辑转换为 $S_{2}[j]$，其计数为 $0$。此类转换的距离 $M[i][j]$ 是根据矩阵 M 中的先前距离之一获得的。

**替换 S₁[i] 为 S₂[j]：** 仅当 $S_{1}[i]$ 和 $S_{2}[j]$ 的字符位置在两个字符串中都匹配（$i = j$）时才进行替换。在这种情况下，替换计数是 $S_{1}$ 的删除或插入次数，使得字符 $S_{1}[i]$ 和 $S_{2}[j]$ 最终出现在 $S_{1}$ 和 $S_{2}$ 的相同位置。如果字符 $S_{1}[i]$ 和 $S_{2}[j]$ 在其相等的位置时不相等，则将 $1$ 加到删除或替换计数中，因为已进行了一次 $S_{1}[i]$ 到 $S_{2}[j]$ 的字符替换。

存储在矩阵 M 中的距离值

字符串 $S_{1}$=ABCDE 和 $S_{2}$=NFBC 的 Levenshtein 距离计算结果为形状为 $(5\times{4})$ 的距离矩阵 M，如下所示。

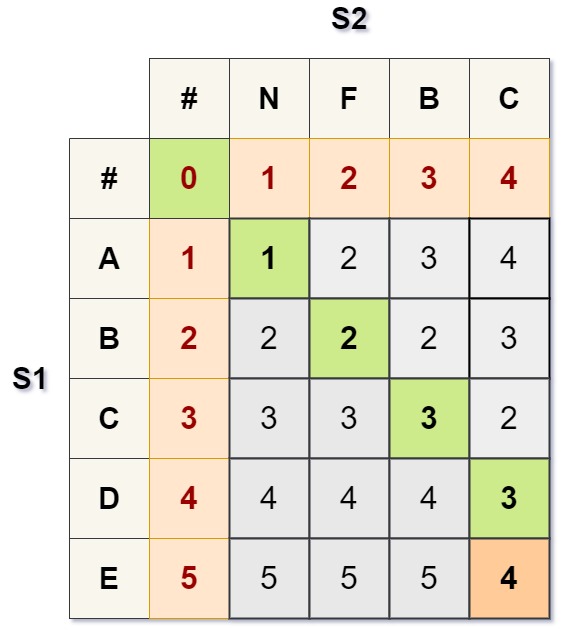
矩阵 $M$ 中的距离值排列方式使得每个 $i$-字符前缀 $S_{1}[i]$ 都映射到所有相应的 $j$-字符前缀 $S_{2}[j]$，并且值 $M[i][j]$ 分别是相应前缀之间的距离。矩阵中第 $0$ 列和第 $0$ 行的值是空字符串 **（ # ）** 与 $S_{1}[i]$ 或 $S_{2}[j]$ 的每个前缀之间的最小距离 **（红色）**。由于第一个字符 **（ # ）** 被插入到两个字符串的开头，因此 $S_{1}$ 和 $S_{2}$ 中的字符位置是零基索引的，而 M 中的前缀索引是单基索引的。

矩阵 $M$ 中存储了三种基本类型的距离，它们的取值是相应前缀 $S_{1}[i]$ 和 $S_{2}[j]$ 转换的字符删除、插入和替换计数。删除计数是矩阵对角线下方的 **（深灰色）** 值，插入计数是其对角线上方的 **（浅灰色）** 值，而替换计数是沿着矩阵 $M$ 对角线的 **（绿色）** 值。

初始化

Wagner-Fischer 算法仅基于这样的观察：Levenshtein 距离的“从底向上”计算只有在最初提供了从“空”字符串 $S_{1}$ 或 $S_{2}$ 到另一个字符串的所有前缀的距离时才可能。每个距离都是必须从空字符串 **（ # ）**、$S_{1}$ 或 $S_{2}$ 删除或插入的字符数，将其转换为 $S_{2}[j]-$ 或 $S_{1}[i]$-前缀，分别。

因此，M 的第 1 列分配给 $S_{1}[i]$-前缀与空 $S_{2}$ = **（ # ）** 字符串之间的距离 $M[0..|S_{1}|)[0] = 0,1,2,3,...,|S_{1}|$。每个距离都是从 $S_{1}[i]$-前缀中删除的字符数，以便最终将其转换为空字符串 **（ # ）**。显然，这种删除次数等于 $S_{1}[i]$-前缀的长度 $|i|$，最初已提供。类似地，M 的第 1 行用从空字符串 $S_{1}$ = **（ # ）** 到 $S_{2}[j]$-前缀的距离 $|j|$，$M[0][0..|S_{2}|) = 0,1,2,3,...,|S_{2}|$ 进行初始化，分别。

S₁ 和 S₂ 的 Levenshtein 距离计算

一旦定义了形状为 $(|S_{1}|\times{|S_{2}|})$ 的距离矩阵 $M$，它就逐行计算 Levenshtein 距离，用 $i$-th 字符前缀 $S_{1}[i], i=[1..|S_{1}|) $ 到 $S_{2}[j], j=[1..|S_{2}|) $ 的所有前缀的距离填充 M 的每个 $i$-th 行，直到最后的距离值 $M[|S_{1}| - 1][|S_{2}| - 1]$ 成为 $S_{1}$ 和 $S_{2}$ 完整字符串的 Levenshtein 距离。相应前缀 $S_{1}[i]$ 和 $S_{2}[j]$ 之间的距离 $M[i][j]$ 的计算由以下表达式给出：

$M[i][j] = min \begin{cases} M[i-1][j] + 1 &\text{, 删除}\\ M[i][j-1] + 1 &\text{, 插入}\\ M[i-1][j-1]+1_{(S1[i]\neq{S2[j]})} &\text{, 替换}\\ \end{cases}$

上面的表达式通过计算先前为其他前缀计算出的距离的最小值来计算前缀 $S_{1}[i]$ 和 $S_{2}[j]$ 之间的距离 $M[i][j]$。每个距离都精确地对应于对 $S_{1}$ 字符串进行的删除、插入和替换的次数。

$M[i-1][j] + 1$	从 S₁ 删除，插入到 S₂
$M[i][j-1] + 1$	插入到 S₁，从 S₂ 删除
$M[i-1][j-1] + 1_{(S_{1}[i]\neq{S_{2}[j]})}$	替换 S₁[i] 为 S₂[j]

Levenshtein 距离计算从两个字符串的第一个前缀 $S_{1}[1]$ 和 $S_{2}[1]$ 的距离值 $M[1][1]$ 开始，将上述表达式应用于 $S_{1}$ 和 $S_{2}$ 的所有前缀组合，直到计算出最长前缀之间的距离 $M[|S_{1}| - 1][|S_{2}| - 1]$，即被评估的 Levenshtein 距离。

根据动态规划方法，矩阵 $M$ 被分成多个 $(2\times{2})$ 形状的“小”子矩阵。每个子矩阵的值是删除的字符数 $M[i-1][j]+1$ **（红色）**，插入的字符数 $M[i][j-1]+1$ **（蓝色）** 和替换的字符数 $M[i-1][j-1]+1$ **（绿色）**。

前缀 $S_{1}[i]$ 和 $S_{2}[j]$ 之间的距离 $M[i][j]$ 计算为上述计数的最小值。最后一个子矩阵中的值 $M[i][j]$ 是被评估的 Levenshtein 距离。

最后，Wagner-Fischer 算法的平均复杂度（时间）和空间复杂度为 $\theta(|S_{1}|\times{|S_{2}|})$，尽管存在更优化的算法变体。

迭代式两行矩阵算法

然而，可以通过不计算完整的距离矩阵 M 来评估相同的 Levenshtein 距离。每个前缀 $S_{1}[i]$ 和 $S_{2}[j]$ 的距离计算仅基于矩阵当前 $i$-行和前一 $(i-1)$-行的值，因此，其他行的值可以简单地丢弃。这提供了将算法使用的空间显着减少到 O(2 x |S₂|) 的能力。

Wagner-Fischer（两行矩阵）算法的伪代码如下所示。

\( \textbf{算法 }\text{Wagner-Fischer}(S_{1},S_{2})\textbf{ 是：}\\ \hspace{28pt} \textbf{声明： } \textrm{V}_{old}[0..|S_{2}|) = \{0\} \textbf{ 作为 } \textrm{整数}\\ \hspace{73pt} \textrm{V}_{new}[0..|S_{2}|) = \{0\} \textbf{ 作为 } \textrm{整数}\\\ \\ \hspace{28pt} \textbf{输出： } \mathcal{L} - S_{1}\textit{ 和 }S_{2}\textit{ 的 Levenshtein 距离}\\\ \\ \hspace{28pt} \textbf{初始化： } \textrm{V}_{old}[0..|S_{2}|) \textit{ 向量，带有“插入”距离 }\\ \hspace{85pt} \textit{从 1-前缀 (#) 到 } S_{2}[0..|j|), j=[0..|S2|)\textit{ 的每个前缀}\\ \hspace{28pt} \textbf{对于每个 } \textit{i} \in{ [0..|S_{1}|)} \textbf{ do: } \textrm{V}_{old}[i] = i\\\ \\ \hspace{28pt} \textbf{对于 } \textit{i} \gets{1} \textbf{ 到 } |S_{1}| \textbf{ do: }\\ \hspace{46pt} \textrm{V}_{new}[0] = i;\\ \hspace{43pt} \textrm{V}_{new}[1..|S2|) = 0\\ \hspace{46pt} \textbf{对于 } \textit{j} \gets{1} \textbf{ 到 } |S_{2}| \textbf{ do: }\\ \hspace{65pt} \textit{rCost} = 1 \textbf{ 如果 } S_{1}[i-1]\neq{S_{2}[j-1]} \textbf{ 否则： } 0 \\ \hspace{65pt} \textit{del} = \textrm{V}_{old}[j] + 1\\ \hspace{65pt} \textit{ins} = \textrm{V}_{new}[j - 1] + 1\\ \hspace{65pt} \textit{rep} = \textrm{V}_{old}[j - 1] + \textit{rCost}\\\ \\ \hspace{65pt} \textrm{V}_{new}[j] = \textbf{minimum}(del,ins,rep)\\\ \\ \hspace{46pt} \textrm{V}_{old} \gets{\textrm{V}_{new}}\\\ \\ \hspace{28pt} \mathcal{L} \gets{V_{old}[|S_{2}|-1]}\\\ \\ \hspace{28pt} \textbf{返回： } \mathcal{L} \)

该算法声明两个向量 $V_{old}$ 和 $V_{new}$，在下面的特定 Python 代码示例中分别称为 e_d 和 e_i。向量 $V_{old}$ 用必须插入到空 $S_{1}$ 字符串（ # ）中以将其转换为字符串 $S_{2}$ 的字符数进行初始化。

对于每个 i-th 前缀 $S_{1}[i], i=[1..|S_{1}|)$，它初始化第二个向量 $V_{new}$，将第一个值 $V_{new}[0]$ 分配给从 $S_{1}$ 删除的字符数以将其转换为空字符串（ # ） $S_{2}$，而 $V_{new}$ 向量的所有其他值最初为 0。在每次迭代中，它会计算 $i$-th 前缀 $S_{1}[i]$ 和 $S_{2}[j], j=[1..|S_{2}|)$ 的所有前缀之间的距离 $V_{new}[j]$，这些距离存储在 $V_{new}$ 向量中。由于 $V_{new}$ 中的所有这些值都已计算完毕，它会用从 $V_{new}$ 向量复制的值更新 $V_{old}$ 向量，然后继续计算所有下一个 $(i+1)$-th 前缀 $S_{1}[i+1]$ 的距离，直到计算出从最后一个前缀 $S_{1}[|S_{1}|-1]$ 的距离。相应 $V_{new}[|S_{2}|-1]$ 向量中的最后一个值是完整 $S_{1}$ 和 $S_{2}$ 字符串的 Levenshtein 距离。

一个例子...

假设失真字符串和正确字符串分别为 $S_{1}$ = **ADVBBR** 和 $S_{2}$ = **ADVERBS**。失真字符串 $S_{1}$ 和正确字符串 $S_{2}$ 都具有相同的 PREDIX **ADV…**。同样，$S_{2}$ 中的相邻字符 **R**、**B** 在失真字符串 $S_{1}$ 中被转置为 **B**、**R**，并且失真字符串 $S_{1}$ 缺少正确字符串 $S_{2}$ 中的字符 **E** 和 **S**。

字符串 $S_{1}$ 和 $S_{2}$ 的完整字符串 Levenshtein 距离评估从两个字符串的相应字符前缀 $S_{1}[1]= S_{2}[1] =$ **A** 开始，并计算最小编辑距离 $M[1][1]$。由于两个前缀 **A** 相同，并且在 $S_{1}$ 中匹配相同位置，因此不进行任何替换，其计数为 $0$。否则，当两个字符串的第一个字符前缀不相同时，$S_{1}[1]\neq{S_{2}[1]}$，并且需要将 $S_{1}[1]$ 替换为 $S_{2}[1]$ 时，替换计数为 $1$。这里，前缀 **A** 后面跟着另一个“空”前缀 **（ # ）**，并且需要删除和插入一个字符到 $S_{1}$ 来将前缀 **A** 更改为 **（ # ）**，以及将 **（ # ）** 更改为 **A**，分别在 $S_{1}$ 或 $S_{2}$ 字符串中。由于删除、插入和替换计数已预先提供，因此无需进行这些计数的计算。最后，这些计数的最小值是距离值 $M[1][1] = min(1,1,0) = 0$，当第一个前缀 $S_{1}[1] = S_{2}[1]$ 相等时，以及 $M[1][1] = min(1,1,1) = 1$，除非另有说明。

在 $S_{2}$ 的前缀 **A** 之后，计算前缀 $S_{1}[1]$ = **A** 和 $S_{2}[2]$ = **D** 的最小编辑距离 $M[1][2]$。

在这里，插入计数等于 $2$，因为需要 2 次插入（蓝色）字符 **（ # ）**、**A**（从 $S_{2}$ 删除），以匹配 $S_{1}$ 中 **A** 位置的字符 **A** 和 **D**。

同样，将字符 **A** 替换为 **D** 的替换计数等于 $1$，因为只需要向 $S_{1}$ 末尾插入一次字符即可将前缀 **A** 更改为 $S_{1}$ 中的 **D**。

在这种情况下，对于前缀 **A** 和 **D**，没有删除计数，因为无法通过从 $S_{1}$ 删除字符来将 **A** 转换为 **D**。因此，删除计数是前面得到的相等前缀 **A** 之间的最小编辑距离 $M[1][1]$ = $0$。

最后，观察到空前缀 **（ # ）** 的长度，在删除、插入和替换计数中分别加 $1$，然后得到这两个前缀 **A** 和 **D** 之间的最小编辑距离 $M[1][2]$，其值为这些计数的最小值，即 $M[1][2] = min(1,3,2) = 1$。

对于 $S_{1}[1] = $ **A** 和 $S_{2}[3] =$ **V** 前缀之间的最小距离 $M[1][3]$ 的计算，应用了相同的方法。

这里，删除、插入和替换计数分别为 1、3 和 2。显然，将 **A** 转换为 **V** 需要向 $S_{1}$ 插入 3 个字符 **（ # ）**、**A**、**D**。同样，为了将前缀 **A** 替换为 **V**，需要从 $S_{2}$ 删除 2 个字符 **A** 和 **D**。最后，**A** 和 **V** 之间的最小距离计算为 $M[1][3] = min(2,4,3) = 2$。

然后，计算 **A** 前缀与 $S_{2}$ 中后续前缀 **E**、**R**、**B**、**…**、**S** 之间的最小距离，直到最终得到 **A** 和 **S** 前缀的最小距离 $M[1][7] = 6$。

同样，在第 2 行中，基于 M 的第 1 行中先前得到的最小距离，计算 $S_{1}$ 中后续前缀 **D** 与 $S_{2}$ 中所有相应前缀 **A**、**D**、**V**、**…**、**B**、**S** 之间的距离。

例如，$S_{1}[2]$ = **D** 和 $S_{2}[1]$ = **A** 前缀之间的最小编辑距离 $M[2][1]$ 是 $S_{1}$ 和 $S_{2}$ 的（**A**, **#**）、（**D**, **#**）和（**A**, **A**）前缀之间相应距离的最小值。通常，这需要从 $S_{1}$ 中删除 2 个字符 **#**、**A**，以及仅替换 **A** 为 **D** 1 次，通过将 $S_{1}$ 的第一个字符 **A** 追加到 $S_{2}$ 的末尾，并从 $S_{1}$ 中删除它，如下所示：

在这里，从 $S_{1}$ 中删除的字符数也是前一个第 1 行中（**D**, **#**）前缀之间的最小距离 $M[2][0]$，因为在这两种情况下都必须删除 **#**、**A** 两个字符。同样，替换计数等于（**A**, **#**）之间的最小距离，因为将 **D** 转换为 **A** 依赖于先前将 **A** 转换为 **( # )** 的转换。在这种情况下，替换计数为 $1$，因为只有 1 个字符 **A** 从 $S_{1}$ 中删除并插入到 $S_{2}$ 中，在 $S_{1}$ 和 $S_{2}$ 中分别匹配 **D** 和 **A** 前缀在相同位置。最后，不存在通过向 $S_{1}$ 插入字符将前缀 **D** 转换为 **A** 的情况，也不需要在 $S_{1}$ 中删除或替换字符。因此，此转换的插入计数为 $0$。

因此，前缀 **D** 和 **A** 之间的最小距离为 $M[2][0] = min(3,1,2) = 1$。

相等前缀 $S_{1}[2]$ = **D** 和 $S_{2}[2]$ = **D** 之间的最小距离 $M[2][2]$ 等于 $0$。此距离 $M[2][2] = 0$ 的计算方式与前面讨论的 **A** 和 **A** 前缀的距离类似。

这里，前缀 $S_{1}[2]$ = **D** 和 $S_{2}[3]$ = **V** 之间的最小距离 $M[2][3]$ 是一个特别有趣的点。

通过向 $S_{1}$ 插入字符将 **D** 前缀转换为 **V** 前缀，需要先进行 **A** 到 **V** 的转换，通过将前缀 **A** 替换为 **D** 来实现。将 **A** 替换为 **D** 的操作是通过将字符 **A** 插入 $S_{1}$ 并从 $S_{2}$ 删除来完成的。此处，**A** 和 **D** 前缀的插入计数为 $1$，而 **A** 到 **V** 转换的最小距离 $M[1][1]$ 分别为 $2$。因此，**D** 到 **V** 转换的插入计数等于 **A** 和 **V** 之间的最小距离 $M[1][1]$，即 $2$。

反过来，**D** 到 **V** 转换的替换计数也等于 **A** 和 **D** 前缀之间的最小编辑距离 $M[1][2]$，因为前缀 **A** 无法通过从 $S_{1}$ 中删除字符来转换为 **D**，并且 $S_{1}$ 的前缀 **D** 后面跟着相等的（** # **）和 **A** 前缀，它们匹配 $S_{1}$ 和 $S_{2}$ 中的相同位置。此处，将前缀 **( # )** 转换为 **A**，以及将 **A** 转换为 **( # )** 的插入和删除的计数为 $1$，而相等前缀 **A** 的替换计数为 $0$。显然，前缀 **A** 和 **D** 之间的最小距离为 $M[1][2] = min(2,2,1) = 1$。最后，**D** 到 **V** 转换的替换计数为 $1$。

类似地，**D** 和 **V** 前缀的删除计数是相等前缀 **D** 和 **D** 转换的最小编辑距离 $M[2][2]$，因为不可能通过从 $S_{1}$ 删除字符来将 **D** 转换为 **V**，并且在 $S_{1}$ 和 $S_{2}$ 中，前缀 D 在其位置上都相同。因此，替换计数等于 $0$，这既是 **D** 到 **D** 转换的最小编辑距离，也是 **D** 和 **V** 前缀的删除计数，分别。据此，**D** 和 **V** 前缀之间的最小编辑距离 $M[2][3]$ 被计算为上述编辑计数中的最小值，$M[2][3] = min(1,3,2) = 1$。

上述计算继续进行到矩阵 $M$ 中的所有剩余距离，直到根据所有先前最小距离的观察，最终得到 $S_{1}[6] =$ **R** 和 $S_{2}[7]$ = **S** 前缀之间的最后一个最小距离 $M[6][7]$。最小编辑距离 $M[6][7]$ 是 $S_{1}$ 和 $S_{2}$ 完整字符串的 Levenshtein 距离，其值为 $3$。

最后，Levenshtein 距离可以不计算完整的矩阵 M 来评估，因为 $S_{1}$ 的 $i$-字符前缀与 $S_{2}$ 的所有 $j$-字符前缀之间的最小距离在每个 $i$-行中，仅基于矩阵 $(i-1)$-行中的值获得。其他先前行中的距离值不用于此类计算，因此被简单丢弃。

Levenshtein 距离到相似度得分的转换

对于许多应用程序，$S_{1}$ 和 $S_{2}$ 字符串之间的 Levenshtein 距离必须转换为 $[0;1]$ 区间内的相似度得分值。相似度得分是根据 $S_{1}$ 和 $S_{2}$ 字符串的 Hamming 距离计算的，该距离已归一化到相同的 $[0;1]$ 区间。由于 Hamming 距离 $D_{h}$ 始终是 Levenshtein 距离 $\mathcal{Lev}(S_{1},S_{2})$ 的上限，因此很容易计算 $S_{L}$ 相似度得分，该得分表示 Levenshtein 距离在 $[0;D_{h})$ 区间内，而不是 $[0;1]$。

相似度 $S_{L}$ 值有几个步骤，如下：

1. 计算 $S_{1}$ 和 $S_{2}$ 字符串之间的 Hamming 距离 $D_{h}$。

2. 使用以下公式将距离 $D_{h}$ 归一化到 $[0;1]$ 区间：

$H_{norm} = \frac{D_{h}}{max\{|S_{1}|,|S_{2}|\}}$

3. 计算相似度得分 $S_{L}$，该得分表示 Levenshtein 距离 $\mathcal{Lev}(S_{1},S_{2})$ 在 $[0;D_{h})$ 区间内：

$S_{L} = 1.0 - \frac{\mathcal{Lev}(S_{1},S_{2})\times{H_{norm}}}{D_h}$

在上面的公式中，Levenshtein 距离 $\mathcal{Lev}(S_{1},S_{2})$ 乘以归一化值 $H_{norm}$，除以 Hamming 距离 $D_{h}$，然后从 $1.0$ 中减去。

这里，$S_{1}$ 和 $S_{2}$ 之间的 Levenshtein 距离使用经典的 min-max 归一化公式进行归一化。最后，最大的 Levenshtein 距离 $\mathcal{Lev}(S_{1},S_{2})$ 对应于最小的相似度得分 $S_{L}$，反之亦然。

使用代码

下面列出了一个使用 NumPy 在 Python 3 中实现最优 Wagner-Fischer 算法的函数。`d_lev(s1,s2,c=[],dtype=np.uint32)` 函数计算长度不同（$len(s1) != len(s2)$）的两个字符串 `s1` 和 `s2` 的 Levenshtein 最小编辑距离。当未定义成本数组 c 时，删除、插入和替换的成本都等于 1（例如，`c = [1,1,1]`）。

def d_lev(s1,s2,c=[],dtype=np.uint32):
    
    # Initialize the vector e_d[0..|s2|] with the minimal edit distances |j|, 
    # between s1[0] (i.e., the prefix '#') and each of the s2[j], j=[0..|s2|) prefixes.
    e_d = np.arange(len(s2) + 0, dtype=dtype)

    # If s1 equals to s2, the mininal edit distance is 0
    if s1 == s2: return 0
    # If c is undefined, all edit costs are 1 (default)
    if c is d_lev.__defaults__[0]: 
       c = np.ones(3, dtype)

    # Compute the minimal edit distances for all combinations 
    # of prefixes s1[i] and s2[j] as the minimal of distances between the other prefixes. 
    for i in np.arange(1,len(s1)):

        # Initialize the "insertions" vector e_i[0..|s2|), in which
        # the first element e_i[0] is the prefix length |i| of s1, 
        # and all other elements e_i[1..|s2| + 1] are zeros:
        e_i = np.concatenate(([i], np.zeros(len(s2) - 1, dtype)), axis=0)

        for j in np.arange(1,len(s2) + 0):

            # Get the replacement cost for the prefixes s1[i],s2[j]:
            # The r_cost is 0 if the s1[i] and s2[j] are the same, 
            # and is equal to 1, unless otherwise
            r_cost = 0 if s1[i - 1] == s2[j - 1] else 1
            
            # Evaluate the distance between s1[i] and s2[j] as the minimal of the deletion, 
            # insertion, and replacement counts of the s1[i] into s2[j] transformation
            e_i[j] = np.min([ \
               (e_d[j] + 1) * c[0],           # s1[i] - deleted from s1, and inserted to s2
               (e_i[j - 1] + 1) * c[1],       # s2[j] - inserted to s1, and deleted from s2
               (e_d[j - 1] + r_cost) * c[2]]) # s1[i] - replaced by s2[j]

        # Copy the current "insertions" vector e_i to the "deletions" vector e_d.
        # The e_i and e_d vectors are not necessary to be swapped.
        e_d = np.array(e_i, copy=True)

    # The Levenshtein distance e_d[|e_d|-1] between s1 and s2
    return e_d[len(e_d) - 1]

上面列出的代码使用两个向量（行）`e_d` 和 `e_i`，长度为 `|s2|`，用于存储“删除”和“插入”计数。向量 `e_d` 使用必须插入到空前缀 `s1[0] = #` 以将其转换为 `s2[0..|s2|)` 的每个前缀的绝对计数进行初始化：`e_d=[0, 1, 2, 3,..., |s2|]`。此外，向量 `e_i` 在每次迭代时进行初始化，将其第一个值 `e_i[0]=|i|` 分配给前缀长度 `|i|`，而所有其他值设置为 `e_i[1..|s2|] = 0`。对于 `s1[0..|i|], i=[1..|s1|)` 和 `s2[0..|j|], j=[1..|s2|)` 前缀的每一对，它根据 Levenshtein 距离公式计算“删除”、“插入”或“替换”计数的最小值，该公式应用于 `e_d` 和 `e_i` 向量中先前距离，分别。新值存储在向量 `e_i` 中，`e_d` 向量的值通过将新的 `e_i` 向量复制到 `e_d` 来更新。在计算结束时，`e_d` 向量中的最后一个值是字符串 `s1` 和 `s2` 之间的 Levenshtein 距离。

我还实现了其他距离度量，例如 Sørensen 指数和 Hamming 距离。下面列出的代码片段实现了 Sørensen 指数的计算。

def sorensen_score(s1,s2):
    # The Sorensen's index value is equal to 1 if s1,s2 are equal
    if s1 == s2: return 1.0

    # The unique characters from the arrays s1 and s2
    s1 = np.unique(np.asarray(list(s1)))
    s2 = np.unique(np.asarray(list(s2)))
    
    # Computes the count of characters in the intersection of s1 and s2,
    # divided by the length of the largest string, and multipled by 100%
    return np.multiply(100, \
        np.divide(np.size(np.intersect1d(s1,s2)), \
                  np.max((np.size(s1),np.size(s2)))))</span>

Sørensen 指数的值可以简单地计算为 `s1` 和 `s2` 字符串的交集中相等字符的计数，除以最长字符串的大小。

下面列出的另一代码片段实现了 Hamming 距离度量。

def hamming_dist(s1,s2):
    
    # The distance is 0 if s1,s2 are equal
    if s1 == s2: return 0

    # arrays of characters s1,s2
    s1 = np.asarray(list(s1))
    s2 = np.asarray(list(s2))

    # l_diff - the difference of the s1,s2 lengths
    l_diff = abs(np.size(s1) - np.size(s2))

    # l_min - the smallest of s1,s2 lengths
    l_min = np.min((np.size(s1),np.size(s2)))
    
    # The arrays s1,s2 are justified to the length of a shortest string, s1 or s2.
    # Hamming distance is the count of those characters, are not the same at 
    # their positions in the s1 and s2 arrays
    return np.count_nonzero(s1[:l_min] != s2[:l_min]) + l_diff

为了评估长度不同的字符串 `s1` 和 `s2` 之间的 Hamming 距离，获取 `s1` 和 `s2` 的长度中的较小值 `l_min` 以及它们长度的差值 `l_diff`。然后，将较长的字符串（`s1` 或 `s2`）截断到较短字符串的长度，使得 `s1[:l_min]` 和 `s2[:l_min]`。它应用搜索来获取 `s1` 和 `s2` 的字符不相等的位数。Hamming 距离值计算为此类位置的计数，加上 `l_diff` 值，并从函数返回。

此处还有一些代码片段，用于将 Hamming 和 Levenshtein 距离转换为字符串相似度得分。

Hamming 距离通过将其值归一化到 $[0..1]$ 区间进行转换。下面代码片段演示了这种计算。

def hamm_score(s1,s2,d):
    # The similarity score is 1 if s1,s2 are equal
    if s1 == s2: return 1.0

    # Divide the Hamming distance by the length of the 
    # largest of s1,s2 strings, subtracted from 1.0
    return 1.0 - d / np.max((len(s1),len(s2)))

如果字符串 `s1` 和 `s2` 相同，则结果的相似度得分为 $1.0$。否则，Hamming 距离 `d` 除以 `len(s1)` 和 `len(s2)` 中的较大值，表示 $[0..1]$ 区间内的距离。距离值最小的字符串最相似。这就是为什么将归一化距离值从 $1.0$ 中减去以获得 `s1` 和 `s2` 字符串的正确相似度。

Levenshtein 距离到相似度得分的转换略有不同。Levenshtein 距离的上限是相同的 Hamming 距离值。因此，Levenshtein 距离在 $[0..D_{h}]$ 区间内进行归一化，而不是 $[0..1]$，如下面代码片段所示：

def lev_score(s1,s2,dl):
    # The similarity score is 1 if s1,s2 are equal
    if s1 == s2: return 1.0
    # Compute the Hamming distance of the s1,s2 strings
    dh = hamming_dist(s1,s2)
    # Normalize the Hamming distance in the interval [0,1]
    h_norm = dh / np.max((len(s1),len(s2)))
    # Multiply the Levenshtein distance of s1,s2 by the Hamming similarity score,
    # divided by the Hamming distance, and subtacting it from 1.0
    return 1.0 - dl * h_norm / dh

为了获得相似度得分，会计算 `s1` 和 `s2` 字符串的 Hamming 距离 `dh`。然后，Levenshtein 和 Hamming 距离 `dl` 和 `dh` 都在相同的 $[0..1]$ 区间内进行归一化。Levenshtein 距离值在 $[0..D_{h}]$ 区间内表示，为 Levenshtein `dl` 和归一化 Hamming 距离 `h_norm` 的乘积，除以 Hamming 距离 `dh`，并从 $1.0$ 中减去。

除了最优 Wagner-Fisher 算法的实现外，我还开发了演示 Levenshtein 距离和相似度得分计算的代码，用于处理存储在 `strings.txt` 文件中的各种字符串，并调查 Levenshtein 距离和其他度量的效率。

下面列出了 Python3 和 NumPy 中演示应用程序的代码。

函数 `survey_metrics(s1,s2)` 为两个输入字符串 `s1` 和 `s2` 计算 Hamming 和 Levenshtein 距离以及相应的相似度得分值。

def survey_metrics(s1,s2):
    # Compute all distance metrics for s1 and s2
    dists = { 'dl' : d_lev(s1,s2), 
              'hm' : hamming_dist(s1,s2) }
    # Compute the similarity score for each of the metrics
    score = { 'dl' : lev_score(s1,s2,dists['dl']), 
              'hm' : hamm_score(s1,s2,dists['hm']) } 
    # Return the statistics for all metrics, previously computed
    return np.array([{ 'name': name, 'd': dists[d], 's' : score[s] } \
        for [name,d,s] in zip(mt_names, dists.keys(), score.keys())], dtype=object)

另一个 `survey(s1,s2)` 函数生成 `s1` 和 `s2` 字符串的距离和相似度得分值的格式化输出。

def survey(s1,s2):
    # Compute the metrics and similarity scores for s1 and s2
    output = ""; results = survey_metrics(s1, s2)
    # Check if the Levenshtein metrics for s1 and s2 is valid
    valid = is_dl_valid(s1,s2,results[0]['d'],results[1]['d'])
    # Output strings s1 and s2 and their lengths
    output += "strings      : [ \"%s\" -> \"%s\" ]\n\n" % (s1, s2)
    # Output all metrics distance values for s1 and s2
    output += "distance     : [ " + " | ".join(["%s : %4.2f" % \
           (mt['name'],mt['d']) for mt in results]) + " ]\n"
    # Output all metrics similarity scores for s1 and s2
    output += "similarity   : [ " + " | ".join(["%s : %4.2f%%" % \
           (mt['name'],np.multiply(100, mt['s'])) for mt in results])
    # Output the Sorensen's score for s1 and s2
    output += " | Sorensen's Score: %4.2f%%" % sorensen_score(s1,s2) + " ]\n"
    # Output the verification status s1 and s2
    output += "verification : [ %s ]\n\n" % valid

    return output

最后，`demo(filename)` 函数从 `strings.txt` 文件加载字符串数组，并对数组中的每对相邻字符串执行计算，提供距离和相似度得分的输出。

def demo(filename):

    # Output the full path of the string file
    output = "Filename%s: %s\n\n" % \
        (" " * 5, os.path.abspath(filename));

    # Read all string from file 'strings.txt'
    with open(filename,'r') as f:
         strings = f.read().split('\n')
         # For each pair of strings compute the similarity score,
         # based on Levenshtein distance and other metrics
         for i in np.arange(len(strings)-1):
             if len(strings[i]) > 1 and len(strings[i + 1]) > 1:
                # Compute metrics of strings[i] and strings[i + 1], and output the survey
                print(survey(strings[i],strings[i + 1])); time.sleep(1)

    return output

mt_names = ["Levenshtein Distance", "Hamming Distance"]
app_logo = "Levenshtein Distance-Based Similarity Score 0.1a | " + \
           "Arthur V. Ratz @ CodeProject 2022"

if __name__ == "__main__":
    print(app_logo + "\n" + "=" * len(app_logo) + "\n\n")
    print(demo("strings.txt"))

关注点

本文讨论的 Wagner-Fischer 算法能够有效地评估文本数据的 Levenshtein 距离和相似度。该算法计算两个字符串之间的距离，该距离已经是 Damerau-Levenshtein 距离，能够识别相邻字符的转置。最后，Wagner-Fischer 算法易于在大多数编程语言中实现，不仅包括 Haskell 或 Python，还包括 C++、Java、Node.js 等。

参考文献

历史

2022 年 9 月 17 日 - 文章已发布。

\(M[i-1][j] + 1\)	从 S₁ 删除，插入到 S₂
\(M[i][j-1] + 1\)	插入到 S₁，从 S₂ 删除
\(M[i-1][j-1] + 1_{(S_{1}[i]\neq{S_{2}[j]})}\)	替换 S₁[i] 为 S₂[j]