具有收敛加速的级数求和
5.00/5 (4投票s)
如何加速数学级数的收敛
引言
许多应用程序实现了某种级数或序列的计算,这些级数或序列的收敛速度可能非常慢,或者可能需要比暴力实现更高的精度。在实现这些加速技术时有几种选择,我将在本文中介绍最常见的一些。
然而,存在一个问题,即您无法找到一种适用于所有序列的通用加速技术,这已被数学证明。如果您有兴趣自己查找,这个证明是基于序列的一种称为残余的性质。这给您的提示是,在向客户发布之前,要么进行数学测试/证明,要么至少自行判断先在级数上测试加速技术。并且您不应该期望同样的“魔法”能普遍适用。
背景
假设我们有一个序列或级数,其实际(理论)和为 \(S\),但我们只能计算近似值 \(S_n\)。
这个分析也可以用于无穷积
所以,以最通用的方式描述手头的问题,我们只是想最小化差值 \(S - S_n = e\),如果可能的话,消除误差 \(e\)。估计误差函数的形状并利用这些信息创建校正称为核,实际上这是我们所知的使这些算法更快收敛或更精确的唯一方法。如果我们知道每次迭代过程后误差是如何增长的,我们实际上可以利用这些知识来预测比暴力计算更好的真实值。此外,由于我们必须猜测超出我们目前所知的值,因此我们将所有这些带有核校正误差的实现称为数学中的外推法。
艾特肯求和公式
我们进行求和的许多级数本质上是几何增长的,所以一开始很自然地假设误差和校正核可以用公式 \(b \cdot q^n\) 来描述。我们想要用来尝试校正和调整完整和的核是
我们这里假设 \(q < 1\),这样原始级数中我们求和的每个迭代项的误差实际上都会减小。有了上面的通用核,方程中有 3 个未知数 \(S, b, q\) 需要求解,这意味着我们需要 3 个方程才能得到唯一解。结果就是著名的艾特肯公式
这个公式的第一个发现者似乎是日本数学家关孝和,大约在 1680 年。(由于日文拼写的一些相似之处,他有时被误称为 Seki Kowa)。在将这种加速序列的方法命名为 Aitken 之前,也有其他人独立发现过它。
代码实现起来非常直接
/// <summary>
/// Calculates the Aitken summation
/// </summary>
/// <param name="S_n">The partial sums of a series</param>
/// <returns>A extrapolated value for the partial sum</returns>
/// <exception cref="Exception">If you have less than 3 items,
/// this will return with an exception</exception>
public double Aitken(double[] S_n)
{
if (S_n.Length > 3)
{
double S_2 = S_n[S_n.Length - 1];
double S_1 = S_n[S_n.Length - 2];
double S_0 = S_n[S_n.Length - 3];
return (S_2 * S_0 - S_1 * S_1) / (S_2 -2*S_1 + S_0);
}
else
throw new Exception("Must have at least 3 partial sums
to give the correct value");
}
艾特肯公式确实可以加速所有线性收敛级数,此外,它还可以用于加速更困难的对数序列。这个算法也可以在多个阶段使用,这意味着我们对同一个求和级数反复应用它。
Shanks 变换和 Wynn 的 Epsilon 算法
几何级数的通用加速核后来被Shanks 变换公式化,其中 Shanks 用更多的变量公式化了修正项
这将导致 2m + 1 个未知数,Shanks 于 1947 年发现了通用行列式比率
矩阵中的大多数元素由连续项的许多有限差分项组成,因此这些元素通常缩写为 \( \Delta S_p = S_{p+1} - S_p \)。矩阵前面和后面的绝对标记表示您应该计算它的行列式,尽管可以通过创建下(或上)三角矩阵并简单地乘以结果对角线元素来找到行列式,但它通常不是一个稳定的方法。这里的问题是,这种形式的矩阵的 Henkel 行列式使用多个算术运算,当直接在计算机上实现时,可能导致显著的截断误差。因此,使用不同的方法是可取的。
由于一个序列的完整 Shanks 变换等同于 Pade 近似,因此它背后还有一个更隐秘的模式。实际上,可以利用 Shanks 变换来计算完整的 Pade 近似,这也是由于与连分数的关系而找到收敛级数的最快方法。但同样的计算问题依然存在,我们需要一种更好的方法来计算这种变换。
Peter Wynn 的 \(\epsilon\)-算法通过迭代过程产生相同的结果,事实上,它与计算级数的连分数非常相似。我们首先假设我们有一个用 X,Y 表示的表格,其中我们定义左上角为 0,0。在第一列中,我们用零填充它 \(\epsilon(0,y) = 0\),在第二列中,我们放置每次迭代的偏和 \(\epsilon(1,y) = S_n\)。我们现在使用下面的迭代方案
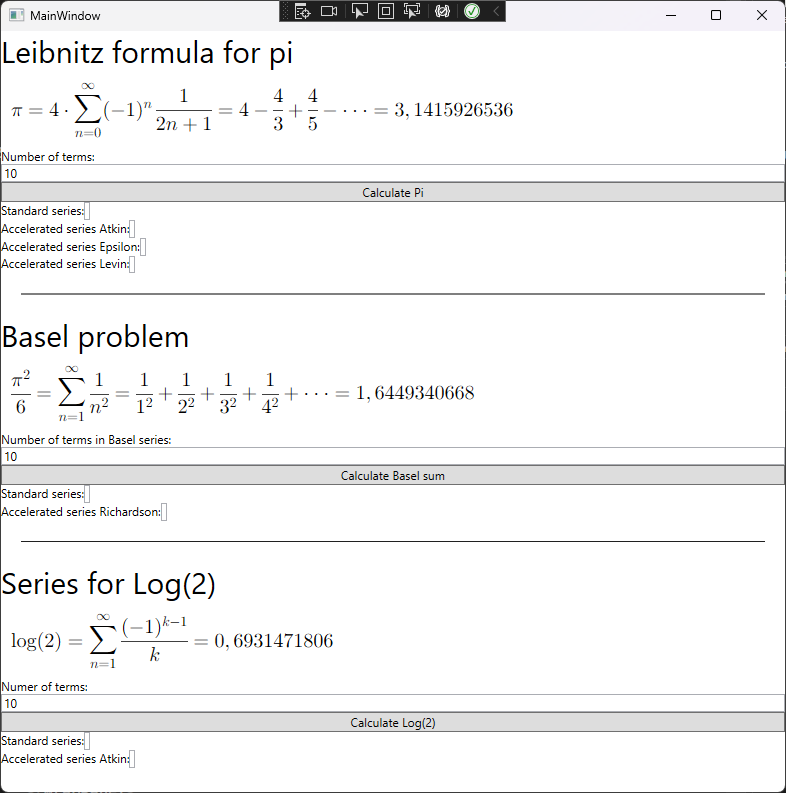
收敛加速用于 \(\pi\) 的缓慢收敛的莱布尼茨公式,并可以用下图中的表格来说明

一种更好,或者至少更常见的说明这种关系的方法是使用菱形图(图片取自 https://www.sciencedirect.com/science/article/pii/S0377042700003551#FIG1)。原因是菱形图中在每个迭代步骤中使用的所有值都彼此相邻。

从计算中可以看出,每个偶数列只包含一些用于计算更高阶变换的中间结果。这些中间结果可以通过 Wynn 交叉规则跳过,该规则允许您只存储奇数列。这里的问题是,您需要 3 个起始列以及参数 \( \epsilon_{-2}^{(n)} = \infty \)、\( \epsilon_{-1}^{(n)} = 0 \) 和最后的 \( \epsilon_{0}^{(n)} = S_n \) 来实现下面的迭代过程:
在计算机上实现这个算法并没有真正的优势,除了它消除了包含中间计算结果的列,但它的缺点是需要一个额外的起始条件。更值得一提的是,Wynn 还发现了一个只用一个向量和两个中间变量就可以计算加速和的实现。但在现代计算机上这不是问题,我将跳过这个推导。您可能已经猜到了,Peter Wynn 的 \(\epsilon\)-算法也可以用于计算 Hankel 行列式、Pade 近似,并且令人惊讶地也可以用于求解称为 Korteweg–De Vries (KdV) 方程的微分波型方程。
现在我们转到代码的实际实现,首先,我们需要加速算法要加速的测试级数。我们之前已经通过莱布尼茨发现的用于 pi 的缓慢收敛级数说明了算法的有用性,该级数由以下公式给出
截断级数中每个新项的求和结果都保存在一个列表中并返回。
public static double[] PartialSumPi_Leibnitz(int n = 6)
{
double sum = 0;
double sign = 1;
double[] result = new double[n];
int ind = 0;
for (int i = 1; i < n*2; i= i+2)
{
sum = sum + sign * 4 / i;
sign *= -1;
result[ind] = sum;
ind += 1;
}
return result;
}
Wynn 算法的实际代码如下所示
/// <summary>
/// Peter Wynns epsilon algorithm for calculating accelerated convergence
/// </summary>
/// <param name="S_n">The partial sums</param>
/// <returns>The best accelerated sum it finds</returns>
public static double EpsilonAlgorithm(double[] S_n, bool Logaritmic = false)
{
int m = S_n.Length;
double[,] r = new double[m + 1, m + 1];
// Fill in the partial sums in the 1 column
for (int i = 0; i < m; i++)
r[i, 1] = S_n[i];
// Epsilon algorithm
for (int column = 2; column <= m; column++)
{
for (int row = 0; row < m - column + 1; row++)
{
//Check for divisions of zero (other checks should be done here)
double divisor = (r[row + 1, column - 1] - r[row, column - 1]);
// Epsilon
double numerator = 1;
if (Logaritmic)
numerator = column + 1;
if (divisor != 0)
r[row, column] = r[row + 1, column - 2] + numerator / divisor;
else
r[row, column] = 0;
}
}
// Clean up, only interested in the odd number columns
int items = (int)System.Math.Floor((double)((m + 1) / 2));
double[,] e = new double[m, items];
for (int row = 0; row < m; row++)
{
int index = 0;
for (int column = 1; column < m + 1; column = column + 2)
{
if (row + index == m)
break;
//e[row + index, index] = r[row, column];
e[row, index] = r[row, column];
index += 1;
}
}
return e[0, e.GetLength(1) - 1];
}
还提出了其他基于 \(\epsilon\)-算法的算法,例如 Wynn 的 \(\rho\)-算法
这里 \( x_n \) 是序列中使用的插值点。在通常的整数和的情况下,使用简化式 \( x_n = n + 1\)。
这些算法通常更适用于加速具有对数增长误差的级数。
Richardson 外推法和欧拉交错级数变换
两种相似的加速收敛方法通常不归为一类,尽管 Richardson 外推法通过泰勒展开计算,而欧拉变换则通过其发明者欧拉一个巧妙的技巧进行有限差分近似。我们从已知的未知函数 \( f(x) \) 的泰勒展开开始,其中函数通过少量 \( h \) 进行调整。顺便说一句,泰勒展开是每个数学家在应用数学中最喜欢的方法。没有一天不用它。嗯,几乎没有,所以万一您忘了,它在这里
在 Richardson 外推法中,我们利用泰勒级数的结构,其中 \( h \) 有不同的倍数值,如 \( 2h, 3h, \cdots \)。这些信息通过一个方程组被利用,使我们能够消除泰勒展开中越来越高阶的导数。在广义 Richardson 外推法中,我们采用泰勒展开的思想,并使用整数和,将 \( \frac{1}{n} \) 的值代替 \( h \),并用误差估计重新公式化和
由此产生的封闭形式解方程,将给我们一个唯一的解,如下面的方程所示。(推导和结果取自 Bender 和 Orszag 的《科学家和工程师的高级数学方法》)
求解 \(S\) 给出 m 个方程的解
Richardson 外推法的代码的弱点在于对阶乘的依赖,有效地限制了计算机上更高阶的实现
/// <summary>
/// Generalized Richardson extrapolation
/// </summary>
/// <param name="S_n">The partial sums</param>
/// <returns>Best approximation of S</returns>
public static double RichardsonExtrapolation(double[] S_n)
{
double S = 0d;
double m = S_n.Length;
for (int j = 1; j <= (int)m; j++)
{
S += System.Math.Pow(-1, m + (double)j) *
S_n[j - 1] *
System.Math.Pow((double)j, m - 1)
/ (Factorial(j - 1) * Factorial(m - j));
}
return S;
}
接下来要展示的是欧拉级数变换,它通常应用于以下形式的交错级数
上述级数的欧拉变换如下所示
这里通用差分公式定义为
这里实际上发生的事情,以及欧拉的卓越洞察力,是交错级数可以写成
顺便说一句,您总是可以指望欧拉令人惊讶地简单而聪明。如果一个问题有简单的解决方案,他通常能找到它。对交错级数多次进行变换实际上意味着我们使用越来越高阶的有限差分,并且每次都得到越来越好的近似。
实际上,泰勒公式与有限差分等价式之间的区别可以通过微积分中的指数数 \( e \) 和差分等价式 2 来表示
幂次 \(X^{\underline{2}}\) 中的下划线称为下降幂
这个公式相当通用,你甚至可以代入有理数,比如 \( 2^{\frac{1}{2}} = \sqrt{2}\),公式仍然有效。这是牛顿对二项式系数的巨大洞察力,使他能够计算数字的平方根。
现在是执行欧拉变换的代码,如下所示
/// <summary>
/// Euler transform that transforms the alternating series
/// a_0 into a faster convergence with no negative coefficients
/// </summary>
/// <param name="a_0">The alternating power series</param>
/// <returns></returns>
public static double[] EulerTransformation(double[] a_0)
{
// Each series item
List<double> a_k = new List<double>();
// finite difference of each item
double delta_a_0 = 0;
for (int k = 0; k < a_0.Length; k++)
{
delta_a_0 = 0;
for (int m = 0; m <= k; m++)
{
double choose_k_over_m = (double)GetBinCoeff(k, m);
delta_a_0 += System.Math.Pow(-1d, (double)m) *
choose_k_over_m * System.Math.Abs(a_0[(int)(m)]);
}
a_k.Add(System.Math.Pow(1d / 2d, (double)(k + 1)) * delta_a_0);
}
return a_k.ToArray();
}
在一些转换算法的帮助下,也可以将欧拉级数变换应用于非交错级数
其中修改后的级数是以下变换
Levin 变换
Levin 变换基于以下假设:选择 b 大于零,并且适当选择剩余估计 \( \omega_m \) 用于要加速的级数
结果公式如下所示
Levin 算法的代码实现
/// <summary>
/// Levins algorithm L_{k}^{n}(S_n) but k + n has to be less than
/// the length of S_n minus one
/// </summary>
/// <param name="S_n">The partial truncated sums</param>
/// <param name="k">The 'order' of Levins algorithm</param>
/// <param name="n">The n'th point approximation</param>
/// <returns>The accelerated value</returns>
public static double LevinsAlgorithm(double[] S_n, double k = 4, double n = 5)
{
double numerator = 0;
double denominator = 0;
if (k + n > S_n.Length - 1)
throw new ArgumentException("Not enough elements to
sum over with the n'th element with order k");
for (int j = 0; j < n ; j++)
{
double rest = System.Math.Pow(-1d, j) *
GetBinCoeff((double)k, (double)j);
double C_jkn_U = System.Math.Pow((double)(n + j + 1), k - 1);
double C_jkn_L = System.Math.Pow((double)(n + k + 1), k - 1);
double C_njk = C_jkn_U / C_jkn_L;
double S_nj = S_n[(int)n + (int)j];
// t transform that calculates a_n
double g_n = S_n[(int)n + j] - S_n[(int)n + j - 1];
// u transform that calculates (n+k) * a_n
// g_n = (n + k)* (S_n[(int)n + j] - S_n[(int)n + j - 1]);
numerator += rest * C_njk * S_nj / g_n;
denominator += rest * C_njk / g_n;
}
return numerator / denominator;
}
参考文献
书籍
其他在线资源
历史
- 2023年2月9日:初始版本
