动态规划或如何利用之前的计算经验

动态规划简介

动态规划（Dynamic Programming）这个术语最早由著名的美国数学家、计算机技术领域的领先专家理查德·贝尔曼（Richard Bellman）于20世纪50年代提出。动态规划（DP）是一种通过将复杂任务分解为更小的子问题来解决复杂任务的方法。

DP 可以解决的问题必须满足两个标准

1. 最优子结构。在动态规划中意味着，较小子问题的解决方案可以用于解决初始问题。最优子结构是“分治”范式的主要特征。

一个经典的实现例子是归并排序算法，其中我们将问题递归地分解为最简单的子问题（大小为 1 的数组），然后根据每个子问题进行计算。结果用于解决下一层（较大的子问题），直到达到初始层。

2. 重叠子问题。在计算机科学中，如果一个问题可以分解为被多次重用的子问题，则称该问题具有重叠子问题。换句话说，使用相同的输入数据和相同的结果运行相同的代码。这类问题的一个经典例子是计算斐波那契数列中的第 N 个元素，我们将在下面进行探讨。

可以说，DP 是使用分治范式的一种特殊情况，或者是它的一个更复杂的版本。该模式非常适合解决涉及组合学的问题，在这些问题中计算了大量的不同组合，但 N 个元素的数量经常是单调且相同的。

在最优子结构和重叠子问题中，如果我们采用暴力方法，会有大量的重复计算和操作。DP 通过使用两种主要方法：记忆化和制表法，帮助我们优化解决方案并避免重复计算

1. 记忆化（自上而下方法）通过递归实现。一个任务被分解为更小的子问题，其结果被存储在内存中，并通过重复使用组合起来解决原始问题。

• 缺点：这种方法通过递归方法调用使用栈内存。
• 优点：对 DP 任务的灵活性。

2. 制表法（自下而上方法）使用迭代方法实现。子问题从最小到初始按顺序迭代计算。

• 缺点：应用范围有限。这种方法需要对整个子问题序列有初步了解。但在某些问题中，这并不可行。
• 优点：高效的内存使用，因为所有都在单个函数内运行。

理论听起来可能枯燥难懂 — 让我们看一些例子。

问题：斐波那契数列

DP 的一个经典例子是计算斐波那契数列中的第 N 个元素，其中每个元素是前两个元素的和，第一个和第二个元素分别为 0 和 1。

根据假设，我们最初关注最优子结构的性质，因为为了计算一个值，我们需要找到前一个值。为了计算前一个值，我们需要找到它之前的值，依此类推。重叠子任务的性质如下图所示。

对于此任务，我们将探讨三种情况

1. 直接方法：缺点是什么？
2. 使用记忆化的优化解决方案
3. 使用制表法的优化解决方案

直接/暴力方法

你可能想到的第一件事是进入递归，将前两个元素相加，并给出它们的结果。

/**
 * Straightforward(Brute force) approach
 */
fun fibBruteForce(n: Int): Int {
    return when (n) {
        1 -> 0
        2 -> 1
        else -> fibBruteForce(n - 1) + fibBruteForce(n - 2)
    }
}

在下面的屏幕上，你可以看到一个函数调用栈，用于计算序列中的第五个元素。

请注意，函数 fib(1) 被调用了五次，而 fib(2) 被调用了三次。具有相同签名和相同参数的函数被重复启动，并执行相同的操作。当 N 增加时，树的增长不是线性的，而是指数级的，这导致了计算的巨大重复。

数学分析：
时间复杂度：O(2ⁿ)，
空间复杂度：O(n) -> 与递归树的最大深度成正比，因为这是隐式函数调用栈中可能存在的最大元素数量。

结果：这种方法效率极低。例如，计算第 30 个元素需要 1,073,741,824 次操作。

记忆化（自上而下方法）

在这种方法中，实现与前面提到的“暴力”解决方案并没有太大不同，除了内存分配。我们使用变量 memo，在其中收集栈中任何已完成的 fib() 函数的计算结果。

需要注意的是，有一个整数数组并按索引引用它就足够了，但为了概念清晰，创建了一个哈希映射。

/**
 * Memoization(Top-down) approach
 */
val memo = HashMap<Int, Int>().apply {
    this[1] = 0
    this[2] = 1
}

fun fibMemo(n: Int): Int {
    if (!memo.containsKey(n)) {
        val result = fibMemo(n - 1) + fibMemo(n - 2)
        memo[n] = result
    }
    return memo[n]!!
}

让我们再次关注函数调用栈

• 第一个将结果写入 memo 的已完成函数是高亮的 fib(2)。它将控制权返回给高亮的 fib(3)。
• 高亮的 fib(3) 在求和 fib(2) 和 fib(1) 的调用结果后找到其值，将其解决方案输入 memo 并将控制权返回给 fib(4)。
• 我们已经达到了重用先前经验的阶段 — 当控制权返回给 fib(4) 时，fib(2) 调用等待它的轮次。fib(2) 反过来，不是调用 (fib(1) + fib(0))，而是直接使用 memo 中的所有已完成解决方案，并立即返回它。
• fib(4) 被计算并返回控制权给 fib(5)，后者只需启动 fib(3)。在最后的类比中，fib(3) 立即从 memo 返回一个值，无需计算。

我们可以观察到函数调用和计算次数的减少。此外，当 N 增加时，减少的幅度将呈指数级增长。

数学分析
时间复杂度：O(n)
空间复杂度：O(n)

结果：渐近复杂度有明显的差异。与原始解决方案相比，这种方法在时间上将其减少到线性，并且没有增加内存使用。

制表法（自下而上方法）

如上所述，这种方法涉及从较小到较大的子问题的迭代计算。在斐波那契数列的情况下，最小的“子问题”是序列中的第一个和第二个元素，分别为 0 和 1。

我们很清楚这些元素之间的关系，用公式表示：fib(n) = fib(n-1) + fib(n-2)。因为我们知道前面的元素，我们可以很容易地计算出下一个元素，再下一个，依此类推。

通过将我们已知的值相加，我们可以找到下一个元素。我们循环执行此操作，直到找到所需的值。

/**
 * Tabulation(Bottom-up) approach
 */
fun fibTab(n: Int): Int {
    var element = 0
    var nextElement = 1
    for (i in 2 until n) {
        val newNext = element + nextElement
        element = nextElement
        nextElement = newNext
    }
    return nextElement
}

数学分析
时间复杂度：O(n)
空间复杂度：O(1)

结果：这种方法在速度方面与记忆化一样有效，但它使用了恒定的内存量。

问题：唯一二叉树

让我们看一个更复杂的问题：我们需要找到可以用 N 个节点创建的所有结构唯一的二叉树的数量。

二叉树是一种分层数据结构，其中每个节点最多有两个后代。通常，第一个被称为父节点，有两个子节点——左子节点和右子节点。

假设我们需要找到 N = 3 的解决方案。三个节点有 5 棵结构唯一的树。我们可以心算出来，但如果 N 增加，变体会急剧增加，在脑海中可视化这些将是不可能的。

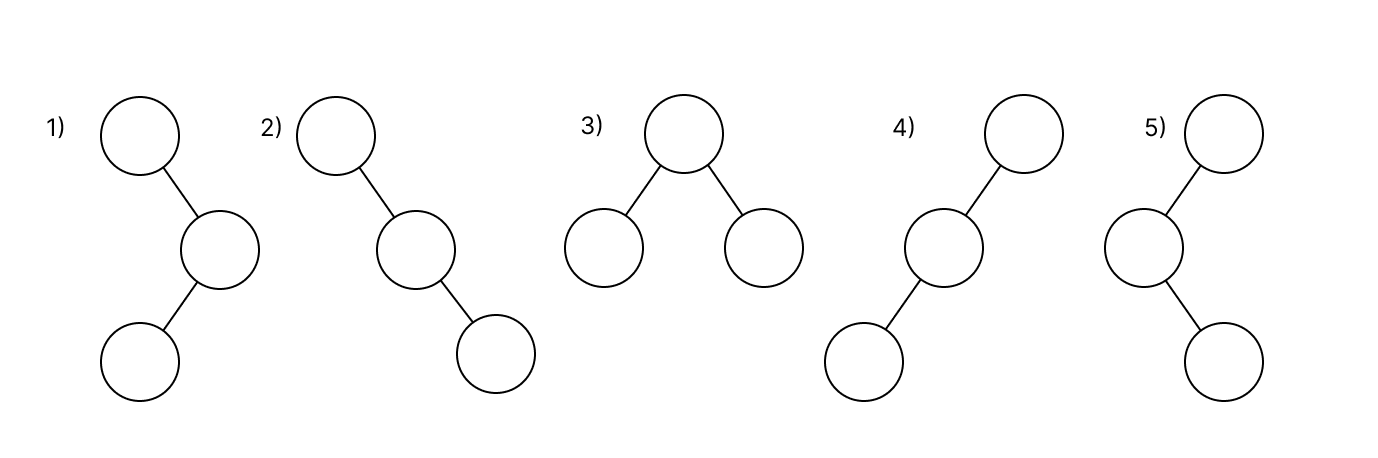
这个任务可以归结为组合学。让我们找出可以形成哪些组合，以及如何找到它们的形成模式。

1. 每棵树都从顶部节点（树的顶点）开始。然后树在深度上扩展。
2. 每个节点都是一个新子树（子树）的开始，如屏幕所示。左子树是绿色的，右子树是红色的。每个子树都有自己的顶点。

让我们以 N = 6 的任务为例，从概念层面进行探讨。我们将我们的计算函数命名为 numOfUniqueTrees(n: Int)。

在我们的示例中，给定 6 个节点，其中一个，根据前面提到的原则，形成树的顶点，其余 5 个形成剩余部分。

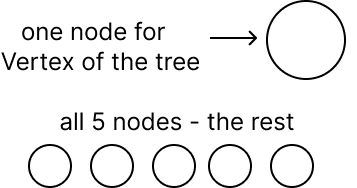
从现在开始，我们与剩余节点进行交互。这可以通过各种方式完成。例如，使用所有五个节点形成左子树，或者将所有五个节点发送到右子树。或者将节点分为两个——2 个到左边，3 个到右边（见下图），我们有有限数量的此类变体。

 

为了获得结果 numOfUniqueTrees(6)，我们需要考虑所有节点分布的变体。它们显示在表格中

表格显示了 6 种不同的节点分布。如果我们找到每种分布可以生成多少唯一树并将它们相加，我们将得到最终结果。

如何找到分布的唯一树的数量？
我们有两个参数：左节点和右节点（表格中的左列和右列）。

结果将等于：numOfUniqueTrees(leftNodes) * numOfUniqueTrees(rightNodes)。

为什么？在左侧，我们将有 X 棵唯一树，对于每棵树，我们可以在右侧放置 Y 种唯一的树变体。我们将它们相乘得到结果。

因此，让我们找出第一种分布（5 左，0 右）的变体。

numOfUniqueTrees(5) * numOfUniqueTrees(0)，因为右侧没有节点。结果是 numOfUniqueTrees(5) — 左侧唯一子树的数量，右侧保持不变。

计算 numOfUniqueTrees(5)。
现在我们有了最小的子问题。我们将像处理较大的问题一样处理它。在这个阶段，DP 任务的特征很清楚——最优子结构，递归行为。

一个节点（绿色节点）被发送到顶点。我们以类似于先前经验的方式（4:0），（3:1），（2:2），（1:3），（0:4）分布剩余的（四个）节点。

我们计算第一个分布（4:0）。它等于 numOfUniqueTrees(4) * numOfUniqueTrees(0) -> numOfUniqueTrees(4) 根据前面的类比。

计算 numOfUniqueTrees(4)。如果我们将一个节点分配给顶点，我们还剩下 3 个。

分布（3:0）、（2:1）、（1:2）、（0:3）。

对于 2 个节点，只有两棵唯一的二叉树，对于 1 个节点，只有一棵。前面我们已经提到，对于三个节点，有 5 种唯一的二叉树变体。

结果——分布（3:0）、（0:3）等于 5，（2:1）、（1:2）等于 2。
如果我们将 5 + 2 + 2 + 5 相加，我们得到 14。numOfUniqueTrees(4) = 14。

根据记忆化的经验，我们将计算结果输入变量 memo。每当我们发现需要找到四个节点的变体时，我们不会再次计算它们，而是重用以前的经验。

让我们回到计算 (5:0)，它等于分布 (4:0)、(3:1)、(2:2)、(1:3)、(0:4) 的总和。我们知道 (4:0) = 14。让我们看看 memo，(3:1) = 5，(2:2) = 4 (左侧 2 个变体 * 右侧 2 个变体)，(1:3) = 5，(0:4) = 14。如果我们将它们相加，我们得到 42，numOfUniqueTrees(5) = 42。

让我们回到 numOfUniqueTrees(6) 的计算，它等于分布的总和

(5:0) = 42, (4:1) = 14, (3:2) = 10 (左侧 5 个 * 右侧 2 个), (2:3) = 10, (1:4) = 14, (0:5) = 42。如果我们将它们相加，我们得到 132，numOfUniqueTrees(5) = 132。

任务解决了！

结果：让我们注意在 N = 6 的解决方案中重叠的子问题。在直接解决方案中，numOfUniqueTrees(3) 将被调用 18 次（下图）。随着 N 的增加，相同计算的重复次数将远大于此。

我强调，（左侧 5 个，右侧 0 个）和（左侧 0 个，右侧 5 个）的唯一树的数量将是相同的。只是在一种情况下它们在左侧，在另一种情况下在右侧。这同样适用于（左侧 4 个，右侧 1 个）和（左侧 1 个，右侧 4 个）。

记忆化作为动态规划的一种方法，使我们能够优化解决这种复杂任务的方案。

实现

class Solution {
    fun numTrees(n: Int): Int {
        val memo = arrayOfNulls<Int>(n+1)
        return calculateTees(n, memo)
    }

    fun calculateTees(n: Int, memo:Array<Int?>): Int {
        var treesNum = 0
        if(n < 1) return 0
        if(n == 2) return 2
        if(n == 1) return 1
        if(memo[n]!=null)
            return memo[n]!!

        for (i in 1..n){
            val leftSubTrees = calculateTees( i - 1, memo)
            val rightSubTrees = calculateTees(n - i, memo)

            treesNum += if(leftSubTrees>0 && rightSubTrees>0){
                leftSubTrees*rightSubTrees
            } else
                leftSubTrees+leftSubTrees
        }
        memo[n] = treesNum
        return treesNum
    }
}

结论

在某些情况下，通过动态规划解决任务可以节省大量时间，并使算法以最高效率运行。

感谢您阅读本文。我很高兴回答您的问题。

历史

• 2023 年 2 月 7 日：初始版本