快速稳定的多项式求根器 - 第五部分
5.00/5 (5投票s)
Durand-Kerner 方法用于多项式求根。一种快速可靠的联立方法
目录
- 引言
- Durand-Kerner 背景
- Durand-Kerner 方法
- Durand-Kerner 方法中多重根的问题
- 安全收敛区域
- 牛顿法与 Durand-Kerner 方法的比较
- 修改什么?
- Durand-Kerner 算法的实现
- C++ 代码
- 其他不使用导数的类 Weierstrass 联立方法
- Aberth-Erhlich 联立方法
- 建议
- 结论
- 参考文献
- 历史
引言
在本文(第五部分)中,我们探讨多项式求根器的联立方法。有两种方法浮现在脑海中。第一种是 Weierstrass 方法,该方法于 1891 年开发,后来在 20 世纪 60 年代被 Durand 和 Kerner 重新发现。另一种方法是 Aberth-Erhlich 方法,也来自 20 世纪 60 年代。有时,第一种方法仅称为 Weierstrass、Durand-Kerner 或有时组合并缩写为 WDK 方法。在本文中,我们将将其称为 Durand-Kerner 方法。
这两种方法都被认为非常稳健和稳定。Durand-Kerner 方法是一种用于同时查找给定多项式所有根的数值技术。该方法因其效率和处理高次多项式能力而在数值分析和计算数学中尤为重要。
Durand-Kerner 背景
该方法由两位数学家 Eugene Durand 和 Arthur Kerner 独立开发。它改进了 Karl Weierstrass 的早期思想,因此其别名为 Weierstrass 方法。Durand-Kerner 方法是一种求根算法,属于联立迭代方法类别,不同于牛顿法等更传统的顺序方法。
多项式问题
给定一个具有实系数或复系数的 n 次多项式,挑战在于找到它的所有根,这些根也可能是复数。这个问题在科学和工程的各个领域都至关重要,因为确定多项式的根是一项频繁的需求。
方法概述
Durand-Kerner 方法从每个根的初始猜测开始。这些猜测最好是不同的。然后,该方法使用特定的公式迭代地细化这些猜测。该方法的美妙之处在于每次迭代中同时更新所有根的近似值,利用多项式在多个点处的行为。
优点
- 效率:该方法对于高次多项式可能非常高效。
- 通用性:它适用于实数多项式和复数多项式。
- 同步收敛:所有根并行细化,从而可能更快地实现整体收敛。
避免典型的降次过程,例如牛顿法
考虑因素
虽然 Durand-Kerner 方法功能强大,但其性能在很大程度上取决于初始猜测。选择不当可能导致收敛缓慢,甚至有时会收敛到错误的值。此外,该方法可能计算量很大,特别是对于根数很多的多项式。
应用
Durand-Kerner 方法在控制理论、信号处理和计算物理等领域都有应用,在这些领域中,求解多项式方程是一项基本任务。
Durand-Kerner 方法作为解决多项式求根古老问题的优雅而高效的解决方案,体现了数学创造力与计算实用性的独特结合。
Durand-Kerner 方法
Durand-Kerner 方法是一种使用以下迭代同时收敛到多项式所有根的方法:

其中 xk 是根的第 k 个近似值,P(xk) 是多项式在 xk 处的值,而

是 xk 与其他近似值 xj 之间的差的乘积。
该方法也称为 Weierstrass 方法,校正因子

称为 Weierstrass 校正。
在上述 Weierstrass (Durand-Kerner) 方法中,“步长”(或 Wk)对于每次迭代,在更新根时,不像牛顿法中的切线那样具有直接的几何解释。然而,我们可以从在复平面中向根移动的角度来考虑它
Weierstrass 方法中的每个根近似值都是复平面中的一个点。在每次迭代中,该点会更接近实际的根。“步长”本质上是每个根近似值在迭代过程中在复平面中移动的距离。
特定根的步长不仅取决于该点的多项式值,还取决于所有其他当前根近似值的位置。这与牛顿法不同,在牛顿法中,每个根的步长与其他根无关。
与牛顿法中的切线或其与 x 轴的交点没有直接对应的东西。相反,Weierstrass 方法向根的移动是基于所有根更复杂的相互作用。
在几何上,可以将根近似值可视化为复平面中的点,这些点逐渐螺旋或以某种模式向多项式的实际根移动。
虽然 Weierstrass 方法缺乏牛顿法那样的直接几何解释,但它可以被视为复平面中的一个动态过程,其中所有根近似值同时向各自的真实根移动,并受到彼此位置的影响。
Durand-Kerner 方法具有二次收敛率(与牛顿法相同),并且与其他求根方法相比具有一些优势。与牛顿法相比,我们可以从上述公式看出,我们不需要多项式的第一导数。其次,它是一种联立方法,因此我们不必担心除以因子或使用降次技术。以及由此产生的因降次过程不准确而累积的误差。
由于我们通常有一个以上的根,我们可以将上述方程写成更简洁的形式:
或使用 Weierstrass 校正
![]()
像往常一样,当重数 > 1 时,该方法仅具有线性收敛性。下面代码示例中使用的起点是原始的,如下所示:
![]()
取多项式
P(x)=(x-1)(x-2)(x-3)(x-4)=1x4-10x3+35x2-50x+24

我们看到收敛率接近略高于 2,符合 Durand-Kerner 方法的预期。另外,请注意,在开始看到一些牵引力之前大约需要 6 次迭代,并且需要 9 到 10 次迭代才能达到所需的精度。
以及向根的迭代轨迹。

我们注意到第二个根(绿色路径)从复数点 (0.4+i0.9) 开始,然后经过一次较长的“旅行”进入复平面,然后才逐渐趋向于根 x=4。第三个根(红色路径)的情况部分相同,它从 (-0.7+i0.7) 开始,然后朝着错误的方向前进,然后掉头,并导航到根 x=3。这对于 Durand-Kerner 方法来说是非常典型的,即最初它可能会朝着看似疯狂的方向发展,然后“振作起来”并朝着根移动。
Durand-Kerner 方法在处理多重根时存在的问题
Durand-Kerner 方法也受到多重根问题的影响,其中收敛率从二次收敛(收敛幂为 2)下降到线性收敛。
取多项式
P(x)=(x-2)(x-2)(x-3)(x-4)=1x4-11x3+44x2-76x+48。
它在 x=2 处有一个双根。

我们看到,在一些初始波动之后,收敛幂稳定在 1 到 2 之间,导致收敛缓慢。我们需要 23 次迭代才能接受结果。
以及通往根的路径。

我们需要实现一个改进版本,该版本也能处理多重根问题。幸运的是,该领域已经进行了研究,并且有多位作者提出了改进收敛率的建议 [8]。然而,据我所知,大多数建议仅略微提高了收敛率,并且缺乏对多重根问题的高效处理。
安全收敛区域
Durand-Kerner 方法被认为非常稳定,几乎总是可以从任何起点收敛。我说“几乎”,因为已有文献记载,你可以找到一个起点,在该起点上该方法不会收敛,但与牛顿法相比,它将更加稳健和有弹性,无论起点如何几乎总能找到一个根。话虽如此,它不应与牛顿法直接比较,而应与第一部分和第二部分中概述的改进牛顿法进行比较。如果我们比较这些版本,这两种方法的稳定性和弹性没有区别。对于 [12] 中的 Durand-Kerner 方法,他们在以下情况下建立了安全收敛区域:

其中 W(k) 是第 k 次迭代的 Weierstrass 校正,n 是多项式次数,而
![]()
计算是否处于安全收敛区域对于 Durand-Kerner 方法的实现非常有用。这里一个小插曲是,当处理多重根时,上述安全收敛区域的标准永远不会达到。相反,我们使用一个技巧:如果 |P(xk)|<e(1/3),其中 e 是多项式求值的停止准则,那么我们也认为它处于安全收敛区域。
牛顿法与 Durand-Kerner 方法的比较
为了将不同的方法与其他方法进行比较,我们可以使用一个著名的效率指标来查看它与其他基于导数的方法相比如何。
效率指标是 q(1/p),其中 q 是方法的收敛阶数,p 是方法的多项式求值次数。对于牛顿法,p 是 2,因为我们需要在每次迭代中评估 P(z) 和 P’(z),牛顿法具有收敛阶数 q=2,因此我们得到效率指标 = 2(1/2)=1.42
对于 Durand-Kerner 方法,我们在每次迭代中只评估 P(x),我们得到 2(1/1)=2
这比牛顿法要大。
Durand-Kerner 方法的优势在于它同时迭代所有根,并且它还避免了许多其他方法需要除以多项式中的一个或两个根的降次过程。然而,缺点之一是对于具有实系数的多项式,我们无法利用复共轭根,而需要使用联立方法单独找到它们。由于过程中的不准确性,这可能导致复数根不严格为复共轭根。此外,Durand-Kerner 方法通常需要更多的迭代才能开始趋近于根,与牛顿法相比。
修改什么?
与牛顿法(第二部分)相比,幸运的是,我们可以重用牛顿法中已有的代码。评估多项式 P(x) 的 Horner 方法是相同的,当 P(x) 足够低可以接受根时,Adams 测试也是如此。我们可以跳过降次过程,因为 Durand-Kerner 方法不需要它。而且,从技术上讲,我们也可以跳过直接求解二次方程,因为所有根将一次性找到。因此,我们对 Durand-Kerner 方法进行了修改步骤:
Durand-Kerner 步骤包括:
- 寻找一个初始点
- 执行 Durand-Kerner 迭代,包括通过 Horner 方法进行多项式求值
- 检测多重根问题
- 计算最终上限。(Adam 测试)
- 求解二次方程。仅当初始多项式的次数为 2 或更低时。
寻找初始点
在第一部分和第二部分中,我们已经为根搜索建立了一个合适的起始点,因此我们知道根总是位于起始点复平面圆外。然而,我们正在同时迭代所有根,因此我们需要为所有根设置初始起始猜测。不幸的是,没有足够的算法来做到这一点。相反,我们使用一个固定的起点,然后将剩余的起点分布在复平面中的一个外圆周围。使用公式:
xi=(0.4+i0.9)i,对于 i=0,…,n-1
类似的技术也在 [11] 中提出过,结果大致相同。
其他起点,例如 Kalantaris。Kalantaris 有一个计算所有根所在的外圆的公式。建议的起点可以是一个内/外圆,起始半径为 Kalantaris 圆的 2/3。选择这种技术似乎是合理的,但测试表明它并没有显著减少迭代次数。
改进的 Durand-Kerner 方法提高了多重根的处理能力
如前所述,目前还没有直接改进的 Durand-Kerner 方法版本可以有效地处理多重根。相反,我们可以采用一个非常简单的解决方案来解决这个问题。当我们处于安全收敛区域时,我们检查我们是否正在处理一个多重根,如果是,我们只需为正在计算的根应用改进的牛顿步。这意味着我们丢弃该根的 Weierstrass 校正,而是使用牛顿步校正

只要 P(xk+1) 减小。然后将最佳牛顿步(最佳 m)作为根的步长返回。
然而,我们如何检测我们正在处理多重根?一个简单的测试是检查由以下公式给出的收敛阶数 q:

对于简单根的正常收敛,q 约等于 2;然而,当接近多重根时,q 通常介于 1.1 和 1.4 之间,而不是 2,如果我们进一步检查我们是否处于安全收敛区域,那么我们就可以相当准确地检测到多重根的情况。
现在选择性地添加牛顿步校正也增加了评估 P'(x) 的需要,而使用未经修改的 Durand-Kerner 时不需要 P'(x)。然而,如果我们想有效地处理多重根,我们就别无选择,只能在多重根的情况下使用改进的牛顿校正。在多重根示例中,迭代次数从 23 次减少到 12 次,这非常值得为该方法添加此牛顿校正。
联立求根搜索的合适停止准则
在第二部分中,我们已经为具有实系数和实数或复数根的多项式建立了合适的停止准则。
由于我们正在同时迭代所有根,并且这些根可能具有不同的数量级,因此我们不能仅仅为多项式求值中的误差建立一个单一的上限。我们必须为每个根携带单独的停止准则。我们确实可以重复使用第二部分中的 Adam 测试,将其单独应用于每个根。由于在更接近根之前无法计算正确的上限,因此我们最初还使用第一部分和第二部分中的简单上限,并且当更接近根时,我们然后为每个根调用 Adam 测试。接近度由以下条件确定:当根 z 的近似值位于先前建立的安全收敛区域内时。此测试确保我们计算正确的上限并确保根搜索正确终止。
Durand-Kerner 算法的实现
我们使用以下算法来修改 Durand-Kerner 算法。
- 消除所有零根
- 如果多项式次数小于 3,则直接求解并退出
- 建立联立根搜索
- 计算每个 x0, x1, …,xn 的初始起点
- 计算每个根 x0, x1, …,xn 的初始停止准则
- 对于每次迭代 k=1,… 执行
- 对于每个根 x0, x1, …,xn
- 如果根 xi 已标记为已找到,则继续下一个根
- 计算 Weierstrass 校正 W(xi)
- 计算下一个近似值
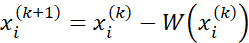
- 计算 xi 的收敛阶数 q
- 如果处于安全收敛区域且 q<1.4
- 执行改进的牛顿多重根收敛步,并用改进的牛顿步更新 W(xi(k))
- 如果处于收敛区域内,则重新计算根 xi 的上限
- if
 或 P(xi(k))<eps 则将根标记为 xi 已完成
或 P(xi(k))<eps 则将根标记为 xi 已完成
- 计算是否已达到安全收敛区域
- 对于每个根 x0, x1, …,xn
- 所有根现已找到
C++ 代码
下面的 C++ 代码使用改进的 Durand-Kerner 方法查找具有实系数的多项式的根。
/*
*******************************************************************************
*
* Copyright (c) 2023
* Henrik Vestermark
* Denmark, USA
*
* All Rights Reserved
*
* This source file is subject to the terms and conditions of
* Henrik Vestermark Software License Agreement which restricts the manner
* in which it may be used.
*
*******************************************************************************
*/
/*
*******************************************************************************
*
* Module name : DurandKerner.cpp
* Module ID Nbr :
* Description : Solve n degree polynomial using the Durand-Kerner method
* --------------------------------------------------------------------------
* Change Record :
*
* Version Author/Date Description of changes
* ------- ------------- ----------------------
* 01.01 HVE/24Nov2023 Initial release
*
* End of Change Record
* --------------------------------------------------------------------------
*/
// define version string
static char _VDURAND_[] =
"@(#)testDurandKerner.cpp 01.01 -- Copyright (C) Henrik Vestermark";
#include <algorithm>
#include <vector>
#include <complex>
#include <limits>
#include <iostream>
#include <functional>
#include <cmath>
using namespace std;
constexpr int MAX_ITER = 200;
// This is the Durand-Kerner method
// It simultaneously finds all the roots
//
static vector<complex<double>> PolynomialRootsDurandKerner
(const vector<double>& coefficients)
{
struct eval { complex<double> z{}; complex<double> pz{}; double apz{}; };
const complex<double> complexzero(0.0); // Complex zero (0+i0)
size_t n=coefficients.size()-1; // Degree of Polynomial p(x)
vector<complex<double>> roots; // Holds the roots of the Polynomial
vector<double> coeff(coefficients.size()); // Holds the current coefficients of P(z)
copy(coefficients.begin(), coefficients.end(), coeff.begin());
// Step 1 eliminate all simple roots
for (; n > 0 && coeff.back() == 0.0; --n)
roots.push_back(complexzero); // Store zero as the root
if (n == 0) // if polynomial empty?
return roots;
// Solve any remaining linear or quadratic polynomial
// For Polynomial with real coefficients a[],
// The complex solutions are stored in the back of the roots
auto quadratic = [&](const std::vector<double>& a)
{
const size_t n = a.size() - 1;
complex<double> v;
double r;
// Notice that a[0] is !=0 since roots=zero has already been handle
if (n == 1)
roots.push_back(complex<double>(-a[1] / a[0], 0));
else
{
if (a[1] == 0.0)
{
r = -a[2] / a[0];
if (r < 0)
{
r = sqrt(-r);
v = complex<double>(0, r);
roots.push_back(v);
roots.push_back(conj(v));
}
else
{
r = sqrt(r);
roots.push_back(complex<double>(r));
roots.push_back(complex<double>(-r));
}
}
else
{
r = 1.0 - 4.0 * a[0] * a[2] / (a[1] * a[1]);
if (r < 0)
{
v = complex<double>(-a[1] /
(2.0 * a[0]), a[1] * sqrt(-r) / (2.0 * a[0]));
roots.push_back(v);
roots.push_back(conj(v));
}
else
{
v = complex<double>((-1.0 - sqrt(r)) * a[1] / (2.0 * a[0]));
roots.push_back(v);
v = complex<double>(a[2] / (a[0] * v.real()));
roots.push_back(v);
}
}
}
return;
};
// Solve it directly?
if (n <= 2)
{
quadratic(coeff);
return roots;
}
// Evaluate a polynomial with real coefficients a[] at a complex point z and
// return the result
// This is Horner's methods avoiding complex arithmetic
auto horner = [](const vector<double>& a, const complex<double> z)
{
const size_t n = a.size() - 1;
double p = -2.0 * z.real();
double q = norm(z);
double s = 0.0;
double r = a[0];
eval e;
for (size_t i = 1; i < n; i++)
{
double t = a[i] - p * r - q * s;
s = r;
r = t;
}
e.z = z;
e.pz = complex<double>(a[n] + z.real() * r - q * s, z.imag() * r);
e.apz = abs(e.pz);
return e;
};
// Calculate an upper bound for the rounding errors performed in a
// polynomial with real coefficient a[] at a complex point z.
// (Adam's test)
auto upperbound = [](const vector<double>& a, const complex<double> z)
{
const size_t n = a.size() - 1;
double p = -2.0 * z.real();
double q = norm(z);
double u = sqrt(q);
double s = 0.0;
double r = a[0];
double e = fabs(r) * (3.5 / 4.5);
double t;
for (size_t i = 1; i < n; i++)
{
t = a[i] - p * r - q * s;
s = r;
r = t;
e = u * e + fabs(t);
}
t = a[n] + z.real() * r - q * s;
e = u * e + fabs(t);
e = (4.5 * e - 3.5 * (fabs(t) + fabs(r) * u) +
fabs(z.real()) * fabs(r)) * 0.5 * pow((double)_DBL_RADIX, -DBL_MANT_DIG + 1);
return e;
};
// Do Durand-Kerner iteration for polynomial order higher than 2,
// The preliminary stopping value for P(x)
const double eps = 4 * n * abs(coeff[n]) * pow((double)_DBL_RADIX, -DBL_MANT_DIG);
const double epsLow = pow(eps, 1.0 / 3.0);
size_t i;
int itercnt; // Hold the number of iterations per root
bool stage1 = true; // Initially stage 1 is set to true when the convergence
// test is true then stage1 is reset to false
complex<double> z; // Use as temporary variable
vector<bool> finish(n, false); // Vector flag indicates if an
// individual root search is finish
vector<double> upper(n, eps); // The individual upper bound for each root
// that needs to be satisfied
vector<complex<double>> W(n); // Weierstrass correction. (step size)
vector<eval> pz; // vector of P(z)
vector<double> coeffprime; // prime coefficients. Only needed when
// multiplicity>1
int found = 0; // No of roots founds
vector<bool> NewtonTry(n, false); // Vector flag indicates if last iteration
// included a Newtonstep (multiplicity>1)
// n>2 do the Durand-Kerner method
// Algorithm only works on polynomials in monic form
for (i = 0; i <= n; ++i)
coeff[i] /= coeff[0];
// Convergence test for the Durand-Kerner method
// Max(W)< MIN(R[i]-R[j])/(2n+1), i=0..n-1, j=0..n-1 and i!=j
auto TestConvergence = [](const vector<complex<double>>& R,
const vector<complex<double>>& W)
{
double wmax = 0.0;
double dmin = numeric_limits<double>::infinity();
const size_t n = W.size(); // W.size() and R.size() are identical
// Compute dmin and wmax
for (size_t i = 0; i < n; i++)
{
wmax = max(wmax, abs(W[i]));
for (size_t j = i+1; j < n; ++j)
dmin = std::min(dmin, abs(R[i] - R[j]));
}
bool isConvergent = (wmax < dmin / (2 * n + 1));
return isConvergent;
};
// Try multiple Newton Steps when dealing with multiple roots
// If there is r multiple roots then the best next step is m=r
auto MultipleNewtonSteps = [&](const vector<double>& a,
const complex<double>& z, const complex<double>& dz)
{eval pzbest = horner(a, z - dz);
for (int m = 1; m < n - 1; ++m)
{
eval pztry = horner(a, z - complex<double>(m + 1) * dz);
if (pztry.apz >= pzbest.apz)
break; // no improvement
pzbest = pztry;
}
return pzbest;
};
// Set fixed initial start value for each root as an inward spiral from 1
z = complex<double>(0.4, 0.9);
for (i = 0; i < n; i++)
{
roots.push_back(z * pow(z, i));
W[i]=roots.back();
pz.push_back(horner(coeff, roots.back()));
}
if (stage1 == TestConvergence(roots, W))
stage1 = !stage1;
// Start iteration and stop when all roots have been found
for (itercnt = 1; found<n && itercnt < MAX_ITER; itercnt++)
{
double q; // Convergence power q
complex<double> prevW; // Used for q calculation
for ( i = 0; i < n; ++i) // Improve each root if not flagged as finish
{
if (finish[i] == true)
continue;
bool qcheck = false;
// Calculate new root approximation
complex<double> w(1);
z= roots[i]; // Current root to improve
// Calculate the Weierstrass modification
for (int j = 0; j < n; ++j)
{
if (i != j)
w *= (z - roots[j]);
}
prevW = W[i]; // Save previous W[i]
W[i] = pz[i].pz/(w); // Compute new W[i]=P(z)/(w)
// New root
roots[i] -= W[i];
pz[i] = horner(coeff, roots[i]); // Calculate P(roots[i])
// Check if we need to recalculate a precise upperbound e.g. Adams test
if (pz[i].apz < epsLow || stage1 == false)
{ // Calculate final upper bound for the root now that we are getting close
// or convergence test terminates stage1
upper[i] = upperbound(coeff, z);
qcheck = true; // set to trick the test of the Newton option
}
// Calculate convergence power q
q = log(abs(W[i])) / log(abs(prevW));
// When q<1.4 we need to check for multiplicity>1 using the Newton method
// unless stopping criteria have already been fulfilled
// Be aware after one Newton Step the q reflects the convergence power
// of Newton not the Weierstrass step
// This can lead to a false not needed Newton try step.
if (z - W[i] != z && pz[i].apz >= upper[i] && qcheck &&
(abs(q) < 1.4 || NewtonTry[i]))
{
if (coeffprime.size() == 0)
// Calculate coefficients of p'(x), only once if needed
for (int j = 0; j < n; ++j)
coeffprime.push_back(coeff[j] * double(n - j));
NewtonTry[i] = false;
eval p1z = horner(coeffprime, z), p0z = horner(coeff, z);
eval pzbest = MultipleNewtonSteps(coeff, z, p0z.pz / p1z.pz);
if (pzbest.apz < pz[i].apz)
{ // Newton gave an improvement for multiplicity>1
roots[i] = pzbest.z;
pz[i] = pzbest;
W[i] = pzbest.z - z; // Save the step size
NewtonTry[i] = true;
}
}
else
NewtonTry[i] = false;
if (z - W[i] == z || pz[i].apz < upper[i])
{ // Root is found
eval pz0;
// flag current root as finish
finish[i] = true;
++found;
// Finalize root
z = abs(z.real())>=abs(z.imag())?
complex<double>(z.real(),0): complex<double>(0,z.imag());
pz0 = horner(coeff, z);
if (pz0.apz <= pz[i].apz)
{
pz[i] = pz0;
roots[i] = z;
}
}
}
if (stage1 == TestConvergence(roots, W))
stage1 = !stage1;
}
return roots;
}
示例 1
以下是上述源代码工作方式的示例。
对于实数多项式
+1x^4-10x^3+35x^2-50x+24
开始 Durand-Kerner 迭代,用于多项式=+1x^4-10x^3+35x^2-50x+24
初始停止条件。 |f(z)|<2.13e-14
Start
z[1]=1 dz=1.00e+0 |f(z)|=0.0e+0
z[2]=(0.4+i0.9) dz=(4.00e-1+i9.00e-1) |f(z)|=2.0e+1
z[3]=(-0.7+i0.7) dz=(-6.50e-1+i7.20e-1) |f(z)|=8.7e+1
z[4]=(-0.9-i0.3) dz=(-9.08e-1-i2.97e-1) |f(z)|=1.1e+2
迭代:1
1 次迭代后满足停止标准
找到一个根 z[1]=1 |f(x)|=0.00e+0
变化=0%
z[2]=(-4-i8) dz=(4.14e+0+i9.02e+0) |f(z)|=1.1e+4
z[3]=(-6+i0.9) dz=(4.89e+0-i1.40e-1) |f(z)|=4.1e+3
z[4]=(0.1-i1) dz=(-1.05e+0+i9.56e-1) |f(z)|=4.3e+1
迭代:2
z[2]=(1e+1-i1e+1) dz=(-1.60e+1+i2.97e+0) |f(z)|=4.8e+4
z[3]=(-2+i4) dz=(-3.84e+0-i2.88e+0) |f(z)|=9.9e+2
z[4]=(0.5-i1) dz=(-3.41e-1-i2.60e-2) |f(z)|=2.7e+1
迭代:3
z[2]=(8-i2) dz=(4.25e+0-i8.67e+0) |f(z)|=1.3e+3
z[3]=(2+i3) dz=(-3.27e+0+i1.09e+0) |f(z)|=7.8e+1
z[4]=(1-i1) dz=(-6.28e-1-i2.13e-1) |f(z)|=9.1e+0
迭代:4
z[2]=(5.5-i1.0) dz=(2.58e+0-i1.42e+0) |f(z)|=7.7e+1
z[3]=(3+i2) dz=(-9.58e-1+i1.12e+0) |f(z)|=1.2e+1
z[4]=(2-i0.6) dz=(-5.74e-1-i4.04e-1) |f(z)|=2.2e+0
迭代:5
z[2]=(4.4-i0.49) dz=(1.03e+0-i5.02e-1) |f(z)|=8.4e+0
z[3]=(3+i0.7) dz=(-3.01e-1+i8.04e-1) |f(z)|=2.2e+0
z[4]=(2-i0.2) dz=(-3.17e-1-i3.82e-1) |f(z)|=4.8e-1
迭代:6
z[2]=(4.0-i0.20) dz=(4.00e-1-i2.95e-1) |f(z)|=1.3e+0
z[3]=(3+i0.1) dz=(-1.18e-1+i5.77e-1) |f(z)|=3.1e-1
z[4]=(2.0+i0.00025) dz=(-1.28e-2-i2.28e-1) |f(z)|=2.3e-2
迭代:7
z[2]=(3.98-i0.0185) dz=(4.49e-2-i1.81e-1) |f(z)|=1.6e-1
z[3]=(3.0-i0.0031) dz=(-5.83e-2+i1.48e-1) |f(z)|=1.1e-2
z[4]=(2.00-i0.000149) dz=(1.18e-2+i3.95e-4) |f(z)|=3.2e-4
迭代:8
z[2]=(4.000+i0.00001949) dz=(-1.97e-2-i1.85e-2) |f(z)|=8.7e-4
z[3]=(3.00+i8.52e-8) dz=(4.26e-3-i3.06e-3) |f(z)|=2.8e-6
z[4]=(2.0000-i1.1529e-8) dz=(-6.13e-5-i1.49e-4) |f(z)|=2.4e-8
迭代:9
9 次迭代后满足停止标准
找到一个根 z[4]=1.9999999999999971 |f(x)|=2.40e-18
变化=0%
z[2]=(4.00000-i3.84657e-11) dz=(1.44e-4+i1.95e-5) |f(z)|=1.2e-9
z[3]=(3.000000+i1.619904e-14) dz=(1.39e-6+i8.52e-8) |f(z)|=3.3e-14
迭代:10
10 次迭代后满足停止标准
找到一个根 z[2]=3.9999999999999964 |f(x)|=2.13e-14
变化=0%
10 次迭代后满足停止标准
找到一个根 z[3]=2.9999999999999947 |f(x)|=6.31e-30
变化=0%
使用 Durand-Kerner 方法,解决方案是:
X1=1.9999999999999971
X2=2.9999999999999947
X3=3.9999999999999964
X4=1
示例 2
对于实数多项式
+1x^4-8x^3-17x^2-26x-40
开始 Durand-Kerner 迭代,用于多项式=+1x^4-8x^3-17x^2-26x-40
初始停止条件。 |f(z)|<3.55e-14
Start
z[1]=1 dz=1.00e+0 |f(z)|=9.0e+1
z[2]=(0.4+i0.9) dz=(4.00e-1+i9.00e-1) |f(z)|=4.7e+1
z[3]=(-0.7+i0.7) dz=(-6.50e-1+i7.20e-1) |f(z)|=2.9e+1
z[4]=(-0.9-i0.3) dz=(-9.08e-1-i2.97e-1) |f(z)|=2.5e+1
迭代:1
z[1]=(9+i2e+1) dz=(-7.78e+0-i2.26e+1) |f(z)|=3.3e+5
z[2]=(0.1+i2) dz=(2.88e-1-i1.03e+0) |f(z)|=4.4e+1
z[3]=(-1+i0.8) dz=(8.08e-1-i9.07e-2) |f(z)|=3.8e+1
z[4]=(-0.9-i0.6) dz=(-5.56e-2+i3.28e-1) |f(z)|=2.9e+1
迭代:2
z[1]=(1e+1-i2) dz=(-2.29e+0+i2.44e+1) |f(z)|=3.5e+3
z[2]=(0.1+i1) dz=(1.69e-2+i7.20e-1) |f(z)|=2.5e+1
z[3]=(-1-i0.3) dz=(-3.15e-1+i1.15e+0) |f(z)|=2.2e+1
z[4]=(2-i2) dz=(-2.50e+0+i1.34e+0) |f(z)|=2.4e+2
迭代:3
z[1]=(9.9+i0.61) dz=(1.18e+0-i2.36e+0) |f(z)|=7.4e+2
z[2]=(0.2+i2) dz=(-8.43e-2-i3.61e-1) |f(z)|=2.7e+1
z[3]=(-1.3-i0.13) dz=(1.72e-1-i2.07e-1) |f(z)|=1.5e+1
z[4]=(-0.4-i2) dz=(2.08e+0-i4.07e-1) |f(z)|=1.7e+1
迭代:4
z[1]=(10-i0.025) dz=(-1.12e-1+i6.33e-1) |f(z)|=3.1e+1
z[2]=(-0.2+i2) dz=(3.73e-1+i1.23e-3) |f(z)|=1.9e+0
z[3]=(-2-i0.03) dz=(3.76e-1-i9.92e-2) |f(z)|=2.8e+0
z[4]=(-0.18-i1.6) dz=(-2.53e-1-i1.56e-3) |f(z)|=5.2e-1
迭代:5
z[1]=(10.00-i0.0001396) dz=(2.37e-3-i2.50e-2) |f(z)|=1.8e-1
z[2]=(-0.175+i1.55) dz=(-1.77e-2+i2.03e-2) |f(z)|=4.8e-2
z[3]=(-1.7+i0.000043) dz=(-3.97e-2-i3.07e-2) |f(z)|=9.0e-3
z[4]=(-0.175-i1.55) dz=(-1.54e-3-i7.45e-3) |f(z)|=1.6e-4
迭代:6
z[1]=(10.0000-i1.10034e-8) dz=(5.34e-5-i1.40e-4) |f(z)|=1.5e-5
z[2]=(-0.1747+i1.547) dz=(-3.62e-4+i5.99e-4) |f(z)|=3.8e-6
z[3]=(-1.6506+i1.1970e-10) dz=(-1.63e-4+i4.35e-5) |f(z)|=9.8e-9
z[4]=(-0.1746854-i1.546869) dz=(6.66e-7-i2.18e-6) |f(z)|=2.8e-12
迭代:7
7 次迭代后满足停止标准
找到一个根 z[2]=(-0.17468540428030596+i1.5468688872313963) |f(x)|=7.11e-15
变化=0%
7 次迭代后满足停止标准
找到一个根 z[3]=-1.6506291914393882 |f(x)|=2.13e-14
变化=0%
7 次迭代后满足停止标准
找到一个根 z[4]=(-0.17468540428030596-i1.5468688872313963) |f(x)|=7.11e-15
变化=0%
z[1]=(10.00000000+i4.467037524e-17) dz=(-4.71e-9-i1.10e-8) |f(z)|=5.5e-12
迭代:8
8 次迭代后满足停止标准
找到一个根 z[1]=10 |f(x)|=1.90e-28
变化=0%
使用 Durand-Kerner 方法,解决方案是:
X1=(-0.17468540428030596-i1.5468688872313963)
X2=-1.6506291914393882
X3=(-0.17468540428030596+i1.5468688872313963)
X4=10
其他不使用导数的类 Weierstrass 联立方法
Durand-Kerner 还有一些衍生方法。Tanabe [12] 的三阶方法

它提供了三阶收敛率。
还有 Nourein [12] 的四阶方法,也基于 Weierstrass 校正。

有了这里提供的 Durand-Kerner 方法,实现这两个衍生方法相对简单。
Aberth-Erhlich 联立方法
另一个密切相关的方法是 1967 年的 Aberth-Erhlich [13] 方法。该方法也同时找到所有根,但需要使用多项式的一阶导数 P'(x)。
这是一个非常稳健的方法,并且已在 MPSolve 软件包中实现。它是一种三阶收敛方法,尽管它处理重数大于一的根时仅具有线性收敛。Aberth-Ehrlich 效率指标为 3(1/2)=1.73。

Aberth 在其原始论文 [13] 中也描述了所有根的合适起点。
建议
尽管 Durand-Kerner 方法的效率指标高于牛顿法,但通常不建议使用改进的 Durand-Kerner 方法而不是牛顿法。在我看来,原因在于第一部分和第二部分中提出的改进牛顿法通常能更快地趋近于根,因此比 Durand-Kerner 使用更少的迭代。我建议坚持使用第一部分和第二部分中介绍的牛顿法。然而,如果您决定使用 Durand-Kerner,它仍然是选择一个良好且高效的多项式求根方法的可靠选择。
结论
我们提出了一个改进的 Durand-Kerner 方法,它建立在第一部分和第二部分建立的框架之上,尽管 Durand-Kerner 方法非常不同。第六部分将展示集成替代多点方法的便捷性。一个展示这些各种方法的基于 Web 的多项式求解器可供进一步探索,并且可以在“多项式根”找到,该页面展示了许多这些方法的实际应用。
参考文献
- H. Vestermark. A practical implementation of Polynomial root finders. hvks.com/Numerical/Downloads/HVE Practical Implementation of Polynomial root finders.pdf
- Madsen. A root-finding algorithm based on Newton Method, Bit 13 (1973) 71-75。
- A. Ostrowski, Solution of equations and systems of equations, Academic Press, 1966。
- Wikipedia Horner’s Method: https://en.wikipedia.org/wiki/Horner%27s_method
- Adams, D A stopping criterion for polynomial root finding. Communication of the ACM Volume 10/Number 10/ October 1967 Page 655-658
- Grant, J. A. & Hitchins, G D. Two algorithms for the solution of polynomial equations to limiting machine precision. The Computer Journal Volume 18 Number 3, pages 258-264
- Wilkinson, J H, Algebraic Processes中的舍入误差, Prentice-Hall Inc, Englewood Cliffs, NJ 1963
- McNamee, J.M., Numerical Methods for Roots of Polynomials, Part I & II, Elsevier, Kidlington, Oxford 2009
- H. Vestermark, “A Modified Newton and higher orders Iteration for multiple roots.”, www.hvks.com/Numerical/papers.html
- M.A. Jenkins & J.F. Traub, ”A three-stage Algorithm for Real Polynomials using Quadratic iteration”, SIAM J Numerical Analysis, Vol. 7, No.4, December 1970。
- H.A. Yamani, A.D. Alhaidari, Iterative polynomial-root-finding procedure with enhanced accuracy, Saudi Center for Theoretical Physics, Saudi Arabia。
- M. Petkovic, D. Herceg, S.Ilic, Safe convergence of simultaneous methods for polynomial zeros. Numeric Algorithm 17 (1998) 313-3312
- O. Aberth, Iteration Methods for finding all zeros of a Polynomial Simultaneously, Mathematics Computation, Vol 27, Number 122, April 1973
历史
- 2023年12月20日:初始版本
