65.9K
CodeProject 正在变化。 阅读更多。
Home

通过简单示例理解时间复杂度

Nicolas DESCARTES
starIconstarIconstarIconstarIcon
emptyStarIcon
starIcon

4.17/5 (6投票s)

2023年11月23日

CPOL

8分钟阅读

viewsIcon

9932

什么是计算机科学中的时间复杂度？如何确定给定算法的时间复杂度？

引言

每个人都欣赏计算机能够快速完成任务的能力。人们普遍期望计算机能够响应迅速且性能卓越。然而，计算机的每一项任务背后都有一系列指令，这些指令必须按特定顺序执行。在此框架内，指令的定义方式可能存在差异，因此需要探索比其他方法更有效的方法。那么问题就来了：如何确定一种方法比另一种方法更优越呢？

有三本关于此主题的权威教科书值得参考。它们被广泛认为是标准参考书，并在课程中普遍使用。

那么，如何确定一种方法比另一种方法更优越呢？

实际上，这个问题没有一个单一的确定性答案，因为“优越”一词对每个人来说可能意味着不同的东西。有些人认为，如果一种方法占用的内存空间更少，那么它就更优越，这对于内存管理至关重要的设备（如微控制器）尤其重要。另一些人可能认为，如果一种方法易于理解和解释，那么它就更优越。在本系列中，我们将把一种方法定义为更优越，如果它仅仅比其他方法执行所需的时间更少。

在我们继续之前，让我们先澄清一些术语：计算机在有限的时间内处理一系列有限的任务或指令以获得结果，这非正式地称为 **算法**。因此，我们的目标是，在几种算法中，确定哪些算法更适合更早地终止。这种对算法执行任务所需时间的分析被称为时间复杂度，并且自计算机科学早期以来就至关重要。

如何衡量和比较时间复杂度？

因此，时间复杂度是衡量算法完成任务所需时间的一种度量，**该度量基于其输入的大小**。它提供了算法运行所需的计算时间的估计，作为输入大小的函数。计算机科学家普遍使用大O符号来描述时间复杂度，而我们在本节的目标是阐明该符号的含义。

非正式地，什么是大O符号？

设想我们被要求设计一个处理包含 5 个整数的数组的程序（程序的具体内容无关紧要）。实现后，我们进行自然测试，并观察到程序执行需要 5 秒。随后，我们将输入修改为使用包含 10 个整数的数组，用这些新参数运行程序，并发现现在执行需要 10 秒。从这个观察中，我们可以推断，如果我们想将输入大小加倍，执行时间也会加倍：执行时间与输入的关系是线性的。

现在，设想我们深入研究文献，找到了实现此程序的替代方法。掌握了这种新方法后，我们重新实现了之前的算法，再次进行测试，并注意到使用 5 个整数现在需要 0.5 秒，使用 10 个整数则需要 1 秒。由此，我们再次可以推断，如果我们想将输入大小加倍，执行时间也会加倍：执行时间与输入的关系仍然是线性的。

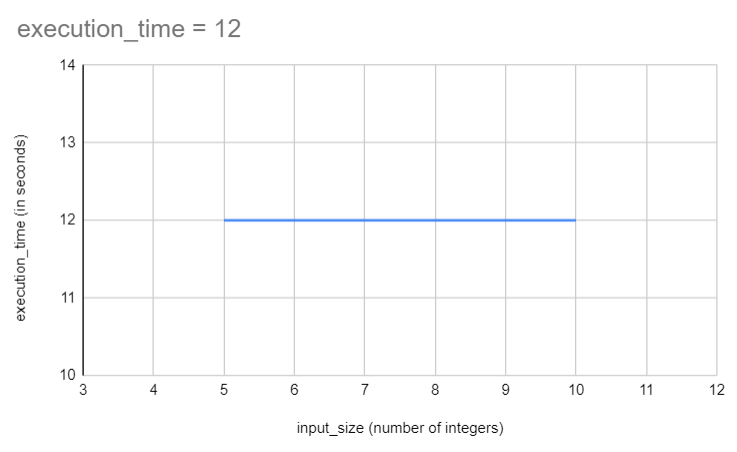
事实上，乍一看，第二种方法似乎更优越，因为它在相同的输入下花费的时间更少。然而，在深入研究其他研究论文后，我们遇到了一种新算法。虽然它稍微复杂一些，但使用包含 5 个整数的数组执行需要 12 秒，并且令人惊讶的是，使用包含 10 个整数的数组也需要 12 秒。这种方法似乎明显不利。它不仅实现起来更困难，而且执行所需的时间也更长！

带着更高的意识，我们继续在实际条件下进行实验，使用包含 1000 个整数的数组。正如预期的那样，第一种方法执行需要 1000 秒，而第二种方法执行需要 100 秒。然而，非常令人惊讶的是，第三种算法再次只花费了 12 秒。现在，这种第三种算法的性能远远优于其他算法！

从这个例子中可以得出几个关键的见解。

  • 首先，算法的优越性只能通过渐近数据有意义地研究和比较，特别是随着输入规模越来越大。前面提到的第三种方法以常数时间运行，无论输入大小如何都能保持一致的性能，而其他两种算法的时间复杂度与输入成正比。
  • 其次，尽管第二种算法的运行速度可能比第一种算法快，但对于更大的输入，这种差异变得不那么重要了。关键的考虑因素是其时间复杂度仍然与传递参数的大小成线性关系。

非正式地说，我们会说第三种算法以常数时间执行，或者是一个 O(1) 算法。另一方面，第一种和第二种算法以线性时间执行，是 O(n) 算法。

简而言之，大O符号使开发人员和研究人员能够以独立于语言和平台的方式比较算法的效率。它侧重于算法的高级行为，在分析算法对于大型输入规模的可伸缩性时特别有用。请记住，虽然大O符号提供了上限，但它并未捕获常数因子、低阶项或实现的具体细节。

那么，正式地，什么是大O符号？

我们在本文中没有深入探讨细节，但大O符号在有数学背景的情况下可以完全严谨。

更多信息可以在 这里 找到。

常见的大O符号有哪些？

以下是一些常见的大O符号

  • O(1) - 时间复杂度是常数，与输入大小无关。这些算法通常是最好的。
  • O(logn) - 时间复杂度随输入大小呈对数增长。这些算法非常受欢迎。
  • O(n) - 时间复杂度与输入大小成正比。
  • O(nlogn) - 时间复杂度被称为线性对数（linearithmic），在归并排序和快速排序等高效排序算法中很常见。
  • O(n^2) - 时间复杂度与输入大小的平方成正比（二次方）。在效率较低的排序算法中很常见。
  • O(2^n) - 时间复杂度是指数级的，运行时间随输入大小迅速增长。这些算法在大型输入上通常是无用的，必须避免。

理论够了，来点例子！

现在我们将通过比较计算实数幂的各种算法来提供一个具体的示例。我们将演示某些方法比其他方法效率更高。

给定实数 x 和整数 n，我们的目标是以高效的方式计算 xn。代码将用 C# 编写，但自然，它也适用于所有其他编程语言。

我们将首先定义一个所有算法都将实现的 IComputePower 接口。

public interface IComputePower
{
    double ComputePower(double real, int power);
}

算法 1

第一个算法非常直接，无需进一步解释：我们只是应用幂的数学定义。

public class LinearComputePower : IComputePower
{
    public double ComputePower(double real, int power)
    {
        var y = 1.0;
        for (var i = 0; i < power; i++)
        {
            y *= real;
        }

        return y;
    }
}

算法分析

我们将 T1​(n) 表示为程序执行过程中执行的乘法次数。从代码中可以看出，T1​(n)=n​（因为在 for 循环中执行了 n 次乘法）。

T1​(n)=O(n)​

算法 2

第二个算法只是第一个算法的递归变体。

public class LinearRecursiveComputePower : IComputePower
{
    public double ComputePower(double real, int power)
    {        
        if (power == 0) return 1.0;
        return real * ComputePower(real, power-1);
    }
}

算法分析

我们将 T2​(n) 表示为程序执行过程中执行的乘法次数。从算法的递归形式，我们可以将 T2​(n) 表示为 T2​(n)=1+T2​(n−1) （对于所有 n≥1，且 T(0)=1）。这形成了一个与代码的递归方面相呼应的归纳关系。这个归纳关系的求解非常直接，T2​(n)=n。

T2​(n)=O(n)​

算法 3

我们正在研究的第三种算法是一种更复杂的计算方法，基于以下事实：如果 n 是偶数，则 xn=(x2)n/2；如果 n 是奇数，则 xn=x(x2)(n-1)/2​。这提供了一种可以递归实现的二分法。

public class DichotomyComputePower : IComputePower
{
    public double ComputePower(double real, int power)
    { 
        if (power == 0) return 1.0;
        if (power == 1) return real;
        else
        {
            if (power % 2 == 0) return ComputePower(real*real, power/2);
            else return real * ComputePower(real*real, (power-1)/2);
        }
    }
}

我们将 T3​(n) 表示为程序执行过程中执行的乘法次数。我们不会深入研究细节，但时间复杂度可以通过一些相当复杂的数学精确确定（有关完整证明，请参阅 此处）。在此，我们只承认 **T3(n)=O(log2n)**。

该算法似乎具有非常理想的执行时间，并且优于其他算法。

如何验证我们的分析？

在最后一部分，我们将尝试证明我们之前的理论计算与实际相符。为此，我们将有意在算法中引入一个 Thread.Sleep 指令，每次执行乘法时，然后我们将使用各种 n 值来执行这些算法。

例如，这是我们的算法如何通过此指令进行修改。

public class DichotomyComputePower : IComputePower
{
    public double ComputePower(double real, int power)
    {
        Thread.Sleep(1000);

        if (power == 0) return 1.0;
        if (power == 1) return real;
        else
        {
            if (power % 2 == 0) return ComputePower(real*real, power/2);
            else return real * ComputePower(real*real, (power-1)/2);
        }
    }
}

主程序将使用一个监视器来计算执行时间。

public static void Main(string[] args)
{
    var watch = new Stopwatch();
    var x = 2; var n = ...;

    watch.Start();
    
    var computer = new DichotomyComputePower();
    var res = computer.ComputePower(x, n);
    
    watch.Stop();

    Console.WriteLine($"Time elapsed: {watch.ElapsedMilliseconds} ms, result: {res}");
}

以下是各种 n 值的运行结果。

显然，第三种算法的执行速度比其他算法快。这证实了我们之前的分析。

更多示例和本文其余部分可以在 此处 找到。

历史

  • 2023年11月23日：初始版本
© . All rights reserved.