编写自己的正则表达式解析器

Amer Gerzic

4.91/5 (128投票s)

2003年11月10日

22分钟阅读

1085491

12342

解释编写正则表达式解析器背后的原理。

Sample Image - RegExDemo.jpg

引言

你是否曾详细地想过正则表达式是如何工作的？如果答案是肯定的，那么这篇文章就适合你。我将尝试一步一步地指导你如何创建自己的迷你正则表达式库。本文的目的不是为你提供一个高度优化、经过测试且优秀的正则表达式库，而是解释文本文件中模式匹配背后的原理。如果你只需要一个好的库，而不关心它如何工作，你可能需要 Boost regex 库，你可以在这里找到。我使用过几个不同的正则表达式库，但我必须说我最满意 Boost regex。显然，这由你自己决定。CodeProject 上还有另一篇正则表达式文章，可以在这里找到。我必须承认，我没有完全阅读那篇文章，但在我看来，那篇文章主要关注如何使用作者提供的正则表达式库。在这篇文章中，作者使用了类似的技术（尽管我可能错了）来创建一个更复杂的库。你现在正在阅读的这篇文章，可以看作是我刚才提到的那篇文章的先决条件。

正则表达式是 MS .NET 库或 Java SDK 的一部分（如果你用 Java 编写代码）。如你所见，正则表达式在许多不同的编程语言和技术中都可用。实际上，这篇文章不专注于用特定语言编写库。我用 C++ 编写了代码，主要使用 STL，因为它是我最喜欢的语言/库，但文章中的原理可以应用于任何语言（显然）。我将尽量保持语言独立性，尽可能使用伪代码。如果你想要 Java 代码，请给我发电子邮件。本文提供的代码是免费的（显然），但如果你喜欢并在你的应用程序中使用它，如果你能给我应得的荣誉，那就太好了。也请给我发电子邮件，这样我就可以向我的同事和/或潜在雇主炫耀。

概述

那么我们该怎么做呢？在开始编码之前，有必要解释理解本文所用方法所需的数学背景。我强烈建议阅读并理解其背后的数学原理，因为一旦我们克服了数学部分，其余部分将非常简单。但请注意，我不会提供任何数学证明。如果你对证明感兴趣，请查阅本文参考文献部分中的参考资料。此外，请注意，我们将在此处创建的正则表达式解析器将支持以下三种操作：

Kleen 闭包或星号运算符 ("*")
连接（例如："ab"）
联合运算符（用字符 "|" 表示）

然而，许多附加运算符可以通过组合这三个运算符来模拟。例如

A+ = AA* (至少一个 A)
[0-9] = (0|1|2|3|4|5|6|7|8|9)
[A-Z] = (A|B|...|Z) 等。

只实现三个运算符的原因是为了简化。当我开始计划写这篇文章时，我很快意识到我必须在很多方面限制自己。这个话题太大了，需要一本书才能解释每一个细节（也许有一天我会写）。正如我上面所说，本文的目的不是为你提供一个库，而是向你介绍正则表达式背后的原理。如果你想了解更多关于如何使用正则表达式的知识，那么你可以查阅《精通正则表达式 - O'Reilly》这本书。

以下是文章的概述

什么是非确定性有限自动机（NFA）？
什么是确定性有限自动机（DFA）？
Thompson 算法
子集构造算法
DFA 优化
使用上述部分的结果
结束语
参考

什么是非确定性有限自动机（NFA）？

NFA 代表非确定性有限状态自动机。NFA 可以看作是一种特殊类型的有限状态机，它在某种意义上是一种具有原始内部存储器的机器的抽象模型。如果你想了解更多关于有限状态机的信息，请参阅下面的参考文献部分。

让我们看看 NFA 的数学定义。

一个 NFA A 由以下部分组成：

一个有限的输入符号集 I
一个有限的状态集 S
一个从 S x I 到 P(S) 的下一状态函数 f
一个接受状态的 S 子集 Q
一个来自 S 的初始状态 s0

表示为 A(I, S, f, Q, s0)

如果我们向一个12岁的孩子解释上述定义，我们可以说NFA是一组由函数f连接的状态S（也许是对一个更聪明的12岁孩子）。NFA有两种表示形式：表格和图。例如，让我们看看表格表示：

输入状态	a	b	c	d	Epsilon
`s0`	`s1`,`s3`
`s1`		`{s2}`
`{s2}`
`s3`					`s4`,`s5`
`s4`				`{s6}`
`s5`			`{s7}`
`{s6}`
`{s7}`

等效的图表将是

从上面的表格/图中可以看出，有一些特殊的转换称为 Epsilon 转换，这是 NFA 的一个特殊特性。转换是从一个状态到另一个状态的事件。Epsilon 转换是在空字符串上从一个状态到另一个状态的转换。换句话说，我们在没有字符输入的情况下从一个状态到另一个状态。例如，从上面的表格/图中我们可以看到，我们可以在没有输入的情况下从 s3 到 s4 和 s5，这意味着我们有一个选择。同样，在字符输入 a 上，从状态 s0 到状态 s1 或 s3 也有一个选择。因此得名非确定性，因为在某些时候，我们能够走的路径不是唯一的，而是我们有一个选择。最终和接受状态用双圆圈（或在表格中用 "{}" 括起来）表示，例如 s6。一旦达到其中一个状态，我们就有一个接受状态，从而有一个接受的字符串。

在一个 NFA 中，如数学定义所定义，总是有一个起始状态。我使用 Graphvis，一个用于绘制各种图表的出色工具（请参阅参考文献部分），来绘制 NFA 和 DFA（稍后会讲到）。由于 Graphvis 会自动布置图的节点，在我看来，起始状态总是绘制在图顶部的状态。所以我们将遵循这个约定。

什么是确定性有限自动机（DFA）？

DFA 代表确定性有限状态自动机。DFA 与 NFA 密切相关。事实上，NFA 的数学定义也适用于 DFA。但显然存在差异，我们将利用这些差异。一个很大的区别是 DFA 中没有 Epsilon 转换。此外，对于每个状态，所有从该状态引出的转换都在不同的输入字符上进行。换句话说，如果我们在状态 s 中，那么在输入字符 a 上，从 s 到该字符的转换是唯一的。此外，在 DFA 中，所有状态都必须具有在输入字符上的有效转换。这里的输入字符是输入符号的有限集 I（如数学定义中所示）。例如，在上面的图（DFA 下）中，符号集 I 将是 {a,b,c,d}。

既然我们已经理解了 NFA 和 DFA，我们就可以继续说，给定任何 NFA，都存在一个等价的 DFA（你必须相信我这一点，因为我认为提供这个陈述的数学证明不合适）。作为人类，通常我们更容易构造一个 NFA，也更容易解释 NFA 接受的语言。但我们为什么还需要 DFA 呢？嗯，如果我们考虑计算机，让它们做出非常“明智的猜测”是非常困难的（有时甚至我们都无法做出明智的猜测）。而这正是计算机在遍历 NFA 时需要做的。如果我们编写一个算法，使用 NFA 来检查字符的接受组合，它将涉及回溯以检查以前未做出的选择。显然，有些正则表达式解析器使用 NFA 工作，但它们通常比使用 DFA 的解析器慢。这是因为 DFA 对于每个接受的字符串都有唯一的路径，因此不涉及回溯。因此，我们将使用 DFA 来检查自动机是否接受输入字符的组合。

注意：如果你真的想理解 NFA 和 DFA，我建议你进一步阅读这些主题。作为一种练习，将它们相互转换有助于完全理解其差异以及这里用于将 NFA 转换为 DFA 的算法（见后文）。

Thompson 算法

现在我们已经具备了理解正则表达式所需的所有数学背景知识，我们需要开始思考我们的目标是什么。第一步，我们意识到我们需要一种方法，将正则表达式（如 ab*(a|b)*）转换为一种易于操作和用于模式匹配的数据结构。但我们首先来看看将正则表达式转换为 NFA 的方法。最著名的转换算法可能是 Thompson 算法。该算法不是最有效的，但它确保任何正则表达式（假设其语法正确）都能成功转换为 NFA。借助下图所示的基本 NFA，我们可以构造任何其他 NFA：

利用上面的基本元素，我们将构建我们希望在正则表达式解析器中实现的三个操作，如下所示

但是我们如何从像 (a|b)*ab 这样的表达式转换成上面的图呢？如果我们考虑我们真正需要做的事情，我们会发现评估正则表达式类似于评估算术表达式。例如，如果我们想评估 R=A+B*C-D，我们可以这样做：

PUSH A

PUSH B

PUSH C

MUL

ADD

PUSH D

SUB

POP R

这里 PUSH 和 POP 是栈操作，MUL、ADD 和 SUB 从栈中取出 2 个操作数并执行相应的操作。我们可以利用这些知识从正则表达式构造 NFA。让我们看看从正则表达式 (a|b)*cd 构造 NFA 需要执行的操作序列：

PUSH a

PUSH b

UNION

STAR

PUSH c

CONCAT

PUSH d

CONCAT

POP R

如我们所见，这与算术表达式的求值非常相似。不同之处在于，在正则表达式中，星号操作只从栈中弹出一个元素并求值星号运算符。此外，连接操作没有用任何符号表示，因此我们必须检测它。文章提供的代码通过预处理正则表达式并在检测到连接时插入字符 ASCII 码 0x8 来简化问题。显然，在正则表达式求值期间“即时”执行此操作是可能的，但我希望尽可能简化求值。预处理除了检测导致连接的符号组合（例如：ab、a(、)a、*a、*(、)(）之外，什么也不做。

PUSH 和 POP 操作实际上与一个简单的 NFA 对象栈一起工作。如果我们 PUSH 符号 a 到栈上，该操作将在堆上创建两个状态对象，并在符号 a 上从状态 1 到状态 2 创建一个转换对象。这是将字符推入栈的代码片段：

void CAG_RegEx::Push(char chInput)
{
    // Create 2 new states on the heap
    CAG_State *s0 = new CAG_State(++m_nNextStateID);
    CAG_State *s1 = new CAG_State(++m_nNextStateID);

    // Add the transition from s0->s1 on input character
    s0->AddTransition(chInput, s1);

    // Create a NFA from these 2 states 
    FSA_TABLE NFATable;
    NFATable.push_back(s0);
    NFATable.push_back(s1);

    // push it onto the operand stack
    m_OperandStack.push(NFATable);

    // Add this character to the input character set
    m_InputSet.insert(chInput);
}

如我们所见，字符被转换为一个简单的 NFA，然后生成的 NFA 被添加到堆栈中。CAG_State 类是一个简单的类，它帮助我们根据需要构造 NFA。它包含一个在特定字符上转换到其他状态的数组。Epsilon 转换是在字符 0x0 上的转换。此时，很容易看出 NFA 背后的结构。NFA（和 DFA）存储为一系列状态（deque 类型的 CAG_State 指针）。每个状态都将所有存储在 multimap 中的转换作为成员。转换无非是从字符到状态（CAG_State*）的映射。有关 CAG_State 类的详细定义，请参阅代码。

现在回到从正则表达式到NFA的转换。既然我们知道如何将NFA推入栈中，那么弹出操作就非常简单了。只需从栈中取出NFA即可。正如我之前所说，NFA表被定义为一个双端队列（STL容器deque<CAG_State*>）。通过这种方式，我们知道数组中的第一个状态始终是起始状态，而最后一个状态是最终/接受状态。通过保留此顺序，我们可以快速获取第一个和最后一个状态，并在执行操作（如星号运算符）时追加和前置附加状态。以下是评估每个单独操作的代码：

BOOL CAG_RegEx::Concat()
{
    // Pop 2 elements
    FSA_TABLE A, B;
    if(!Pop(B) || !Pop(A))
        return FALSE;

    // Now evaluate AB
    // Basically take the last state from A
    // and add an epsilon transition to the
    // first state of B. Store the result into
    // new NFA_TABLE and push it onto the stack
    A[A.size()-1]->AddTransition(0, B[0]);
    A.insert(A.end(), B.begin(), B.end());

    // Push the result onto the stack
    m_OperandStack.push(A);
    
    return TRUE;
}

如我们所见，连接操作从堆栈中弹出两个 NFA。第一个 NFA 被改变，因此它现在是新的 NFA，然后被推入堆栈。请注意，我们首先弹出第二个操作数。这是因为在正则表达式中，操作数的顺序很重要，因为 AB != BA（不可交换）。

BOOL CAG_RegEx::Star()
{
    // Pop 1 element
    FSA_TABLE A, B;
    if(!Pop(A))
        return FALSE;

    // Now evaluate A*
    // Create 2 new states which will be inserted 
    // at each end of deque. Also take A and make 
    // a epsilon transition from last to the first 
    // state in the queue. Add epsilon transition 
    // between two new states so that the one inserted 
    // at the begin will be the source and the one
    // inserted at the end will be the destination
    CAG_State *pStartState    = new CAG_State(++m_nNextStateID);
    CAG_State *pEndState    = new CAG_State(++m_nNextStateID);
    pStartState->AddTransition(0, pEndState);

    // add epsilon transition from start state to the first state of A
    pStartState->AddTransition(0, A[0]);

    // add epsilon transition from A last state to end state
    A[A.size()-1]->AddTransition(0, pEndState);

    // From A last to A first state
    A[A.size()-1]->AddTransition(0, A[0]);

    // construct new DFA and store it onto the stack
    A.push_back(pEndState);
    A.push_front(pStartState);

    // Push the result onto the stack
    m_OperandStack.push(A);

    return TRUE;
}

星号运算符从栈中弹出一个元素，根据 Thompson 规则（见上文）对其进行更改，然后将其推入栈中。

BOOL CAG_RegEx::Union()
{
    // Pop 2 elements
    FSA_TABLE A, B;
    if(!Pop(B) || !Pop(A))
        return FALSE;

    // Now evaluate A|B
    // Create 2 new states, a start state and
    // a end state. Create epsilon transition from
    // start state to the start states of A and B
    // Create epsilon transition from the end 
    // states of A and B to the new end state
    CAG_State *pStartState    = new CAG_State(++m_nNextStateID);
    CAG_State *pEndState    = new CAG_State(++m_nNextStateID);
    pStartState->AddTransition(0, A[0]);
    pStartState->AddTransition(0, B[0]);
    A[A.size()-1]->AddTransition(0, pEndState);
    B[B.size()-1]->AddTransition(0, pEndState);

    // Create new NFA from A
    B.push_back(pEndState);
    A.push_front(pStartState);
    A.insert(A.end(), B.begin(), B.end());

    // Push the result onto the stack
    m_OperandStack.push(A);

    return TRUE;
}

最后，联合操作弹出两个元素，进行转换，然后将结果推入栈中。请注意，这里我们必须注意操作的顺序。

最后，我们现在能够评估正则表达式了。如果一切顺利，我们将在堆栈上有一个单个 NFA，这将是我们的结果 NFA。这是利用上述函数的代码。

BOOL CAG_RegEx::CreateNFA(string strRegEx)
{
    // Parse regular expresion using similar 
    // method to evaluate arithmetic expressions
    // But first we will detect concatenation and
    // insert char(8) at the position where 
    // concatenation needs to occur
    strRegEx = ConcatExpand(strRegEx);

    for(int i=0; i<strRegEx.size(); ++i)
    {
        // get the charcter
        char c = strRegEx[i];
        
        if(IsInput(c))
            Push(c);
        else if(m_OperatorStack.empty())
            m_OperatorStack.push(c);
        else if(IsLeftParanthesis(c))
            m_OperatorStack.push(c);
        else if(IsRightParanthesis(c))
        {
            // Evaluate everyting in paranthesis
            while(!IsLeftParanthesis(m_OperatorStack.top()))
                if(!Eval())
                    return FALSE;
            // Remove left paranthesis after the evaluation
            m_OperatorStack.pop(); 
        }
        else
        {
            while(!m_OperatorStack.empty() && Presedence(c, m_OperatorStack.top()))
                if(!Eval())
                    return FALSE;
            m_OperatorStack.push(c);
        }
    }

    // Evaluate the rest of operators
    while(!m_OperatorStack.empty())
        if(!Eval())
            return FALSE;

    // Pop the result from the stack
    if(!Pop(m_NFATable))
        return FALSE;

    // Last NFA state is always accepting state
    m_NFATable[m_NFATable.size()-1]->m_bAcceptingState = TRUE;

    return TRUE;
}

函数 Eval 实际上是在评估堆栈上的下一个运算符。函数 Eval() 从运算符堆栈中弹出下一个运算符，并使用 switch 语句确定要使用哪个操作。括号也被视为运算符，因为它们决定了评估的顺序。函数 Presedence(char Left, char Right) 确定两个运算符的优先级，如果 Left 运算符的优先级 <= Right 运算符的优先级，则返回 TRUE。请查阅代码以了解实现。

子集构造算法

现在我们知道如何将任何正则表达式转换为NFA，下一步是将NFA转换为DFA。起初，这个过程似乎非常具有挑战性。我们有一个包含零个或多个Epsilon转换的图，以及在单个字符上的多个转换，我们需要一个等效的图，它没有Epsilon转换，并且对于每个接受的输入字符序列都有唯一的路径。就像我说的那样，这似乎非常具有挑战性，但实际上并非如此。数学家们实际上已经为我们解决了这个问题，然后利用这些结果，计算机科学家创建了子集构造算法。我不确定该把功劳归于谁，但子集构造算法是这样的：

首先，让我们定义两个函数

Epsilon Closure：此函数以一组状态 T 作为参数，并返回另一组状态，其中包含所有可以通过给定集 T 中每个单独状态的 Epsilon 转换到达的状态。
Move：Move 接受一组状态 T 和输入字符 a，并返回可以在给定输入字符上从 T 中所有状态到达的所有状态。

现在使用这两个函数，我们可以执行转换

DFA 的起始状态是通过取 NFA 起始状态的 Epsilon 闭包 来创建的
对于每个新的 DFA 状态，对每个输入字符执行以下操作：
1. 对新创建的状态执行 move 操作
2. 通过取结果 (i) 的 Epsilon 闭包 来创建新状态。请注意，这里我们可能会得到一个已经存在于我们集合中的状态。这将导致一组状态，这些状态将形成新的 DFA 状态。请注意，这里我们从一个或多个 NFA 状态构造一个单个 DFA 状态。
对于每个新创建的状态，执行步骤 2。
DFA 的接受状态是所有包含 NFA 中至少一个接受状态的状态。请记住，我们在这里是从一个或多个 NFA 状态构造一个单个 DFA 状态。

够简单吗？如果不是，请继续阅读。以下是 Aho、Sethi 和 Ullman 所著《编译器 - 原理、技术和工具》一书第 118-121 页上的伪代码。下面的算法与上面的算法等效，但以不同的方式表达。首先，让我们定义 Epsilon Closure 函数：

S EpsilonClosure(T)
{
  push all states in T onto the stack
    initialize result to T
    while stack is not empty
    {
        pop t from the stack
        for each state u with an edge from t to u labeled epsilon
        {
            if u is not in EpsilonClosure(T)
            {
                add u to result
                push u onto the stack
            }
        }
    }
    return result
}

基本上，这个函数的作用是遍历 T 中的所有状态，并检查在没有输入的情况下可以从这些状态到达哪些其他状态。请注意，每个状态至少可以在没有输入的情况下到达一个状态，即它自己。然后，该函数遍历所有这些结果状态，并检查在没有输入的情况下是否有进一步的转换。例如，让我们看看以下内容：

如果我们在状态集合 {s0,s2} 上调用 Epsilon 转换，则结果状态将是 {s0,s2,s1,s3}。这是因为从 s0，我们可以在没有输入的情况下到达 s1，但是从 s1，我们可以在没有输入的情况下到达 s3，所以从 s1 我们可以在没有输入的情况下到达 s3。

现在我们知道 Epsilon 转换是如何工作的，让我们看看将 NFA 转换为 DFA 的伪代码：

D-States = EpsilonClosure(NFA Start State) and it is unmarked
while there are any unmarked states in D-States
{
    mark T
    for each input symbol a
    {
        U = EpsilonClosure(Move(T, a));
        if U is not in D-States
        {
            add U as an unmarked state to D-States
        }
        DTran[T,a] = U
    }
}

最后，DTran 是 DFA 表，等效于 NFA。

在进行下一步之前，让我们手动使用此过程将 NFA 转换为 DFA。如果你想掌握这个过程，我强烈建议你使用此方法执行更多类似的转换。让我们使用子集构造算法将以下 NFA 转换为其对应的 DFA。

使用子集构造算法，我们将执行以下操作（每个新创建的状态将加粗）：

通过取 NFA 起始状态的 epsilon 闭包来创建 DFA 的起始状态。此步骤生成状态集合：{s1,s2,s4}
执行 Move('a', {s1,s2,s4})，结果为集合：{s3,s4}
执行 EpsilonTransition({s3,s4})，它创建一个新的 DFA 状态：{s3,s4}
执行 Move('b', {s1,s2,s4})，结果为集合：{s5}
执行 EpsilonTransition({s5})，它创建新的 DFA 状态：{s5}
注意：这里我们必须记录 2 个新的 DFA 状态 {s3,s4} 和 {s5}，以及 DFA 起始状态 {s1,s2,s4}。我们还必须记录从 {s1,s2,s4} 到 {s3,s4} 的字符 a 上的转换，以及从 {s1,s2,s4} 到 {s5} 的字符 b 上的转换。
执行 Move('a', {s3,s4})，返回：{s4}
执行 EpsilonTransition({s4})，结果为：{s4}
执行 Move('b', {s3,s4})，结果为集合：{s3,s5}
执行 EpsilonTransition({s3,s5})，结果为：{s3,s5}
{s3,s4}->{s4} 在 a 上
{s3,s4}->{s3,s5} 在 b 上
执行 Move('a', {s5})，返回一个空集，因此我们无需检查 Epsilon 转换
执行 Move('b', {s5})，返回一个空集，所以忽略它。
执行 Move('a', {s4})，返回：{s4}。但这不是一个新状态，所以忽略它。但是我们必须记录转换
{s4}->{s4} 在 a 上
执行 Move('b', {s4}) 返回：{s5}
执行 EpsilonTransition({s5}) 返回：{s5} (不是新的，但我们必须记录转换)
{s4}->{s5} 在 b 上
执行 Move('a', {s3,s5})，返回一个空集，所以忽略它。
执行 Move('b', {s3,s5})，生成：{s3}
EpsilonTransition({s3}) 产生：{s3}，一个新的 DFA 状态
{s3,s5}->{s3} 在 b 上
Move('a', {s3}) 是一个空集
Move('b', {s3}) 是 {s3}，它不是新的，但必须记录转换！
{s3}->{s3} 在 b 上

没有新的状态，所以我们完成了。以下是 DFA 的绘制

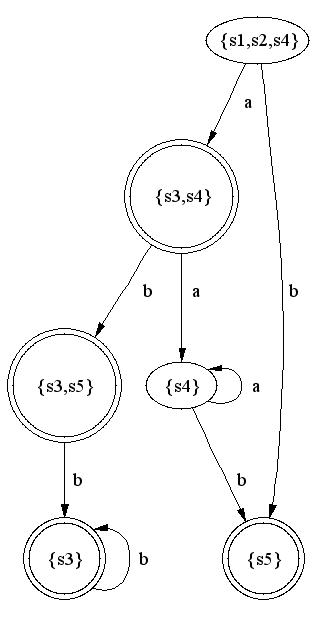
起始状态是 {s1,s2,s4}，因为它是 EpsilonClosure(NFA 的起始状态)。接受状态是 {s5}、{s3,s4} 和 {s3,s5}，因为它们包含 s3 和/或 s5，这些是 NFA 的接受状态。

DFA 优化

现在我们已经掌握了将正则表达式转换为 NFA，然后将 NFA 转换为等效 DFA 的所有知识，我们实际上可以到此为止，并将其用于模式匹配。最初我计划撰写这篇文章时，为了尽可能简单地展示原理，没有考虑 DFA 优化。但后来我意识到，首先对于大型正则表达式，我们创建了非常大的 NFA（根据 Thompson 算法的性质），这反过来偶尔会创建复杂的 DFA。如果我们要搜索模式，这可能会大大减慢我们的速度，因此我决定将优化作为正则表达式解析器的一部分。这里的优化并不复杂。所以我们来看看下面的例子：

如果我们查看这个 DFA，我们会注意到状态 3 首先不是一个最终状态。此外，我们注意到除了循环之外，没有从这个状态发出的出边。换句话说，一旦我们进入状态 3，就没有机会到达一个接受状态。这是因为 DFA 除了每个接受字符串都有唯一的路径并且不包含 Epsilon 转换之外，它还必须在特定状态下对所有输入字符进行转换（这里所有输入字符指的是可能接受的输入字符集。例如：a|b|c，这里的输入字符集是 {a,b,c}）。在这里我们有点滥用数学，以使 DFA 更简单。通过删除状态 3，我们的 DFA 变得更简单，并且它仍然接受相同的模式集。在这种情况下，我们的 DFA 不再完全是 DFA。如果你在问自己为什么这很重要，那么答案是：不重要！至少对我们来说不重要！我们将使用这种非常基本的优化机制来删除所有具有此类特征的状态，从而获得一个更小、更紧凑的 DFA 用于模式匹配。总结一下，我们将删除具有以下特征的状态（以及所有通向这些状态的转换）：

状态不是接受状态
状态没有到任何其他不同状态的转换。

所以结果如下

上面的 DFA 显然比前一个更小。尽管它实际上不是一个 DFA，我仍将它称为 DFA。

使用上述部分的结果

最后，我们准备好使用上面所有部分来匹配一些文本模式。一旦我们有了 DFA，我们所需要做的就是获取一个输入字符并对照起始状态运行它。这是实现此目的的伪代码：

Find(string s)
{
    for each character c in s
    {
        for each active state s
        {
            if there is transition from s on c
            {
                go to the next state t
                if t is accepting state
                {
                    record the pattern 
                }
                mark t as active
            }
            mark s as inactive
        }
        
        if there is transition from starting state on c
        {
            go to the next state s
            if s is accepting state
            {
                record the pattern
            }
            mark s as active
        }
    }
}

上述代码可以在正则表达式类的 Find(...) 函数中找到。为了跟踪活动状态，我使用了一个链表，这样我就可以快速添加和删除活跃/非活跃状态。处理完所有字符后，所有结果都存储在一个向量中，其中包含模式匹配项。使用 FindFirst(...) 和 FindNext(...) 函数，你可以遍历结果。有关如何使用该类的信息，请参阅 CAG_RegEx 类的文档。此外，此时我必须强调，演示程序将完整文件加载到富文本框中，然后在搜索完成后，将其存储到字符串中，并将其作为参数传递给 FindFirst 函数。根据你的 RAM 大小，我建议避免加载大型文件，因为由于使用了虚拟内存，将数据从一个字符串复制到另一个字符串可能需要很长时间。正如我之前所说，该程序旨在展示文本文件中模式匹配的原理。根据时间安排，未来的版本可能会包含一个更完整的正则表达式解析器，它可以搜索任意大小的文件并以不同方式提供结果。

在这一点上，为了文章的完整性，我必须指出，有一种方法可以将正则表达式直接转换为 DFA。这种方法在这里尚未解释，但如果时间允许，将在未来的文章（或文章更新）中提及。此外，还有不同的方法可以从正则表达式构造 NFA。

结束语

好了，就这些！希望你阅读这篇文章和我撰写它一样愉快。请在任何类型的应用程序中使用演示代码，但请在应得之处给予我荣誉。如果你想使用此处提供的演示代码构建一个更完整的库，请将你的添加项副本发送给我。

注意：CAG_RegEx 类包含两个函数 SaveDFATable() 和 SaveNFATable，它们在调试模式下分别将 NFA 和 DFA 保存到 c:\NFATable.txt 和 c:\DFATable.txt。正如其名称所示，这些是 NFA 和 DFA 表。此外，该类还具有函数 SaveNFAGraph() 和 SaveDFAGraph()，它们在调试模式下创建 2 个文件 c:\NFAGraph.dot 和 c:\DFAGraph.dot。这些文件是简单的文本文件，包含使用 Graphviz 绘制这些图的指令（请查看下面的参考 4）。

参考资料及使用工具

《离散数学》- Richard Johnsonbaugh（第五版）
《离散数学及其应用》- Kenneth H. Rosen（第四版）
《编译器 - 原理、技术与工具》- Aho, Sethi 和 Ullman
来自 ATT 的 Graphviz（用于绘制各种图表的工具）。你可以在这里找到它。