65.9K
CodeProject 正在变化。 阅读更多。
Home

多项式方程求解器

Kenneth Haugland
starIconstarIconstarIconstarIcon
emptyStarIcon
starIcon

4.96/5 (46投票s)

2013年2月27日

CPOL

17分钟阅读

viewsIcon

186761

downloadIcon

13347

通过用于实系数的显式公式求解一、二、三、四次多项式，并使用数值 Jenkins-Traub 算法求解具有实系数和复系数的任意次数多项式。

 

介绍 

最近我遇到一个需要用 .NET 求解 4 次多项式方程的情况，令我惊讶的是，我找不到任何用 C# 或 VB .NET 编写的代码，其中包含显式代数公式或 Jenkins-Traub 数值算法。（尽管如此，我确实找到了一些由 Jenkins 本人编写的 FORTRAN 版 Jenkins-Traub 算法的翻译（仍然可以在这里下载：Netlib）。我确实设法混合了一个 C++ 实现，并将其翻译成了 C# 和 VB.NET。为了辩护，我也翻译了 Laurent Bartholdi 的实现，但该实现未包含在本文中。我实际使用的是 David Binner 翻译的 C++ 算法，仅用于实系数。请接受我对这个错误的诚挚道歉。我依赖于 Henrik Vestermark 编写的用于复系数的 C++ 算法。我将这两个应用程序都从 C++ 和 C 转换成了 C# 和 VB 代码。

 

注意：在商业用途中，Jerkins-Traub 算法可能附带许可，请在使用它销售给别人的程序之前查看此项。对于研究和个人使用，没有问题。

 

实现的显式代数公式很棘手，如果你需要其中一个，肯定会让你费心，所以我决定与你分享。我根据下面的评论BenoitAndrieu 进行了一些公式修正。

我还将讲述一段相当长的故事，因为我读了 Mario Livio 的《无解之方程》这本书。书名指的是五次多项式方程无解的故事，但也回顾了低次多项式方程解的历史发展。

我不会解释这些公式是如何推导出来的，因为公式会变得相当冗长，以至于即使是三次方程解法的一部分人 Tartaglia，也难以记住他发现的所有规则。

至于 Jenkins-Traub 数值算法，它已由我完全从 C++ 和 C 版本翻译成 VB.NET 和 C#，并且据我测试，它似乎运行良好。应该提到的是，Jenkins-Traub 算法通常使用显式公式来处理一、二次方程，而对三次及以上方程使用数值逼近。

一阶多项式方程

在数学上很容易求解，所以如果你在这里遇到困难，可能不应该下载代码。我当然说的是形如 2x + 3 = 7 的方程，这个简单的方程称为线性方程，因为在图上（或绘制时）可以表示为直线。


然而，方程背后的故事非常有趣，所以我将带你回到公元前 2000 年 - 公元前 600 年的美索不达米亚巴比伦文明。在这个语境下，“方程”这个词需要谨慎使用，因为巴比伦人实际上并没有使用代数来解决这些方程，而是通过冗长的讨论和逻辑来解决问题。这可能是一种使数学比我们以往任何时候都更困难、更难以理解的方法，尤其是在处理高次多项式方程时。

这种不使用代数来解决数学问题的方式导致巴比伦人无法找到各种数学问题背后的普遍规律或公式。尽管数学问题表述起来很繁琐，但他们确实设法求解了一些（表示未知数同时有 x 和 y 的方程）线性方程组。


巴比伦人似乎不太热衷于编写关于一阶方程的文本，不像埃及人那样，因为巴比伦人认为它过于基础，不值得详细讨论。然而，在埃及，存在着关于该主题的大量手稿，其中呈现了解决某些问题的数学“配方”，就像食谱一样。


应该提到的是，在中国古代的《九章算术》中，我们可以找到至少三个三元一次方程组的解法，考虑到过程的繁琐，这相当了不起。

二阶多项式方程

著名的二阶多项式方程解法的起源实际上未知，但已知巴比伦人确实详细记录了如何求解该方程，但不知道他们从何而来或如何发现它。巴比伦人理解如何求解形如 x^2 - x = 870 的二次方程，并能找到正解，因为解意图用于例如土地测量等问题。然而，他们忽略了有两个正解的这类方程，因为它们被视为不合逻辑的解。这对于非常早期的希腊数学家欧几里得也是如此，他通过几何学而不是代数来求解二次方程。与古代世界的数学知识相比，埃及人则只会求解形如 x^2 = 4 的方程，而不会求解 x^2 + x = 4，并且他们也只能找到正解。


希腊文明很快就借助杰出的数学家丢番图解决了其中一些问题。他有效地改进了解的呈现方式，成为巴比伦语描述方程和现代代数使用方式之间的中间点。他的著作《算术》展示了三种不同类型的二次方程的解法，以及著名的丢番图方程，费马大定理就是其中一个例子。费马确实读过《算术》，并且在这本丢番图的书的页边空白处写下了他著名的最后定理。至于丢番图本人，我们对他知之甚少，甚至无法确定他具体生活在何时，只知道他可能生活在亚历山大，在公元 200 年至 214 年之间或 284 年至 298 年之间。

随着希腊文明的衰落，西方数学进步陷入停滞，沉寂了近千年。数学的进步现在转向东方，他那个时代的伟大数学家之一，印度的 Brahmagupta，他设法求解了丢番图的一些方程，并且是第一个给出包含负数的二阶多项式方程解的人。他认识到负数可以被视为“债务”，正数视为“财富”，非常类似于今天的会计，从而在数学上取得了巨大突破。


求解方程的下一步重大进展是通过代数的发展完成的，代数这个名字来自阿拉伯数学家 Muhammad ibn Musa al-Khwarizmi，或者更准确地说，他的著作《代数与比较之书》（Kitab al-jabr wa al-muqabalah），其中“al-jabr”一词是现代“algebra”（代数）一词的词源。“Al-jabr”意为“恢复”或“完成”，这对于它所带来的数学发展的重要性来说非常贴切。他的著作并没有包含新的突破性材料；相反，真正天才之处在于对二次方程解法的系统处理。然而，二次方程的完整解集直到十二世纪在西班牙才传入欧洲。

然而，在计算机上实现二次公式并不像最初想象的那么直接。我们假设方程形式为

 

解是众所周知的公式，我当然是指这个公式：

然而，如果你真的将这个公式这样实现到计算机中，那将是自找麻烦。原因是，如果系数 *a* 或 *c* 非常接近于零，可能会导致巨大的截断误差。在计算机上找到根的正确实现方法是

 

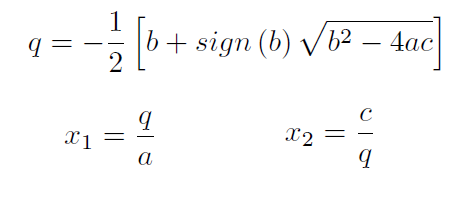
即使系数是复数，计算机公式仍然适用，尽管需要考虑如何取平方根的符号

 

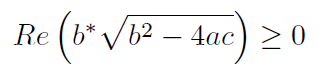
在上面的公式中，Re 代表解的实部，星号代表复数的复共轭。

 

 

三阶和四阶多项式方程

这通常被称为三次或四次方程或函数，毫不奇怪，当我们想计算某个体积时会出现。实际的通用方程直到十六世纪才被解出，尽管巴比伦人解出了一些特殊情况，十二世纪波斯诗人 Omar Khayyam 也给出了一些。然而，并没有迫切需要求解三次方程。没有人等待它被发现，它更多的是一种智力挑战，类似于数学界的奥林匹克运动会，将决定那个时代最伟大的智者。


三次方程的部分解法最早来自目前仍在开放的最古老的大学——博洛尼亚大学，该大学自 1088 年成立以来一直开放。在 1501 年遇到一个涉及三次多项式方程的问题后，Scipione del Ferro 决定着手解决。大约在 1515 年，他找到了一种求解形如 x3+mx = n 的三次方程的方法。Del Ferro 没有发表他的结果，这在当时不幸是很普遍的，只在他临终时告诉了他的学生 Antonio Fiore 和女婿关于他的发现。Fiore 似乎认为这个公式可以随他意愿使用，但他没有立即发表，而是等待时机出现。


因此，当 Niccolò Tartaglia 在 1530 年宣布他可以解决一些关于三次方程的问题时，Fiore 认为他的时机已经到来，并向 Tartaglia 发起了数学辩论。每位参赛者将向对方给出 30 个问题，输家将向赢家支付一笔金钱。他们每个人都有四到五十天的时间来解决这些问题。


当问题交给 Tartaglia 时，他在两个小时内解决了所有问题！而 Fiore 没有解决任何一个给他的问题，他也不知道形如 x3 + mx2 = n 的方程，所以 Tartaglia 赢得了比赛。


1539 年，在一次大规模的保存活动后，一个名叫 Gerolamo Cardano 的人物（他学生时期靠赌博赚钱，并且以粗鲁无礼著称）设法说服 Tartaglia 透露了公式，条件是 Cardano 不会泄露它。然而，Cardano 从 del Ferro 的女婿那里得知了 del Ferro 的解决方案，并决定他不受与 Tartaglia 的协议约束，因为他将发表 del Ferro 的解决方案而不是 Tartaglia 的解决方案，所以他在他的著作《Ars Magna》中发表了结果。这本书被许多当代数学家认为是现代代数的开端，它包含了复数解，尽管 Cardano 对此理解并不深入，因为 Tartaglia 的一些解决方案涉及负数的平方根。（Rafael Bombelli 通常被认为是复数的发现者，因为他对该主题进行了更深入的研究。）这本书出版后，Tartaglia 立即向 Cardano 发起挑战，而 Cardano 在 Tartaglia 的标准看来是一位相当差的数学家，他当即拒绝了。然而，Cardano 的学生 Lodovico Ferrari 向 Tartaglia 发出了无数公开挑战，Tartaglia 都拒绝了。最终，Tartaglia 被提供了一个大学职位，前提是他必须在与 Ferrari 的辩论中获胜。Ferrari 发现了一种求解三次方程的通用方法，这在 Tartaglia 之前是未知的，他早在 1540 年就找到了四次方程的解法，但这需要求解三次方程，所以直到 Cardano 得知 del Ferro 的解决方案后才发表。


Ferrari 赢得了与 Tartaglia 的辩论，Tartaglia 在辩论开始第一天结束前就离开了。（Ferrari 是个相当有意思的人，他十七岁时在一场斗殴中失去了右手所有手指。）此后他的事业飞黄腾达，尽管据称他后来被他姐姐毒害而死。

正如你所理解的，三次方程公式的真正发现者相当复杂，尽管四次方程的解法似乎是 Ferrari 的单独工作。

这些公式通常不在计算机上实现，因为数值技术找到的解几乎总是比它们更好。如果你仍想使用显式公式，你应该实现 Viete 公式，它使用三角函数而不是 Ferrari 的解。

更高次的と言う多项式方程

在求解了二次方程之后，许多人试图求解五次多项式方程，但都失败了。直到 1823 年 Abel 给出了一般证明，说明实际上不可能做到。该定理今天被称为 Abel–Ruffini 定理或 Abel 不可能性定理。之所以有两个名字，是因为 Ruffini 在 1799 年给出了一个不完整的证明，Abel 直到 1826 年才知道。在阅读和研究之后，他说 Ruffini 的工作非常复杂难以理解，他不敢确定是否正确。

然而，了解证明的含义以及它不意味着什么至关重要。Abel 的证明仅说明，无法通过代数方法找到所有五次或更高次多项式方程的通用解。Abel 使用了欧拉积分的推广来证明它，德国数学家 Jacobi 对这一发现未被数学界注意到感到非常惊讶。

然而，可以通过数值方法（牛顿-拉夫逊法）或椭圆积分找到五次方程的解。如果使用 Évariste Galois 理论，还可以找出将找到哪种类型的解。Évariste Galois 也独立于 Abel 和 Ruffini 的工作证明了五次多项式方程无法求解，他的证明于 1846 年在他去世后发表。

显式公式的问题

显式公式存在一些问题，这些问题与计算机的有限存储空间有关，在某些情况下会导致计算出的解与真实值相差甚远。实际上，三次及以上方程的解几乎总是 Jenkins-Traub 算法或其他类似技术的解比显式公式计算出的解更好。

然而，多项式数值估计也存在问题，任何对它们背后算法有足够理解的人都可以轻松构造一个无法收敛的例子。以方程 (1) 为例：

鉴于它是一个五次多项式，只能使用数值算法找到解，但根据代数基本定理，我们知道该方程将有五个实解或复解，正如 Gauss 等人所证明的那样。方程 1 的精确解是： 这个例子的问题在于，C# 和 VB 中实现的Jenkins-Traub 算法无法收敛（最可能是由于用于数据存储的双精度，以及从 VC++ 的 float 库“导出”的 epsilon、min 和 max 值）。事实上，对于这种算法来说，考虑到多个根的数量，总是可能存在收敛问题。原因是该算法从原始方程中提取找到的根，并且如果数值误差过大，可能导致找不到其他解。因此，请注意，任何使用牛顿型迭代的方法都可能在处理多个根时遇到问题。这也适用于根彼此靠近（或相距甚远）的情况。

Jenkins-Traub 确实使用牛顿型方法来查找根，这可能还会导致其他问题。如果一个没有线性项的多项式在零处为零，则迭代技术将无法收敛，因为函数及其导数在零处都为零。

关于具有重根的多项式，还有另一个相当令人惊讶的事情：导数多项式将具有比原多项式少一个相同的根。以方程 1 为例，如果我们对该方程求导，我们将得到

 

当我们尝试使用与之前相同的 Jenkins-Traub 算法来求解这个方程时，我们发现相同的根确实仍然存在，另外还有一个不存在的根。可以通过将值代入原始方程 (1) 来轻松检查解。

实际代码已经变得非常复杂，以至于很难甚至不可能全部解释。我将引导你参考 Wikipedia 上描述的 Jenkins-Traub 过程。

然而，重要的是要知道 Jenkins-Traub 算法被认为是数值计算多项式根的实际标准方法。它经过广泛测试，并且已实现于许多商业产品中（例如 Mathematica 等）。

至于显式公式，它们应该谨慎使用，不能假设它们对你输入的任何实系数都能给出正确结果，尽管程序中的描述应该指明它是否为公认类型，并且输出描述是否与计算出的根匹配。使用了多种不同的方法来查找根，其中包括 Ferrari 方程、标准双二次方程等。

参考

Wolfram 网站提供了使用的一些公式，以及有关所使用的数值算法的其他链接

 

C++ 源代码：

书籍：

其他链接：

© . All rights reserved.