使用正交线性回归对图像中的直线进行拟合

• 下载演示项目 - 11 KB
• 下载源代码 - 29 KB

引言

我最近在做一个项目，需要从图像中识别（曲线）线条，然后将这些线条表示为（直线）线段列表。本文是该代码的一个简化版本，旨在阐述图像中拟合直线的基本原理。

背景

将直线拟合到点集上是一个具有悠久数学历史的复杂问题。在本文中，点意味着像素。但点也可以是科学实验获得的数据。在这两种情况下，我们有时都想找到一条（曲线或直线）能够尽可能精确地拟合这些点。将曲线拟合到一组点上比拟合直线要困难得多。它几乎肯定是迭代的。并且它过于复杂，不适合本文。因此，我们将只关注将直线拟合到一组点上。另外，如果我们需要拟合曲线，我们可以通过在图像的小窗口上应用此算法并存储曲线作为线段列表来完成。为了保持简单，本文将假定我们只需要识别一条直线。现在我们已经定义了问题，我们需要找到一个合适的解决方案。在这种情况下，我们将使用*正交线性回归*。

线性回归

线性回归更常与科学实验联系在一起。通常在实验中，你会得到一组输入数据对应的输出数据。如果幸运的话，输入数据和输出数据之间会存在线性关系。例如，我们可以给电阻施加电压并测量通过它的电流（好吧，这不是一个很令人兴奋的实验！）。我们的数据可能看起来像这样：

电压 (V)	电流 (I)
1.0	0.20
1.5	0.29
2.0	0.44
3.0	0.62
4.0	0.77

我们可以绘制这张图，并使用任何电子表格软件找到穿过点的直线。它看起来像这样：

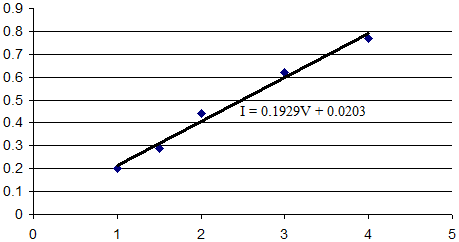
电子表格通常使用线性回归来计算直线趋势线。该直线的方程显示在图表上。

我们必须谨慎解释结果。在本例中，因为我们知道这是一个电阻器，所以 V=0 时的电流应为 0，因此我们可以相当确定截距应为 0，而不是 0.0203。但还有一个更微妙的问题。我们可能会想翻转表格（和图表），以便将电压表示为相对于电流：

电流 (I)	电压 (V)
0.20	1.0
0.29	1.5
0.44	2.0
0.62	3.0
0.77	4.0

如果我们绘制这张图，我们会得到：

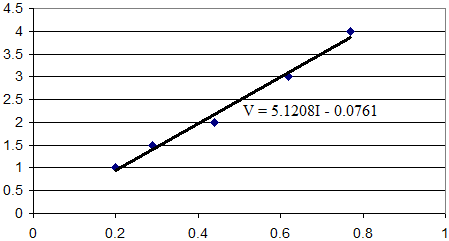
现在我们可以取这条直线的方程并重新排列，以 V 的函数形式得到 I。如果我们这样做，我们会得到：

I = 0.1953V + 0.0149

将此与我们的第一张图进行比较，我们可以看到方程略有不同。为什么？因为标准线性回归假设只有其中一个变量（在本例中是电流）存在误差。而科学实验通常是这样进行的——我们有一个变量是可控的，另一个变量是被测量的。当我们翻转表格/图表时，我们实际上是在说电流是我们选择的变量，而电压是被测量的。这并不是我们实际所做的（实际上我们也没有做第一个实验——我只是编造了数字！但原理是有效的）。

那么这与我们寻找穿过一组点的直线的 问题有什么关系呢？在图像中，我们不能说一个轴是给定的，另一个是被测量的——两个轴都存在误差。所以当我们研究数学时，我们会发现上面使用的标准线性回归不起作用。我们必须使用另一种称为“变量误差”（EIV）线性回归的线性回归。这是一个更复杂的问题，而且目前还不容易解决。因此，我们需要做出一个额外的假设——两个变量中的误差是相同的。这一点很重要，而且是正确的，因为 X 和 Y 是以相同的单位（像素）测量的。另一个重要的观察是，我们试图最小化的误差垂直于我们试图拟合的直线。在标准线性回归中，误差垂直于 x 轴。因此，我们选择正交线性回归。

公式

公式的推导相当复杂，并且在许多论文中都有涵盖，因此我在这里不详细介绍。我将只呈现最终解决方案。

下面的方程将一组像素的坐标作为 (x,y) 对，并找到一条拟合这些点的直线（n = 点数）。这条直线的方程将是 y = a + bx，其中 a 是截距，b 是斜率。作为计算的一部分，我们必须计算以下变量：

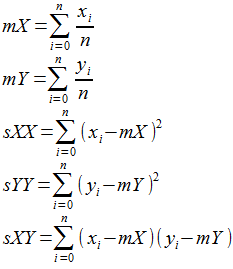
然后我们将它们代入以下方程：

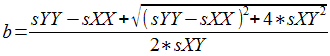
现在我们有了 `b`，我们可以使用以下公式计算 `a`：

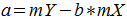
当 `sXY` 不等于零时，上述方程才有效。如果 `sXY` 为零，则有三种可能性：

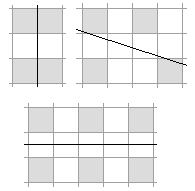
1. 我们得到一条垂直线。当 `sXX` < `sYY` 时，就是这种情况。
2. 我们得到一条水平线。当 `sXX` > `sYY` 时，就是这种情况。
3. 直线不确定。当 `sXX` == `sYY` 时，就是这种情况。

垂直线和水平线是不言自明的。最简单的“不确定线”是一个像素。显然，直线穿过像素的中心，但无法确定直线的方向。其他像素组合（例如，紧密排列的 4 个像素）也将具有此属性。请注意，仅仅因为我们可以确定一条直线，并不意味着我们得到了一条好的直线。一些好的直线示例：

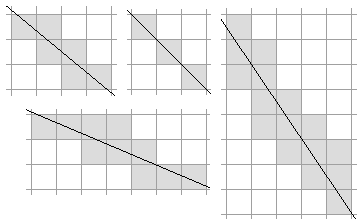
一些不好的直线示例：

我们可以确定直线是否拟合良好的方法。这超出了本文的范围。相反，我们将假设将合理的像素排列传递给线性回归方法。有助于此的一种方法是仅使用与其他像素相邻的像素。这也是一个合理的想法，因为孤立的像素会“拖拽”直线偏离其应有的位置。这是因为我们使用“最小二乘法”来最小化误差。虽然可以使用其他方法，但最小二乘法可确保算法非常稳健。

直线方程

我们可以用多种方式表示直线。直到 20 世纪 80 年代，斜率/截距形式非常普遍。即使现在，它也经常教给学生。这可能是因为它易于可视化。但它有一个严重的限制——它不适用于垂直线。因此，一种更常用的形式是 Ax + By = C。它适用于所有直线。一个小的问​​题是，每条直线都有无限多个 A、B 和 C 值（例如，2x + 3y = 5 与 4x + 6y = 10 是同一条直线）。因此，我们无法直接比较直线。我们可以采取各种方法来*归一化*直线方程，这也能确保系数不会变成非常大或非常小的数字。我们将使用的归一化是确保 C 为正，并且 A² + B² = 1.0。

代码

我已将整个程序实现为 WinForms 应用程序。由于本文的重点是正交线性回归计算，因此它被放在一个单独的库中——`Regression`。像素通过 `IPixelGrid` 接口传递给回归方法，该接口提供了一种简单的方法来访问单个像素。`CalculateLineEquation` 方法以像素网格作为输入。其他输入参数是起始点（`x` 和 `y`）以及要使用的 `width` 和 `height`。该方法返回三个直线方程系数：`a`、`b` 和 `c`。

public static void CalculateLineEquation(IPixelGrid grid, int x, int y, int width, int height,
                                         out float a, out float b, out float c)
{
    a = 0.0f;
    b = 0.0f;
    c = 0.0f;

    int n = 0, sX = 0, sY = 0;
    double mX, mY, sXX = 0.0, sXY = 0.0, sYY = 0.0;

    //Calculate sums of X and Y
    for (int iy = y; iy < y + height; iy++)
    {
        for (int ix = x; ix < x + width; ix++)
        {
            if (grid.GetPixel(ix, iy))
            {
                n++;
                sX += ix;
                sY += iy;
            }
        }
    }

    //Calculate X and Y means (sample means)
    mX = (double)sX / n;
    mY = (double)sY / n;

    //Calculate sum of X squared, sum of Y squared and sum of X * Y
    //(components of the scatter matrix)
    for (int iy = y; iy < y + height; iy++)
    {
        for (int ix = x; ix < x + width; ix++)
        {
            if (grid.GetPixel(ix, iy))
            {
                sXX += ((double)ix - mX) * ((double)ix - mX);
                sXY += ((double)ix - mX) * ((double)iy - mY);
                sYY += ((double)iy - mY) * ((double)iy - mY);
            }
        }
    }

    bool isVertical = sXY == 0 && sXX < sYY;
    bool isHorizontal = sXY == 0 && sXX > sYY;
    bool isIndeterminate = sXY == 0 && sXX == sYY;
    double slope = double.NaN;
    double intercept = double.NaN;

    if (isVertical)
    {
        a = 1.0f;
        b = 0.0f;
        c = (float)mX;
    }
    else if (isHorizontal)
    {
        a = 0.0f;
        b = 1.0f;
        c = (float)mY;
    }
    else if (isIndeterminate)
    {
        a = float.NaN;
        b = float.NaN;
        c = float.NaN;
    }
    else
    {
        slope = (sYY - sXX + Math.Sqrt((sYY - sXX) * (sYY - sXX) + 4.0 * sXY * sXY)) / (2.0 * sXY);
        intercept = mY - slope * mX;
        double normFactor = (intercept >= 0.0 ? 1.0 : -1.0) * Math.Sqrt(slope * slope + 1.0);
        a = (float)(-slope / normFactor);
        b = (float)(1.0 / normFactor);
        c = (float)(intercept / normFactor);
    }
}

主窗体（`MainForm`）有一个用户控件（`PixelGridUserControl`）来显示像素，并允许用户打开或关闭像素。一旦我们计算出直线（以 Ax+By=C 的形式），我们就可以调用 `DrawLine` 方法来显示它。请注意，由于我们将像素显示为大正方形（且像素中心是正方形的中心），因此显示网格的边缘实际上比预期的要多半个像素。因此，显示的原点实际上是 (-0.5,-0.5)，例如（当我们稍后绘制这条直线时，我们必须计算每个像素的正方形大小——并且会根据我们调整窗体大小的程度而变化）。

注意：如果您想使显示的像素网格变大或变小，`PixelGridUserControl` 中有一个常量 `NUM_PIXELS`。默认设置为 10，但可以在 2 到 500 之间（尽管我不建议超过 50！——我没有尝试使其适用于大型网格）。

还有一个测试库。默认情况下，它不包含在构建中。如果使用，需要安装 NUnit 2.6。

兴趣点

该算法几乎肯定会成为一个更大解决方案的一部分。通常，图像首先需要经过处理以提取线条或边缘。初始处理的类型将非常依赖于应用程序。

一旦有了线条，您通常需要对这些线条使用几何例程，例如计算线条的交点、线条之间的角度、确定形状等。如果本文引起足够的兴趣，我可能会撰写后续文章，展示如何实现一些几何计算。

参考文献 

• 线性回归（维基百科）
• 圆和直线回归：最小二乘法拟合圆和直线（Nikolai Chernov）

历史

• 2013年4月11日：初始版本。