DotNetMatrix：.NET 平台的简单矩阵库

• 下载源代码、示例项目和 HTMLHelp 文档 - 106.3 KB

引言

本文提供的类集为您提供了一个基本的 .NET 线性代数包。它提供了用于构造和操作实数、稠密矩阵的用户级 C# 类。其目的是提供足够的功能来处理常规问题，并以一种对非专家而言自然且易于理解的方式进行打包。也就是说，它只是一个公共域 Java 矩阵库 JAMA 的移植。有关更多信息，请查看 JAMA 网站。

背景

目前，我在日本一家小型 GIS 公司工作，为应用程序开发者开发 GIS 组件。坐标变换（因此也包括仿射变换）是我们开发工作的一个基本组成部分。最近，我被指派设计和实现一个用于 .NET 框架的新 GIS 系统，该系统能够轻松移植到 Java 和其他框架。我决定最大程度地利用基于矩阵的仿射变换，这也是 OpenGIS 坐标变换规范的要求。

然后，我发现 .NET 中的 GDI+ 部分提供的 Matrix 类实现的仿射变换方式与标准规范不同。简而言之，虽然标准的 2D 坐标系仿射变换矩阵定义为

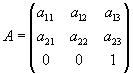
GDI+ 定义的矩阵是

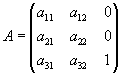
其结果是，使用 GDI+ Matrix 类的大多数仿射变换将不符合标准或规范。例如，按照标准（和数学上）的定义，逆时针（或反时针）旋转被视为正数，但在使用 GDI+ 类时必须是负数。
为了解决这个问题，我决定实现一个标准的仿射变换矩阵，并找到了这个小型的 Java 通用矩阵库 - JAMA。本文提供的类是从 JAMA 移植过来的，并添加了 .NET 特定的改进，例如运算符重载等。

在另一篇文章中，我将讨论并介绍我的仿射变换矩阵，它应该能产生相同的效果（与 GDI+ Matrix 类具有相同的属性和方法）。本文的其余部分摘自 JAMA 文档，我将把该库称为 **DotNetMatrix**（命名空间）。

功能

DotNetMatrix 由六个 C# 类组成：GeneralMatrix、CholeskyDecomposition、LUDecomposition、QRDecomposition、SingularValueDecomposition 和 EigenvalueDecomposition。

GeneralMatrix 类提供了数值线性代数的基本运算。各种构造函数可以从双精度浮点数二维数组创建矩阵。各种 get 和 set（属性）提供对子矩阵和矩阵元素的访问。基本算术运算包括矩阵加法和乘法、矩阵范数以及选定的逐元素数组运算。还包含一个方便的矩阵打印方法。

五个基本的矩阵分解（包括一对或三对矩阵、排列向量等）会在五个分解类中产生结果。GeneralMatrix 类通过这些分解来计算线性方程组解、行列式、逆矩阵和其他矩阵函数。这五种分解是：

• 对称正定矩阵的 Cholesky 分解
• 任意矩形矩阵的 LU 分解（高斯消元）
• 任意矩形矩阵的 QR 分解
• 对称和非对称方阵的特征值分解
• 任意矩形矩阵的奇异值分解

DotNetMatrix 只处理实数矩阵，不支持复数矩阵。

DotNetMatrix 的设计是为了在纯粹优雅的面向对象设计需求与实现高性能的需求之间取得平衡。

DotNetMatrix 功能概述

对象操作	构造函数 设置元素 获取元素 复制 clone
基本运算	加法 减法 乘法 标量乘法 逐元素乘法 逐元素除法 一元负号 转置 范数
分解	Cholesky LU 二维码 SVD 对称特征值 非对称特征值
方程求解	非奇异系统 最小二乘
派生量	条件数 行列式 秩 逆矩阵 伪逆

Using the Code

下面是一个简单的例子，用于求解 3x3 线性系统 Ax=b 并计算残差的范数。

double[][] array = {{1.,2.,3},{4.,5.,6.},{7.,8.,10.}};
GeneralMatrix A = new GeneralMatrix(array);
GeneralMatrix b = GeneralMatrix.Random(3,1);
GeneralMatrix x = A.Solve(b);
GeneralMatrix Residual = A.Multiply(x).Subtract(b);
double rnorm = Residual.NormInf();

关注点

所有类中都有一个空的 ISerializable 接口实现。我不知道是否真的需要序列化支持，如果需要，我可以完成这些实现。

许可证

这基本上是公共域代码的移植，因此结果也属于公共域。

历史

• 2004 年 1 月 10 日 - 首次发布

结论

矩阵是宝贵的数学工具，可以用来解决非常复杂的问题，坐标变换也不例外。本文提供的类集可以帮助您实现自己的仿射变换类，以实现 .NET 框架所能提供的更多功能。此外，由于这些类完全是用 C# 编写的，与 .NET 框架中的 GDI+ 类（它们是 COM 实现的包装器）不同，因此没有互操作开销。

在我的下一篇文章中，我将介绍一个基于此库的仿射变换矩阵类。欢迎提出改进建议。