高精度本机高斯消元法

Kenneth Haugland

4.91/5 (18投票s)

2013年7月5日

CPOL

12分钟阅读

72148

2358

使用高斯消元法求解线性方程组和求逆矩阵。

介绍

高斯消元法是一种常用于求解线性方程组的技术，因为它是一种非常稳定的求解方法。网上有很多例子展示了如何求解，但很少能很好地解释它们为什么有效以及潜在的问题，特别是潜在的舍入误差。关键在于理解高斯消元法和矩阵求逆的计算原理，一旦理解了，求解方程就会变得非常简单。这两种计算方法将为您提供一个通用的工具箱，可用于许多重要应用，例如样条计算、多项式拟合等。

背景

一组线性方程组可以通过高斯消元法来求解，这时我们需要方程的变量数量与方程数量相等才能求解，可以表示为：

然而，为了求解这些方程，我将采用将方程写成矩阵形式的方法。

为了求解方程组中的未知数，我们要将方程左侧转化为单位矩阵，右侧得到解，如下所示：

最左边的矩阵，对角线上为1，其余为0，称为单位矩阵。如果您还记得早期数学课上的内容，您会注意到矩阵的行数和列数是相同的，这意味着您需要X个方程来求解X个未知数。还有一个概念是，当左边的两个矩阵相乘时，我们会得到以下值，以及方程的解：

从这些信息我们可以立即得出，来自三个原始方程的对角线上的值不能为零。在我们的例子中，这意味着第一个方程中的x不能为零，第二个方程中的y不能为零，第三个方程中的z不能为零。如果它们为零，我们将不得不重新排列方程，使其不为零，例如将方程一与方程二交换等，而不违反对角线不能为零的第一个条件。

此处示例中的方程不需要重新排列，因为它们不违反条件，所以我们开始构建单位矩阵，方法是将第一个方程除以2，这将使我们所寻求的对角矩阵的第一个1生成。

下一步是消除第二个方程中的x值，方法是将第一个方程乘以3后加到第二个方程上。

现在第二个方程的x值为零，这也必须对第三个方程进行，方法是将第一个方程乘以2后加到第三个方程上。

为了在第二个方程中形成单位矩阵，我们需要将其乘以2。

为了形成最后一个零，我们需要消除第三个方程中的y值，这只需将第二个方程乘以2后减去即可。

现在需要将最后一个方程乘以-1，我们得到z值的解z=-1。

这就完成了所谓的“前向替换”，因为矩阵的对角线以下的元素都为零。现在是时候开始所谓的“后向消元”了。从消除第一个方程中的y值开始，这只需将第二个方程乘以1/2后减去即可。

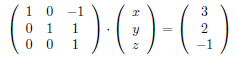
现在，通过将第一个方程加上第三个方程，来消除第一个方程中的z值。

最后，将第二个方程乘以-1后减去第三个方程，我们得到：

这样我们就得到了解，当然是x=2, y=3, z = -1。这是高斯消元法过程的一个非常详细的讲解，您可以理解，无论有多少变量，这都可以自动完成。值得一提的是，我们也可以随时手动完成。

代码中的高斯消元法

现在我们继续在代码中实现前向消元。我们将完全跳过第一行，这意味着在实现前向高斯消元时，第一个方程保持不变。

首先，我们将第二个方程（或后面的值）除以第一个方程的x值以及x的值，或者更确切地说，总是当前单位矩阵中的实际值。下面的代码描述了矩阵名为a，右侧向量名为b的实现。

重要的是要注意，这将把单位矩阵下方的所有值设置为零。这实际上也将给出最后一个值的解，在上一节给出的示例中，就是z的值。根据这些信息，我们现在可以计算所有变量，原因是最后一个方程解出了最后一个变量，下一个方程有一个未知数需要确定，因为我们可以将最后一个值代入其中，以此类推。

Public Function GaussElimination(ByVal ResultingVector As Matrix) As Matrix

    ' Check that both the matrix dimensions are correct 
    If Not (Me.Cols = ResultingVector.Rows And ResultingVector.Cols = 1) Then
        If Me.Cols <> ResultingVector.Rows And ResultingVector.Cols <> 1 Then
            Throw New Exception("The number of columns (variables) is different " & _ 
              "form the number rows (number of equations), " & _ 
              "and there is too many columns in the ResultingVector matrix.")
        ElseIf Me.Cols <> ResultingVector.Rows Then
            Throw New Exception("The number of columns (variables) is different " & _ 
              "form the number rows (number of equations).")
        ElseIf ResultingVector.Cols <> 1 Then
            Throw New Exception("There is too many columns in the ResultingVector matrix.")
        End If
    End If

    Dim a As New Matrix(Rows, Cols)

    For i As Integer = 0 To Rows - 1
        For j As Integer = 0 To Cols - 1
            a.Item(i, j) = Me.Item(i, j)
        Next
    Next
    Dim result, b As New Matrix(Rows, 1)
    For i As Integer = 0 To Rows - 1
        b.Item(i, 0) = ResultingVector(i, 0)
    Next

    Dim m, Sum As Double

    For k As Integer = 0 To Rows - 2
        For i As Integer = k + 1 To Rows - 1
            m = a.Item(i, k) / a.Item(k, k)
            For j As Integer = 0 To Cols - 1
                a(i, j) -= m * a.Item(k, j)
            Next
            b(i, 0) = b(i, 0) - m * b(k, 0)
        Next
    Next

    For i As Integer = Rows - 1 To 0 Step -1

        Sum = 0
        result(i, 0) = 0
        For k As Integer = i + 1 To Rows - 1
            Sum += a(i, k) * result(k, 0)
        Next
        result(i, 0) = (b(i, 0) - Sum) / a(i, i)
    Next

    Return result
End Function

这些值现在存储在结果向量中，这就完成了高斯消元。

高斯消元法的问题

高斯消元法几乎从不直接实现，就像在前几节的代码片段中所见的那样，因为方程的矩阵在计算之前可能在单位矩阵中出现零，并且在减去前一个方程时也可能在单位矩阵中出现零。这两个问题都可以通过“主元法”来解决，这意味着重新排列矩阵中的方程顺序，以避免问题的发生。重要的是要注意，在每次迭代中，当我们用一个方程减去另一个方程时，都可能出现零的问题，如下例所示：

我们将第二行方程减去第一行的一半，得到：

实际上，单位矩阵中出现零的可能性问题与高斯消元法的第二个问题，即解的精度问题，是相关的。我们可以用一个例子来演示这一点：

即使使用双精度，我们也无法获得精确值（x=1, y=1, z=1），高斯消元法在计算中对数字位数有极高的要求。这可以通过使用System.Numerics.BigInteger类而不是Decimal或Double进行分数计算来解决，这样可以消除计算误差，即使对于相对较小的数字也是如此。我们应该提到，我们可以使用高斯-约旦法，或者更好的高斯-赛德尔迭代法。

然而，在进行主元法对矩阵进行处理时，我们应该记住它实际上是什么。我们可以像前面建议的那样，交换方程的顺序，即交换方程的行。这被称为“部分主元法”，因为我们也可以改变变量的顺序。如果我们交换行和变量，则称为“完全主元法”。假设我们有一个n*n维矩阵的方程组，我们有n!种组织行的方式，如果我们还交换变量，则有n! * n!种。

在进行主元法处理之前，有一个问题是哪种组织方式最可取。通常的方法是取绝对值最大的元素并将其放在矩阵的对角线上，这是为了最小化舍入误差，我将按照这种方式组织矩阵。这也是每个元素将被组织的方式。

排序是通过所谓的“冒泡排序”完成的，这通常是一种效率不高的方法，因为我们只需要第一个元素中的最大值，所以可以搜索最大值然后将其交换为新的顶元素。代码写法如下：

Public Shared Function SortByValue(ByVal A As FractionsMatrix, _
       b As FractionsMatrix, ByVal index As Integer) As Fraction
    Dim n, i As Integer
    n = A.Rows
    i = index
 
    Dim CurrentMaximumValue As Double = 0
 
    Dim j As Integer = index
 
    Do
        If Math.Abs(A(j, index).ToDouble) < Math.Abs(A(j + 1, index).ToDouble) Then
            A.SwapRows(j, j + 1)
            b.SwapRows(j, j + 1)
            j = index
        Else
            j += 1
        End If
 
    Loop Until j = n - 1
 
    Return A(index, index)
 
End Function

它不允许矩阵的每种组合都展开，但对于大多数实际情况已经足够了。

分数类

构建分数类的主要问题是，我们立即遇到从Decimal或Double构建分数的难题。有两种选择，一种是从10进制分数构建。如果是这样，我们则需要小数点后的有效数字位数，这可以通过下面的方法完成，其中“Number*”是“decimal”或“double”。

Dim SignificantDigitCount As Integer = BitConverter.GetBytes(Decimal.GetBits(Number)(3))(2)

这将返回直到其余为零的所有数字的计数，但这不是首选技术。连分数是从十进制数中获取分数的最佳方法，因为它能获得十进制数0.333333333等的精确分数，而这是其他方法无法实现的。对于像pi和e这样的无理数，它也能更快地收敛。然而，在实现时需要注意过早从十进制转换为整数，因为我们很快就会出现舍入误差。构建连分数的代码如下：

Sub New(ByVal Number As Decimal)
 
    Dim ResultingFraction As New Fraction

    Dim k As Double = 1
    If Number < 0 Then
        k = -1
    End If

    ResultingFraction = GetFraction(Math.Abs(Number))
    ResultingFraction.Numerator *= k

    Me.Numerator = ResultingFraction.Numerator
    Me.Denominator = ResultingFraction.Denominator
End Sub

Private Function GetFraction(ByVal d As Decimal)
    Dim Temp As Decimal = d

    Dim list As New List(Of Decimal)

    For i As Integer = 0 To 1000
        list.Add(Math.Truncate(Temp))
        Dim ff As Decimal = GetContinuedFraction(list).ToDouble
        If d = ff Then
            Exit For
        End If
 
        Try
            Temp = 1 / (Temp - Math.Truncate(Temp))
        Catch ex As Exception
            Exit For
        End Try
    Next


    Return GetContinuedFraction(list)
End Function

Private Function GetContinuedFraction(ByVal d As List(Of Decimal)) As Fraction
    Dim result As New Fraction
    result.Numerator = d(d.Count - 1)
    result.Denominator = 1


    For i As Integer = d.Count - 2 To 0 Step -1
        If Not result.Denominator = 0 Then
            result = New Fraction(d(i), 1) + 1 / result
        End If
    Next

    Return result
End Function

分数必须包含两个值，即分子和分母，才能执行计算。但是整数值可能会变得非常大，所以我们需要使用System.Numerics.BigInteger。

分数的计算很简单，我们可以查看代码了解如何进行，但是当我们想将分数转换为double或decimal数时，需要小心。BigInteger类可能包含非常大的值，实际上大到无法直接转换为十进制数值。

如果我们确实想确保这一点，我们应该考虑它，但是double的最大值允许大约307位数字，所以如果得到一个大于这个数字的数，我们就需要采用类似的代码：

Public Function ToDouble() As Double
 
    Dim NumberOfNumeratorDigits, NumberOfDenuminatorDigits, MaximumDoubleDigits As Integer
    NumberOfNumeratorDigits = GetNumberOfDigits(Me.Numerator)
    NumberOfDenuminatorDigits = GetNumberOfDigits(Me.Denumerator)
    MaximumDoubleDigits = CInt(Math.Log10(Double.MaxValue)) - 1

    Dim ResultingDoubleValue As Double

    If MaximumDoubleDigits > NumberOfDenuminatorDigits And _
            MaximumDoubleDigits > NumberOfNumeratorDigits Then
        ResultingDoubleValue = CDbl(Me.Numerator) / CDbl(Me.Denumerator)
    Else
        If MaximumDoubleDigits < NumberOfNumeratorDigits And _
                 MaximumDoubleDigits < NumberOfDenuminatorDigits Then
            Dim Over, Below As Integer
            Over = NumberOfNumeratorDigits - MaximumDoubleDigits
            Below = NumberOfDenuminatorDigits - MaximumDoubleDigits

            Me.Numerator /= 10 ^ Over
            Me.Denumerator /= 10 ^ Below

            ResultingDoubleValue = CDbl(Me.Numerator) / CDbl(Me.Denumerator)
            ResultingDoubleValue *= CDbl(10 ^ (Over - Below))

        ElseIf MaximumDoubleDigits < NumberOfDenuminatorDigits Then
            Dim Below As Integer
            Below = NumberOfDenuminatorDigits - MaximumDoubleDigits
            Me.Denumerator /= 10 ^ Below

            ResultingDoubleValue = CDbl(Me.Numerator) / CDbl(Me.Denumerator)
            ResultingDoubleValue *= CDbl(10 ^ (Below))
        ElseIf MaximumDoubleDigits < NumberOfNumeratorDigits Then
            Dim Over As Integer
            Over = NumberOfNumeratorDigits - MaximumDoubleDigits

            Me.Numerator /= 10 ^ Over
 
            ResultingDoubleValue = CDbl(Me.Numerator) / CDbl(Me.Denumerator)
            ResultingDoubleValue *= CDbl(10 ^ (Over))
        End If
    End If

    Return ResultingDoubleValue
End Function

数字的位数可以通过以下函数找到：

Private Function GetNumberOfDigits(ByVal d As System.Numerics.BigInteger) As Integer
    Dim NumberOfDigits As Integer

    If d < 0 Then
        d *= -1
    End If

    If d = 0 Then
        NumberOfDigits = 1
    Else
        NumberOfDigits = System.Numerics.BigInteger.Log10(d) + 1
    End If
    Return NumberOfDigits
End Function

BigInteger类有一个名为gcd（最大公约数）的函数，可以用来简化分数。如果分数已经是其最短形式，该函数将返回1（但如果分数为(0/0)，它也可以返回0）。

Private Shared Function MinFraction(ByVal FratNumber As Fraction) As Fraction
    Dim CommonDivisor As New System.Numerics.BigInteger

    Do
        CommonDivisor = System.Numerics.BigInteger.GreatestCommonDivisor(_
               FratNumber.Numerator, FratNumber.Denumerator)
        If CommonDivisor = 0 Then Exit Do
        FratNumber.Numerator /= CommonDivisor
        FratNumber.Denumerator /= CommonDivisor
    Loop Until CommonDivisor = 1

    Return FratNumber
End Function

逆矩阵

逆矩阵实际上与求解矩阵相同，但要求它是方形的，并且行列式不为零。获得逆矩阵的步骤，前提是它确实存在，与高斯消元过程几乎完全相同。

我们从开头相同的例子开始，除了不包含常数，矩阵写成如下形式：

我们现在想要做的是，对等式两边的每一行进行乘、加或减运算，以便在左侧创建一个单位矩阵，并在右侧得到逆矩阵。

然而，与高斯消元法一样，单位矩阵中的零仍然是一个问题，需要通过主元法解决。这可以通过将单位矩阵分成三部分，然后使用普通高斯消元法求解每一列，并在之后将它们重新排列成单位矩阵来完成。

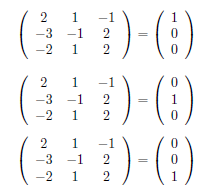
当然，这个过程可以自动化，并且会包含逆矩阵的每一列可以像这样写在代码中：

Public Function Inverse() As Matrix
    Dim result As New Matrix(Rows, Cols)

    For i As Integer = 0 To Rows - 1
        Dim v As New Matrix(Rows, 1)
        v(i, 0) = 1

        Dim res As New Matrix
        Dim inputs As New Matrix(Rows, Cols)

        For m As Integer = 0 To Cols - 1
            For l As Integer = 0 To Rows - 1
                inputs(l, m) = Me(l, m)
            Next
        Next

        res = inputs.GaussElimination(v)

        For k As Integer = 0 To Rows - 1
            result(k, i) = res(k, 0)
        Next

    Next

    Return result

End Function

行列式

行列式是任何矩阵库中的一种重要的计算类型，因为它是一个公认的属性，并且有快速且数值稳定的计算方法。这导致了关于行列式的使用及其含义和影响的整本书籍的编写。程序员遇到行列式计算的一个地方是几何测试，其中大多数方程都可以重写以利用计算出的行列式值。

在几何函数中使用它的地方的一些例子是：

点位于哪条线（2D）的一侧（我在这次实现中使用了这个，它也可以用来计算2D凸包）。
点位于哪个三角形（3D）的一侧。
点在圆（2D）内部。
点在球体（3D）内部。
克莱默法则求解方程组。
等等。

我将使用前向替换来计算矩阵的行列式（三种选项之一，另外两种是通过公式或通过使用余子式和代数余子式），但是为了做到这一点，必须看一下行列式的性质。一些最重要的性质是：

如果矩阵被转置，其行列式保持不变|A| = |A^T|。
如果交换两个行或两个列，行列式会改变符号，从|A|变为-|A|。
如果一行或一列只有零，则行列式也为零。

行列式是使用前向替换计算的，即与原生高斯消元法相同，因此在计算行列式时必须应用上述规则，特别是当两个列或行互换时改变符号非常重要。必须提前检查最后一个条件，即一行或一列的所有值为零（这意味着行列式将为零），因为在此配置下计算可能会得到NaN作为结果。

完成前向替换后，就剩下一个三角矩阵，其行列式就是主对角线元素的乘积。代码如下：

  Private Shared DeterminantSign As Integer = 1

    Public Function Det() As Double

        DeterminantSign = 1

        'Check that both the matrix dimensions are correct 
        If Not (Me.Cols = Me.Rows) Then
            Throw New Exception("The number of columns (variables) is different form the number rows (number of equations), and there is too many columns in the ResultingVector matrix.")
        End If

        Dim a As New FractionsMatrix(Rows, Cols)

        'Order the original equation set from 
        'the highest to lowest according to their unity value
        For i As Integer = 0 To Me.Rows - 2
            SortByValue(Me, i)
        Next

        For i As Integer = 0 To Rows - 1
            For j As Integer = 0 To Cols - 1
                a.Item(i, j) = Me.Item(i, j)
            Next
        Next

        Dim m, Sum As New Fraction

        Dim HitZero As Boolean = False

        'Forward elimination
        For f As Integer = 0 To Rows - 1
            If f <> 0 Then
                For i As Integer = 0 To Rows - 1
                    For j As Integer = 0 To Cols - 1
                        a.Item(i, j) = (Me.Item(i, j))
                    Next
                Next

                DeterminantSign *= -1
                a.SwapRows(0, f)
                HitZero = False
            End If

            For k As Integer = 0 To Rows - 2
                For i As Integer = k + 1 To Rows - 1
                    m = a.Item(i, k) / a.Item(k, k)
                    For j As Integer = 0 To Rows - 1
                        a(i, j) -= m * a.Item(k, j)
                    Next
                Next

                'Check for zeroes here as there is no need to 
                If FractionsMatrix.SortByValue(a, k).ToDouble = 0 Then
                    HitZero = True
                    Exit For
                End If
            Next

            ' No zeroes found; resume to backward substitution
            If HitZero = False Then
                Exit For
            End If
        Next

        Dim result As New Fraction(1, 1)

        'Calculate the diagonal product
        For i As Integer = 0 To Me.Cols - 1
            result *= a.Item(i, i)
        Next

        'Return the diagonal product multiplyed by the changing sign given by row swaps
        Return result.ToDouble * DeterminantSign
    End Function

现在唯一缺少的是检查被零填满的行和列，如下面的代码所示：

     ''' <summary>
    ''' Check for row or colums containing nothing but zeroes
    ''' </summary>
    ''' <param name="a"></param>
    ''' <returns></returns>
    ''' <remarks></remarks>
    Public Function IsDetermenantZero(ByVal a As FractionsMatrix) As Boolean
        Dim result As Boolean = True

        For i As Integer = 0 To a.Cols - 1
            result = True
            For j As Integer = 0 To a.Rows - 1
                If a.Item(j, i).todouble <> 0 Then
                    result = False
                End If
            Next
            If result Then
                Return True
            End If
        Next

        For i As Integer = 0 To a.Rows - 1
            result = True
            For j As Integer = 0 To a.Cols - 1
                If a.Item(i, j).todouble <> 0 Then
                    result = False
                End If
            Next
            If result Then
                Return True
            End If
        Next

        Return result
    End Function

这结束了行列式的计算。

历史

2013年8月26日 - 添加了行列式计算。

参考文献

Shaharuddin Salleh等著《Visual C++ .NET数值模拟与案例研究》。
Jack Xu著《C#实用数值方法》。
John C. Davis著《地质学统计与数据分析（第三版）》。
William Press等著《C++数值计算（第二版）》。
Christer Ericson著《实时碰撞检测 - 交互式3D技术系列》。