使用 OpenGL 进行线性刚体动力学模拟

引言

要真实地动画3D模型，理解动力学原理至关重要，动力学描述了现实世界中物体的运动。计算物理学已在游戏和模拟工具中变得司空见惯，本文解释了如何将线性动力学与OpenGL渲染相结合。

自牛顿时代以来，科学家和工程师就已理解了动力学定律，程序员也对利用这些原理在3D环境中动画物体越来越感兴趣。如果你在网上搜索，会找到大量相关材料。我特别推荐Chris Hecker的文章以及Andrew Witkin、David Baraff和Michael Kass编写的讲义。

许多资料讨论了动力学背后的理论，有些还展示了如何在代码中实现这些方程。但本文更进一步，展示了如何在基于OpenGL的实际应用中实现刚体动力学。这个应用程序的代码可以在这里获取，它为球体分配了速度和加速度，然后渲染球体在空间中移动的路径。图1展示了这在我的Linux系统上的样子。

 

  

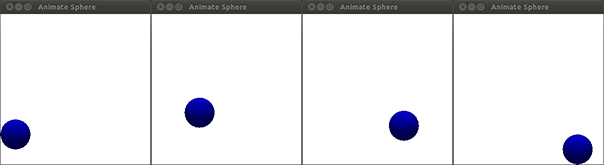
图1：受线性动力学作用的球体运动

这可能看起来不那么令人印象深刻，但代码背后的方法可以扩展到更复杂的情况。但在我讨论代码之前，我需要介绍线性动力学的基础理论。第一节将详细讨论这一点。

注意：本文只关注线性动力学，不讨论旋转动力学。此外，本文只讨论差分方程，不讨论微分方程或积分方程。

1. 线性动力学基础

在许多电子游戏中，物体似乎总是以相同的速度移动。但在现实世界中，物体的速度会随时间变化，尤其是在重力影响下。为了解释其工作原理，本节首先讨论位置和速度，然后讨论加速度和力的重要概念。

1.1 位置和速度

如果你熟悉图形建模，就会知道一个点的位置是作为一组坐标给出的，这些坐标相对于另一个点（称为原点）来确定其位置。在三维欧几里得空间中，坐标以(x, y, z)三元组的形式给出，其中x表示沿x轴与原点的距离，y表示沿y轴与原点的距离，z表示沿z轴与原点的距离。

区分距离和位置很重要。如果一个点的位置r表示为(x, y, z)，它与原点的距离|r|等于sqrt(x² + y² + z²)。距离标识了一个点有多远，因为它只有一个值，所以称为标量。相反，位置标识了一个点有多远以及它的方向。一个标识大小和方向的量称为向量。

创建动画设计时，仅知道点的位置是不够的。你必须知道它的位置如何从一帧变为下一帧。我们将渲染帧之间的时间间隔称为Δt，以秒为单位。例如，如果应用程序的帧速率是120 fps（每秒帧数），则时间间隔Δt = 1/120 = 0.008333秒。

位置随时间的变化称为速度。如果一个点的位置在时间间隔Δt内变化了(Δx, Δy, Δz)，则该间隔内的平均速度表示为(Δx/Δt, Δy/Δt, Δz/Δt)。为了简化表示，我们将平均速度向量表示为v，其分量将给出为v_x = Δx/Δt，v_y = Δy/Δt，v_z = Δz/Δt。

注意：本讨论仅涉及时间间隔内的平均速度，而不是特定时间点的瞬时速度。这对物理学家来说很重要，但对程序员来说则不然。因此，我将停止使用“时间间隔内的平均速度”这一短语。

在物理学中，速度以米/秒表示。也就是说，如果一个点的速度是(5, 5, 0)，它的位置每秒在+x方向改变五米，在+y方向改变五米。程序员不常用米，所以我们将速度表示为通用单位/秒。

假设你知道一个点的速度，但不知道它的位置如何从一帧变为下一帧。在这种情况下，以下方程会很有用

这表明，要找到新位置，将旧位置加上速度和时间间隔的乘积。这应该很容易理解。如果你以64英里/小时（103公里/小时）的速度行驶半小时，你将行驶64 × 0.5 = 32英里或103 × 0.5 = 51.5公里。

图2展示了另一个例子。点的初始位置为y₀ = 0.5，它以速度v_y = 1向上移动。每个时间间隔为0.75秒，因此第一个更新位置y₁ = 0.5 + 1(0.75) = 1.25。第二个位置y₂ = 1.25 + 1(0.75) = 2。每个位置都比前一个位置多0.75。

  

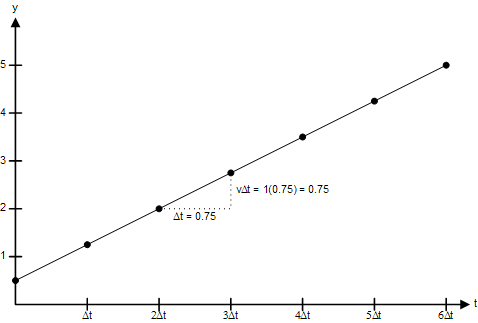
图2：一个点在恒定速度下的轨迹

一个点随时间经过的路径称为它的轨迹，如果速度是恒定的，轨迹将是一条直线。接下来的讨论将探讨当物体的速度随时间变化时会发生什么。

1.2 加速度和力

正如速度衡量位置随时间的变化一样，加速度衡量速度随时间的变化。像位置和速度一样，加速度是一个向量。以下方程显示了它与速度的关系：

 

一个重要问题出现了。我们知道如何在给定速度的情况下更新点的位置，也知道如何在给定加速度的情况下更新速度。但是，如何在给定初始速度和加速度的情况下更新点的位置呢？也就是说，如果知道r_i、v_i和a，如何获得r_i+1？

为了得到答案，请记住速度在时间间隔Δt内从v_i变为v_i+1。该间隔内的平均速度可以如下计算

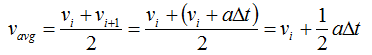
有了这个表达式，我们可以如下确定更新后的位置

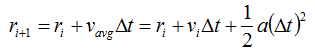
现在让我们看看一个具有恒定加速度的点的轨迹。假设一个点有 r₀ = 0.5，v₀ = 2 和 a = -1。在第一个时间间隔后，更新后的位置 r₁ 等于 0.5 + 2(0.75) + (0.5)(-1)(0.75)² = 1.72。更新后的速度 v₁ 等于 2 + (-1)(0.75) = 1.25。在第二个时间间隔后，r₂ = 1.72 + (1.25)(0.75) + (0.5)(-1)(0.75)² = 2.375，v₂ = 1.25 + (-1)(0.75) = 0.5。

通过跟踪累计时间间隔，我们可以在不计算速度的情况下获得每一步的位置。例如，我们可以通过将方程中的时间间隔设置为2Δt来从r₀前进到r₂。也就是说，r₂ = r₀ + v₀(2Δt) + (0.5)(a)(2Δt)² = 2.375。图3显示了该点从Δt到6Δt的轨迹。

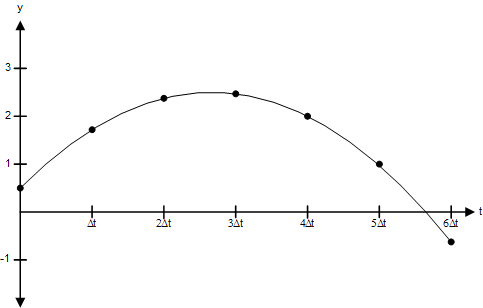
图3：一个点在恒定加速度下的轨迹

如图所示，一个具有初始速度和恒定加速度的点的轨迹是抛物线。这应该很容易理解，因为位置方程是关于时间的二次方程，而二次方程的图形成抛物线。

程序员和工程师通常只关注位置、速度和加速度，而不考虑加速度随时间的变化。这是因为力在物理学中扮演着非常重要的角色——从摩擦力到重力再到电磁力，影响物理运动的现象通常都用力来量化。当力作用于物体并使其移动时，物体的加速度等于力除以物体的质量。用方程表示为 F = ma，其中 F 是牛顿力，m 是千克质量，a 是米/秒²加速度。

至此，你应该对位置、速度和加速度之间的关系有了清晰的理解。这些都以向量形式给出，下一节将展示如何利用它们来约束OpenGL渲染中物体的运动。

2. 线性动力学与OpenGL

现代OpenGL应用程序将顶点位置存储在称为顶点缓冲区对象（VBO）的结构中。随着渲染过程的进行，顶点着色器处理VBO的元素以确定顶点的最终位置。因此，我们将依靠顶点着色器用物理计算的结果来更新VBO数据。

具体来说，本讨论的目标是展示一个OpenGL应用程序，它动画一个球体，使其遵循图1中描绘的轨迹。像图2中的点一样，这个球体具有向上的初始速度但向下的加速度。

要更新球体顶点的位置，必须处理三条信息：经过的时间、速度和加速度。在本节中，我将讨论应用程序如何获取时间，然后继续展示如何计算速度、加速度和更新后的位置。

2.1 获取经过时间

要确定如何更新顶点位置，第一步是获取经过的时间。不同的窗口系统和操作系统提供不同的计时函数，但此示例应用程序中的代码基于OpenGL实用工具包，即GLUT。示例应用程序依赖两个函数来获取计时信息

1. glutIdleFunc(void (*func)(void)) – 标识当应用程序空闲时（未接收或处理事件）要调用的函数
2. glutGet(GLUT_ELAPSED_TIME) – 返回自glutInit调用以来或第一次调用glutGet(GLUT_ELAPSED_TIME)以来经过的毫秒数

要在代码中配置计时，animate_sphere.cpp文件中的主函数调用以下代码行：

glutIdleFunc(update_vertices);
start_time = glutGet(GLUT_ELAPSED_TIME);

第一行表示当应用程序空闲时应调用update_vertices函数。第二行计算start_time，它设置了以毫秒为单位的起始时间。

update_vertices函数获取当前时间并用它来计算经过的时间。以下代码展示了其工作原理

void update_vertices() {
   current_time = glutGet(GLUT_ELAPSED_TIME);
   delta_t = (current_time - start_time)/1000.0f;
   ...
} 

delta_t变量包含将用于我们物理方程的经过时间。请注意，这不是帧之间的时间，而是自应用程序启动以来经过的总时间。

2.2 处理速度和加速度

在确定计时数据之后，应用程序会计算由图形的速度和加速度引起的位置变化。在animate_sphere.cpp中，动态参数使用以下代码进行初始化：

#define INIT_POSITION 0.5f
#define INIT_VELOCITY 0.8f
#define ACCELERATION -0.4f
...
glm::vec3 init_position = glm::vec3(0.0f, INIT_POSITION, 0.0f);
glm::vec3 init_velocity = glm::vec3(INIT_VELOCITY, INIT_VELOCITY, 0.0f);
glm::vec3 acceleration = glm::vec3(0.0f, ACCELERATION, 0.0f);

如图所示，r₀被初始化为(0.0, 0.5, 0.0)，v₀被初始化为(0.8, 0.8, 0.0)，a被设置为(0.0, -0.4, 0.0)。每个都由OpenGL数学库提供的glm::vec3数据类型表示。

update_vertices函数使用以下代码计算更新后的位置向量

delta_r = init_position + delta_t * init_velocity + 0.5f * delta_t * delta_t * acceleration;

这与我们之前推导的方程相同，应该很熟悉。结果标识了每个顶点位置应如何更新，它至少可以通过两种方式使用。首先，可以将delta_r添加到包含顶点位置的VBO元素中。其次，可以将delta_r作为统一变量发送到顶点着色器，顶点着色器将把delta_r添加到每个顶点的最终位置。在OpenGL中，统一变量是不会从一个顶点到另一个顶点变化的量。

animate_sphere应用程序采用了第二种方法，以下代码将统一变量的数据设置为等于delta_r

glUniform3fv(delta_location, 1, &(delta_r[0]));

当顶点着色器执行时，它会将更新后的位置添加到图形中的每个顶点。你可以通过检查顶点着色器（animate_sphere.vert）来看到这一点，其中包含以下代码行

gl_Position = mvp * vec4(in_coords + delta, 1.0);

这表明顶点的位置被设置为原始VBO位置（in_coords）加上更新后的位置（delta）通过模型视图投影矩阵（mvp）变换后的结果。当着色器执行时，它会更新顶点位置，结果如前面图1所示。

3. 结论

如果你希望图形模型中的对象逼真移动，你需要对动力学有基本的了解。本文讨论了刚体线性动力学理论，并重点关注了位置、速度和加速度之间的关系。本文的第二部分讨论了如何将该理论在代码中实现。特别是，animate_sphere应用程序设置了球体的初始速度和加速度，用C语言计算了动态方程，并使用OpenGL渲染了它在空间中的运动。