复杂但清晰的 C# 路径查找
用于大型动态场景的半解析式二维寻路。
引言 
本文介绍了一种半解析式的寻路算法,它不需要大量的内存,在这方面与其他解决相同问题的算法有很大区别。其中大多数是图搜索算法。它绝不是万能的算法。它有其优点,也有一些缺点。我只是觉得它值得一提。你永远不知道它可能会如何帮助到某人,或者它可能会启发某人采纳它,甚至增强它以克服其局限性,并成为更有用的东西。我认为它有很大的优化潜力。
在版本 2.0 中,您还可以指定对象的宽度,而不仅仅是单个点。有新的算法(但基本上是不可用的),新的场景(除了盒子,还有圆形和线条……真是抢钱),更好的图形,以及一些优化和更正。
版本 3.0 的主要特点是场景虚拟化,这消除了对缓冲底层地图的需求。同样,包含了一些新算法。这次,它们甚至与 A* 和Evasion 算法不相上下。
背景
我对互联网上流传的各种 Dijkstra 变体感到不满意。我知道它们可以得到很好的优化,但它们似乎总是太沉重,太暴力。或者,也许是看到所有那些节点毫无意义地向外生长,而人类可以轻易地识别出它们是无用的。然后我记得大约 15 年前,我和我的朋友想出了这个算法。好吧,实际上我认为是他想出来的,所以我这样给他记功。但这更像是一个想法。它就像一块未经雕琢的钻石,等待着被打磨成有用的形状。所以我开始剔除不必要的杂物。最初,它只是在碰撞时绕着障碍物行走,左右两侧都绕。如果它在另一侧找到了点,它会选择一条更短的路径(左边或右边),然后继续前进。这种方法当然在空心(例如封闭的房间)区域存在问题。此外,它还有许多其他有问题的边缘情况。所有这些都得到了解决,并被打磨成一个功能齐全的通用算法。
Using the Code
这个部分总是让我困惑。程序员不使用代码。我们(希望)生活在和谐共处之中。我不知道该在这里放什么。我已经尽力详细注释我的代码,并希望它能自解释和易于阅读,但如果有什么不清楚的地方,你随时可以在论坛上问我。所以,随心所欲地“使用”代码吧。
那么,寻路是关于什么的?
直截了当地说,它是关于尽可能地从 A 点到达 B 点。当然,故事里也有坏人。我们称他们为障碍物。其中最糟糕的是空心障碍物,你根本进不去。你会很快开始讨厌它们。但救赎近在眼前。这个新引入的算法很喜欢它们。它像热刀切黄油一样穿过它们。不仅如此。空心物体实际上(在某种意义上)加速了这个恶魔。那么,寻路是什么?在存在的情况下,找到一条逼近最优路径的合理路径,同时避开路径上的所有障碍物。静态的或移动的。所有这些都必须尽快完成。
一种方法 API 
似乎每篇文章中的 API 都越来越简单。这次我们只有一个方法可以处理。多么美妙的简洁。这个接口在方法上有所欠缺,但在参数上弥补了。你提供起始点 (startPoint) 和目标点 (endPoint),它会尝试找到自己的路,返回最终的路径,或者不返回。如果没有找到的话。它使用映射函数来检索给定坐标处的单元(通常是二维地图中的某种节点或单元格),并使用单元函数来确定输入单元是否是障碍物。这绕过了通常需要节点实现自定义接口,以及地图具有特定格式(通常是二维数组)的常规方式。现在你可以拥有任何你想要的东西。唯一的限制是点,但这取决于实现。支点仅用于此演示的目的,因此可以在生产环境中删除,优化标志也是如此。所以,看吧,认识一下 IPathfinder。
在版本 2.0 中,我已经设法弃用了两个参数,它们现在已合并在一起,经过轻微的Evasion 算法优化。我并不特别喜欢 CodeProject 上稳定的(更不用说向后兼容的)API;似乎是这样。
public interface IPathfinder
{
Boolean TryFindPath<TMapUnit>(Point startPoint, Point endPoint,
StopFunction stopFunction, // introduced in version 2.0
MapFunction<TMapUnit> mapFunction, // deprecated in version 2.0
UnitFunction<TMapUnit>unitFunction, // deprecated in version 2.0
out IReadOnlyCollection<Point> path,
out IReadOnlyCollection<Point> pivotPoints,
Boolean optimize = true);
}
自版本 3.0 以来,我决定包含一个新的接口:IPathScenario。它已逐渐成为一个重要的组成部分。其基本实现有助于提供一些基本功能,如缓存。距离图也被移到了这里。接口本身只包含一个方法,该方法确定给定坐标处的离散单元是否被具有特定直径的物体阻塞。仅此而已。
public interface IPathScenario
{
Boolean IsBlocked(Int32 x, Int32 y, Int32 diameter);
}
简单问题的复杂实现
古老而美好的直线
此算法的核心是Bresenham's line algorithm。我使用了一个略微修改的版本来禁用对角线移动。那些会导致我称之为“无法到达的洞穴”的问题。它们可能穿过一个封闭区域,然后通过对角线出去。但此算法无法到达那里,因此会在那个洞穴中无限循环。
一个简单的想法
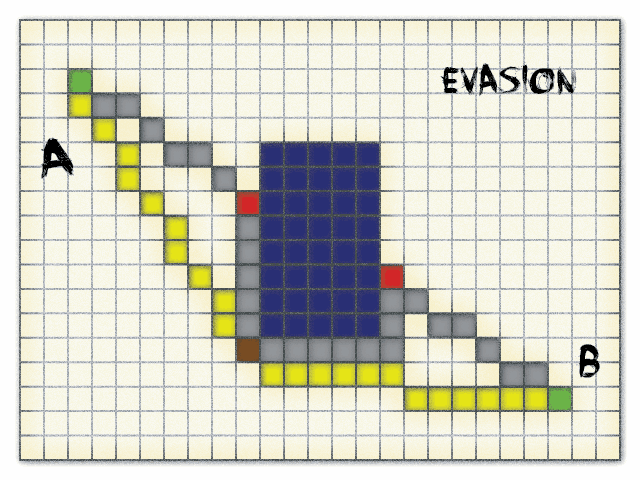
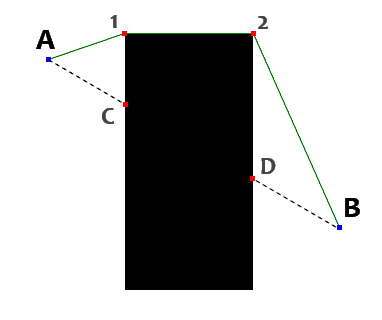
要理解这个算法真的很容易。但是,正如文章标题和本章标题所暗示的;实现不像它看起来那么容易。图 1 展示了一个简单的场景,说明了这个算法的精髓。你从 A 点(出发点)开始,然后使用上面提到的直线算法,枚举到 B 点的所有点(点将用作任何二维离散网格单元的占位符)。在处理过程中,你只跟踪外部段。在此图中,黑色表示“内部”。如你所见,你将从 A 点到达 C 点。然后检测到 C 点的碰撞,你忽略从 C 点(+一步)到 D 点(-一步)的点。然后你再次从 D 点记录到 B 点。所以在这个例子中,我们得到了两个段(A->C,D->B)。第一部分完成了。
现在我们开始一个循环,取一段,并解决它遇到的障碍物碰撞。我们将该段的路径(A->C)添加到结果中。所以现在它等于 {A, C}。然后另一个方法试图通过绕行(在本例中是左侧,但实际上应该无关紧要)来解决碰撞。我们创建了所有段的起始点列表(高于正在处理的段)。这次只有一个段 D->B。我们将 D 点存储在终点集合中。在这种情况下(图 1),检测到碰撞方向,它是东南方向。这个方向向左旋转,直到碰撞点 (C) 周围的邻居不再被阻塞。东方向仍然被阻塞,所以我们会停在北方向。然后,我们在每一步尝试从当前方向的反方向(即南)向左旋转(当然不包括反方向),确保我们沿着障碍物的形状前进。但在到达点 1(我们的第一个转角)之前,我们仍然将北方视为主要方向。在转角点(1)处,我们突然检测到东方向。我们将此转角点添加到转角点列表中(现在是 {1}),然后我们继续向东,直到再次检测到另一个转角点(2),它也添加到我们的集合中(现在是 {1, 2})。继续前进,直到遇到我们之前准备好的终点 (D)。我们注意到转角点列表的计数(此时包含 {1, 2})。这将用于分割左侧路径和右侧路径。我们还记录了此时的总步数。同样用于确定左侧路径是否比右侧路径短。然后我们继续如上所述向南,抓住点 3,然后向西,遇到点 4,最后向北,我们再次回到起始点 C。现在我们已经扫描了障碍物,并获得了一些有用的信息。我们有转角点列表 {1, 2, 3, 4},总步数(障碍物的周长),转角点列表的索引,直到该索引为止的转角点列表是左侧路径(从该索引开始,我们可以假设右侧路径),同样,我们有左侧步数(右侧步数可以通过简单计算得出:右侧步数 = 总步数 - 左侧步数),最后,遇到的终点所属的段索引。我们确定较短的路径,使用索引分割转角点列表,并将该一半添加到我们的结果列表中。如果我们没有在障碍物扫描中遇到任何终点,则终点是不可达的,我们可以立即结束寻路。处理完所有段后,我们就得到了点的结果列表。
正如我所说,哇,对于一张图几秒钟就能描述清楚的事情来说,确实很复杂。上次它对我很有用,所以我在这里附上元代码,来了:
- 找到从 A 到 B 的直线上的所有可访问段。
- 对于实际的段
- 将起始点和终点都添加到结果列表中
- 创建终点集合(正在处理的段之后的段的起始点)
- 检测碰撞方向
- 将此方向向左旋转,直到邻居未被阻塞
- 重复直到位置回到碰撞点
- 沿实际方向继续
- 从当前方向的反方向向左旋转,直到未被阻塞
- 如果方向改变,将点添加到转角点列表中
- 如果检测到终点,则记录实际的转角点计数和步数(左侧步数)
- 增加总步数
- 如果我们找到了一些终点,则将实际段设置为终点的段(下一个要处理的)
- 如果未找到,则完成,路径不存在。
- 如果左侧步数大于总步数的一半,则使用右侧路径,否则左侧路径较短
- 如果左侧路径是路径,则在转角点计数处分割转角点列表并取左半部分,否则取右半部分
- 将这些转角点添加到结果列表中(如果右侧路径较短则反转它们)。
空心威胁
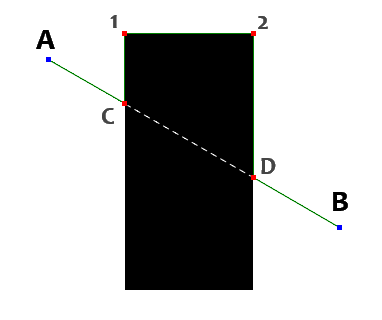
正如你在图 2 的简单场景中所见,空心区域确实很糟糕。大多数 Dijkstra 系列算法在处理这些情况时都有问题,因为它迫使它们处理图中的所有节点(将性能和内存发挥到极致)。这通常迫使它们绕过它,要么确保没有空心区域(内部有未阻塞的点),要么以某种方式预处理路径。此算法通过制作一个集合,其中包含正在处理的段之后的所有终点来跳过它们。因此,在处理第一个段 A->C(例如)时,我们会收集其他后续段(D->E,F->B)的所有起始点(现在是终点)。这给了我们 {D, F} 的集合。当我们在障碍物周围行走时遇到其中任何一个,我们就可以用它们来继续处理下一个段。正如你所见,仅仅绕着障碍物走,下一个终点 (D) 就不够了,因为我们在绕行时永远不会到达它。通过包含所有这些,我们可以跳到段 F->B,并继续处理。所以,在某种意义上,我们不仅解决了问题,还节省了绕行内部墙壁所需的时间。因此,我们利用了寻路的天敌来为我们所用。这种优势使算法对空心区域免疫,我们再也不必为此烦恼了。
改进僵尸般的行走
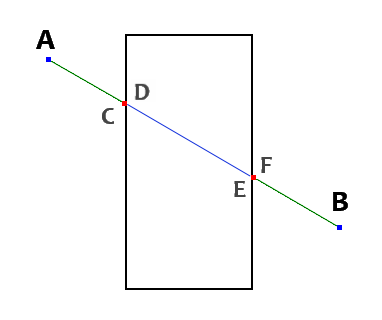
就像僵尸一样,这些愚蠢的路径需要一些头脑。此时,我们所拥有的只是真正的僵尸般的行为。直接走向目标,遇到障碍物就绕过去。我们需要某种方式来优化我们的路径,使其更合理。一种方法是使用视线来验证我们是否可以删除中间的一些点。我们首先将起始点设置为 A 点(图 3)。我们将此点添加到我们优化的结果路径中,然后从最后一个点(B,D,然后 2,然后 1)缓慢地向后移向起始点。我们再次使用 Brensenham 的直线算法来确定路径是否阻塞。当从起始点 (A) 到处理点(在这种情况下是 1)的路径未被阻塞时,我们就找到了下一步。正如你所见,我们已经优化掉了 C 点。然后我们将此点添加到结果路径中,并再次从最后一个点开始。但此时的起始点设置为最后一个可见点(1)。所以我们再次测试 1->B,1->D,1->2,找到,点 2 是我们的下一个结果点。再次 2->B,又完成(优化掉了 D 点)。这使得我们的结果列表为 {A, 1, 2}。如果我们最终到达最后一个点,我们就无法进一步处理,所以我们只需将最后一个点添加到我们的结果中,然后就完成了。这导致了一个优化的点集 {A, 1, 2, B}。即使在这个有限的场景中,我们也优化掉了两个点,路径看起来也更合理了。现在对于一个相当大的地图,我们只有四个点。这使得该算法在面对大型区域时表现出色(或内存消耗过大)。
肥胖物体移动
现在我们的物体正在智能地沿着优化路径移动,我们想要更多。我们希望我们的物体有一个额外的约束——肥胖……肥胖,好吧,为了简洁起见,我们称之为直径。与其尝试用复杂的方式修改我们的算法,不如使用预先计算的距离图。此图每场景计算一次,针对场景中的固定对象(如建筑物、河流等)。在每个像素处,它指示到最近障碍物的距离(参见图 4a-4d)。这样,我们就简单地将像素视为障碍物,如果宽度不合适的话。我们知道物体的半径,我们知道到最近障碍物的距离,所以这是一个简单的比较。这样,最终路径就已经考虑了半径。我们不必修改算法,甚至不必修改路径优化。你现在可能会问:“如果我需要一个不是圆形的形状呢?”嗯,想象一下矩形的情况。它需要转弯,而矩形一直转弯仍然是圆。所以总有一个直径。你只需要将你的形状适合进去。
 |
 |
 |
 |
|
图 4a:首先找到障碍物。
|
图 4b:将距离设置为 1 到邻居。
|
图 4c:继续将距离设置为下一波。
|
图 4d:完成完整的距离图。
|
GetPixel 必须死! 
没错。众所周知,GetPixel 速度非常慢。这促使我进行了完全的场景虚拟化。有时,地图可以通过一系列矩形(例如建筑物)或其他简单形状来更好地表示。要求先将所有内容绘制在图像上,然后使用慢速方法查找路径是残酷的。但我意识到,在某个极限(通常是几何实例的数量)之后,即使是几何解析场景也无法足够快。对于这些情况,我包含了一个巧妙的基础场景实现,它还支持通过 BitArray 进行缓存。这样,我们每 8 个像素只使用 1 字节(例如,对于 512x512 单位的地图,它只需要 32KB 存储,而不是 256KB,甚至更糟)。随机标记场景就是这样实现的,供你理解。处理五千个矩形的碰撞检测过于耗时,所以改用缓存。这时只需要一个简单的位检查。
通过虚拟化,我们终于看到了算法真实的底层性能。与之前的“GetPixel”版本相比,速度也有显著提升。
算法购物篮 
我从上次做了修改,并将在本节介绍其他可用的寻路算法。为了让读者了解本文介绍的算法的背景,我可能会在版本更新时实现其中一些算法,就像我在C# 中一个简单但功能强大的调色板量化器一文中那样。
Evasion Pathfinder(包含在版本 1.0 中)
我将其包含进来只是为了与其他算法进行比较,我试图做到客观。
|
|
|
Dijkstra 系列算法的共同点
|
|
|
A*(包含在版本 1.0 中)
这是目前最流行的寻路算法之一。它基于 Edsger Dijkstra 的图最短路径算法。它基本上是一个定向的洪水填充算法,它通过启发式方法计算到终点的距离。它在扩展时也会累积得分。当源点扩展到其邻居时,它会围绕已处理区域创建一个边界。在每一步,都会选择一个得分最好的节点,并以最高优先级(估计得分最低)进行处理。因此,你从起始点周围的邻居开始,将它们放入一个未处理坐标集中。然后选择最好的一个进行下一个处理,它的邻居再次添加到未处理邻居集中,然后从所有这些中选择下一个候选者,依此类推。因此,它正在缓慢地将边界推向目标。每个节点还记得它是由哪个节点创建的。因此,当您到达终点时,您可以回溯到起始点。这就是我们的最终路径(尽管是反向的)。如果您耗尽所有未处理的节点而未找到终点,则认为该点不可达。Dijkstra(以及类似 A*)有很多变体,它们主要在洪水定向方式以及用于计算得分的启发式方法上有所不同。
|
|
|
最佳优先搜索(包含在版本 3.0 中)
此算法又是 Dijkstra 系列的成员。它基本上是 A* 算法,只有一个启发式得分。再次执行洪水填充,检测邻居,然后评级,并立即处理具有最佳启发式得分(在这种情况下是到目标点的伪欧几里得距离)的邻居。性能与 A* 类似。有时它表现更好,通常稍差。A* 更像是进化的一步。
|
|
|
广度优先搜索和深度优先搜索(包含在版本 2.0 中)
这些又是 Dijkstra 算法的变体。它们执行洪水填充,但不是复杂的启发式方法(如 A* 的情况),而是只有 BFS 的队列(DFS 的堆)。您在找到新节点时将它们放入。已访问节点将被跳过。BFS 算法实际上让我非常惊讶,因为我没想到它会做得这么好。它对于这些类型的场景来说仍然几乎不可用,但它确实有效。它运行缓慢,但效果不错。而DFS 正是我所期望的,甚至更多。慢得令人痛苦(或者也许我做错了什么,这总是有可能的),它只是证明了它在这个场景中毫无优势。这两种算法还有其他用途,例如简单的迷宫,或者主要用于寻路领域之外的用途。
我不推荐这些。太慢,内存占用太多。
|
|
|
Dijkstra(包含在版本 2.0 中)
我最初只是想做一个荣誉提及,但它做得相当不错,所以我把它列入了。它基本上是没有启发式的 A*,或者我应该说,A* 是带有启发式的 Dijkstra。A* 的速度提升非常明显,如果不是合乎逻辑的话。它仍然做得出奇地好。我认为在大多数情况下,它胜过了 BFS 和 DFS。
我不推荐这种算法用于此处使用的大型区域。
|
|
|
Jump-point search(包含在版本 3.0 中)
我读到它应该持续优于 A*,但我无法证实这一点。我很有可能在这里犯了一些错误,但我已经从不同来源检查了很多次,它似乎是没问题的。它在某些类型的场景中表现更好,但大多数情况下表现比 A* 差很多。如果有人能发现任何问题,请告诉我。我认为效率低下源于它仍然检查跳跃方向上的点。因此,它跳过了打开节点进行处理,但在这些情况下仍然执行了StopFunction 检查。删除递归似乎没有带来太多改进。但它确实有效,在迷宫中它似乎比 A* 表现更好。
为了确定,请查看原始来源:Jump-point search。在我进行更多测试之前,我不会包含优缺点。
截图库 
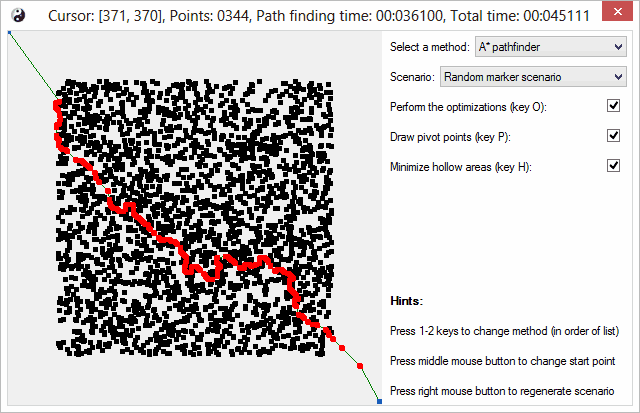
不幸的是,截图不像调色板量化那样色彩丰富而漂亮。所以我会简要展示这两张丑陋的截图。我已经尽力在艺术上进行美化,但总有极限。这张截图显示了随机标记场景(5000 个小矩形)。它用于模拟密集环境。
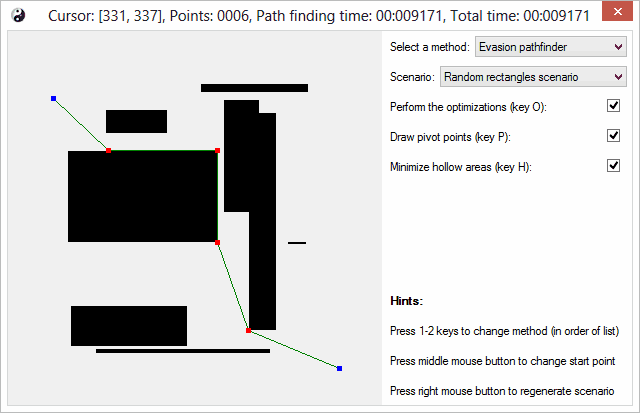
另一张屏幕显示了实际的Evasion 算法的运行情况。这个场景则模拟了包含较少大型对象的广阔空旷区域。
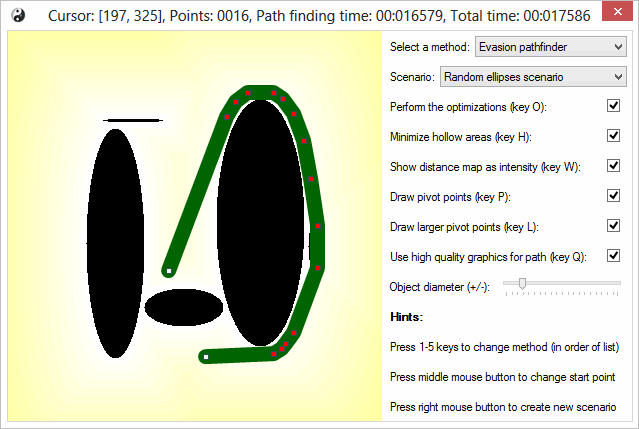
我设法加入了一些效果,以增加视觉吸引力。这张图显示了用于计算带半径对象的路径的新距离图,并演示了它在新添加的随机椭圆场景中。你还可以注意到,还有一些设置可以调整。
正如你在版本 3.0 中所见,距离图包含了边缘。在这个截图中,还显示了随机直线场景的虚拟化。一些场景现在支持碰撞检测的质量。你可以在速度和质量之间进行选择。

反馈
像往常一样,随时在下面的论坛中提问。如果你发现任何有趣的优化或功能(又名 bug ;-)),请告诉我。
相关文章
更改日志
版本 3.0
- 场景现在可以完全虚拟化
- 引入了新接口 IPathScenario
- 由于虚拟化,算法整体速度提升
- 距离图生成速度提升,地图现在是场景的一部分
- 边缘现在包含在距离图中
- 包含两个新算法
版本 2.0
- 包含新的算法和场景
- 支持物体半径(不会穿过狭窄路径)
- 现在支持高质量图形(基本上是抗锯齿)
- 更优、更快的路径优化(是的,我应该更仔细地阅读我自己的文章)
- 包含许多 bug 修复和代码更正
- 代码注释覆盖率增加
- 寻路接口已得到简化(代码词即 -> 已更改)
版本 1.0
- 发布了最初的自发版本
历史
- 2013-08-30:发布版本 3.0
- 2013-08-30:添加了部分GetPixel 必须死!
- 2013-08-24:发布版本 2.0
- 2013-08-24:添加了部分肥胖物体移动
- 2013-08-18:发布了初始文章
