65.9K
CodeProject 正在变化。 阅读更多。
Home

3D 饼图

Julijan Sribar
starIconstarIconstarIconstarIcon
emptyStarIcon
starIcon

4.94/5 (384投票s)

2004年6月7日

Zlib

9分钟阅读

viewsIcon

1277782

downloadIcon

32251

用于绘制 3D 饼图的类库

引言

最初的想法是创建一个用于绘制 3D 饼图的实用工具类/类库。起初，这似乎很简单，因为 Graphics 类中已经有一个 DrawPie 方法。该方法接受起始角度和扫描角度作为参数，因此应该不是问题：只需将所有值相加，然后计算每个值的比例，将其转换为相应饼图扇形的扫描角度。这对于圆形图来说是可行的。但是，如果您想添加 3D 透视（即，如果图表以椭圆形绘制），则此方法会导致值变化的印象，如下面的图所示：左侧和右侧的饼图扇形看起来比上下方的扇形更大，尽管它们具有相同的扫描角度。

必须使用椭圆的参数方程，而不是直接插入扫描角度。

这样就解决了上述问题，为图表添加真实的 3D 外观只需要一个额外的步骤：绘制圆柱体的边缘。但是，如果您想绘制与公共中心分开的饼图扇形，那么切面的侧面会变得可见，也必须绘制。由于这些侧面可能会部分重叠，因此绘制顺序对于获得正确的 3D 外观至关重要。

背景

绘图

首先，请注意下面的图所示的坐标系

椭圆的参数方程形式为

x = a * cos(t)

y = b * sin(t)

其中 a 和 b 分别是长半轴和短半轴，t 是变量参数。请注意，t 在角度方面没有直接的解释，但是（任何熟悉三角学的人都会从下面的图推断出）它可以与从椭圆中心开始的极角相关联，表示为

angle = tan-1(y/x) = tan-1((b * sin(t)) / (a * cos(t)))

因此，在初始化单个形状进行渲染时，必须通过以下方法转换相应的起始角度和扫描角度：

protected float TransformAngle(float angle) {
  double x = m_boundingRectangle.Width * Math.Cos(angle * Math.PI / 180);
  double y = m_boundingRectangle.Height * Math.Sin(angle * Math.PI / 180);
  float result = (float)(Math.Atan2(y, x) * 180 / Math.PI);
  if (result < 0) 
    return result + 360;
  return result;
}

在上述方法中，m_boundingRectangle 是从中切割饼图形状的椭圆的边界矩形。该矩形的宽度和高度分别等于椭圆的长轴和短轴。

绘制 3D 饼图扇形（具有一定的有限高度）时，需要绘制扇形切面以及扇形所在的圆柱体的外围。为此，必须首先计算中心点和饼图扇形外围的点（PieSlice 类中的私有成员 m_center、m_pointStart 和 m_pointEnd）以及它们在扇形底部的相应点。这些点用于构成 GraphicsPath：切面路径由四条线组成，而圆柱体外围路径由两条垂直线和两个圆弧组成。

值得注意的是，与起始角度对应的切面仅在起始角度大于 90 度且小于 270 度时可见，而与结束角度对应的切面仅在角度介于 270 度和 90 度之间时可见。同样，圆柱体边缘仅在角度介于 0 度和 180 度之间时可见。

如前所述，当图表包含多个分开的扇形时，绘制顺序很重要。必须首先绘制跨越 270 度边界的饼图形状，因为它可能被另一个饼图扇形（部分）覆盖。然后绘制最接近 270 度轴的扇形（无论它是来自左侧还是右侧），然后对后续的扇形重复此过程。

为了实现此顺序，饼图扇形存储在一个数组中，从跨越 270 度轴的形状开始。因此，相邻的形状将放置在数组的第二个和最后一个位置。因此，搜索要绘制的下一个形状会同时从列表的开头和结尾进行，选择更接近 270 度轴的形状以首先绘制。

跨越 270 度轴的饼图扇形具有一个独特的特征：两个切面（对应于起始角度和结束角度）都可见 - 参见下图左侧。此外，如果起始角度和结束角度都在 0 度到 180 度范围内，则该扇形的圆柱体边缘将由两部分组成（下图右侧）。为了处理这种情况，在绘制过程中，该扇形被分成两个子扇形，具有共同的顶部。

这种分割在绘制下图所示的图表时发挥作用：如果首先完全绘制蓝色扇形，绿色扇形将完全覆盖它，导致不规则的视觉效果。每个形状上的数字表示正确的绘制顺序。

命中检测

当文章的第一个版本发布时，一些读者建议添加鼠标悬停时的工具提示和饼图扇形高亮显示。此功能已在 1.1 版本中实现。

主要问题是找到并实现搜索当前鼠标光标所在的饼图扇形的算法。整个图表的搜索顺序与绘制顺序相反，从最前面的扇形开始。但是，由于单个扇形形状不规则，因此处理起来很麻烦。

为了测试饼图是否被命中，必须将饼图扇形分解成几个表面，如下图所示，并测试这些表面中的每一个是否包含命中点。

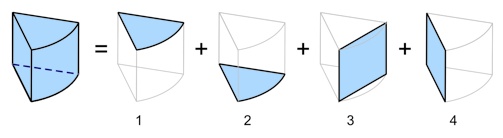
请注意，圆柱体外围的命中测试不是直接进行的（实际上，我不知道如何简单地做到），而是通过测试顶部（1）和底部（2）的饼图表面以及由外围点定义的四边形（3）来覆盖的。

顶部和底部扇形表面的命中测试很简单 - 将点到椭圆中心的距离与相应角度的椭圆半径进行比较。

private bool PieSliceContainsPoint(PointF point, 
            float xBoundingRectangle, float yBoundingRectangle, 
            float widthBoundingRectangle, float heightBoundingRectangle, 
            float startAngle, float sweepAngle) {
  double a = widthBoundingRectangle / 2;
  double b = heightBoundingRectangle / 2;
  double x = point.X - xBoundingRectangle - a;
  double y = point.Y - yBoundingRectangle - b;
  double angle = Math.Atan2(y, x);
  if (angle < 0)
    angle += 2 * Math.PI;
  double angleDegrees = angle * 180 / Math.PI;
  // point is inside the pie slice only if between start and end angle
  if (angleDegrees >= startAngle && 
             angleDegrees <= startAngle + sweepAngle) {
    // distance of the point from the ellipse centre
    double r = Math.Sqrt(y * y + x * x);
    double a2 = a * a;
    double b2 = b * b;
    double cosFi = Math.Cos(angle);
    double sinFi = Math.Sin(angle);
    // distance of the ellipse perimeter point
    double ellipseRadius = 
           (b * a) / Math.Sqrt(b2 * cosFi * cosFi + a2 * sinFi * sinFi);
    return ellipseRadius > r;
  }
  return false;
}

对于四边形，使用一个众所周知的算法来测试点是否在多边形内：从要测试的点发射一条射线，并计算该射线与多边形的交点数。如果交点数为奇数，则点在多边形内部；如果为偶数，则点在多边形外部（参见下图）。

因此，所有多边形部分都会被遍历，计算与射线的交点。

public bool Contains(PointF point, PointF[] cornerPoints) {
  int intersections = 0;
  float x0 = point.X;
  float y0 = point.Y;
  for (int i = 1; i < cornerPoints.Length; ++i) {
    if (DoesIntersect(point, cornerPoints[i], cornerPoints[i - 1]))
      ++intersections;
  }
  if (DoesIntersect(point, cornerPoints[cornerPoints.Length - 1], 
                                                cornerPoints[0]))
    ++intersections;
  return (intersections % 2 != 0);
}

private bool DoesIntersect(PointF point, PointF point1, PointF point2) {
  float x2 = point2.X;
  float y2 = point2.Y;
  float x1 = point1.X;
  float y1 = point1.Y;
  if ((x2 < point.X && x1 >= point.X) || 
      (x2 >= point.X && x1 < point.X)) {

      float y = (y2 - y1) / (x2 - x1) * (point.X - x1) + y1;
      return y > point.Y;
  }
  return false;
}

Using the Code

PieChart 解决方案包含三个类：PieSlice、PieChart3D 和 PieChartControl（继承自 System.Windows.Forms.Panel 控件）。PieSlice 类提供了使用给定的起始角度、扫描角度、颜色、高度和阴影样式绘制 3D 饼图扇形所需的所有功能。

PieChart3D 表示整个图表。有几种可用的构造函数，它们都接受一个边界矩形和一个值数组。一些构造函数还接受

  • 用于表示值的颜色数组
  • 扇形位移数组
  • 扇形厚度

扇形位移表示为扇形“深度”与椭圆半径之比；最小值为 0 表示没有位移，而 1（允许的最大值）表示形状完全从椭圆中移出。

扇形厚度表示饼图扇形厚度与椭圆垂直短轴之比；允许的最大值为 0.5。

还可以通过公共属性设置以上任何参数。请注意，如果提供的颜色数量少于值的数量，颜色将重复使用。同样，如果位移数量用尽，最后一个位移将用于所有剩余的饼图扇形。

还有一些附加的 public 属性可以设置

  • 文本,
  • 字体
  • ForeColor
  • 阴影样式
  • 边缘颜色类型
  • 边缘线宽
  • 初始角度
  • 适合边界矩形

所有这些属性的含义及其可能的值可以在演示示例中看到。Texts 属性是一个字符串数组，显示在相应的扇形上。默认实现将文本放置在扇形顶部中心附近，但用户可以覆盖 PieChart3D 类的 PlaceTexts 方法来实现自己的放置逻辑。Font 和 ForeColor 属性定义用于显示这些文本的字体和颜色。

PieChart3D 类可用于打印：只需初始化图表对象，然后调用其 Draw 方法，提供相应的 Graphics 对象即可。

public void Draw(Graphics graphics) { ... }

要在屏幕上显示图表，PieChartControl 更合适：它将图表封装到一个面板中，该面板负责图表（重新）绘制。用户只需将其放置在窗体上并设置所需的值。例如：

private System.Drawing.PieChart.PieChartControl panelDrawing = 
  new System.Drawing.PieChart.PieChartControl();
panelDrawing.Values = new decimal[] { 10, 15, 5, 35};
int alpha = 80;
panelDrawing.Colors = new Color[] { Color.FromArgb(alpha, Color.Red), 
                                    Color.FromArgb(alpha, Color.Green), 
                                    Color.FromArgb(alpha, Color.Yellow), 
                                    Color.FromArgb(alpha, Color.Blue) };
panelDrawing.SliceRelativeDisplacements = new float[] { 0.1F, 0.2F, 0.2F, 0.2F };
panelDrawing.Texts = new string[] { "red", 
                                    "green", 
                                    "blue", 
                                    "yellow" }; 
panelDrawing.ToolTips = new string[] { "Peter", 
                                       "Paul", 
                                       "Mary", 
                                       "Brian" };
panelDrawing.Font = new Font("Arial", 10F);
panelDrawing.ForeColor = SystemColors.WindowText
panelDrawing.LeftMargin = 10F;
panelDrawing.RightMargin = 10F;
panelDrawing.TopMargin = 10F;
panelDrawing.BottomMargin = 10F;
panelDrawing.SliceRelativeHeight = 0.25F;
panelDrawing.InitialAngle = -90F;

PieChartControl 重写了 OnPaint 和 OnResize 事件，负责正确的图表重绘。

请注意，PieChartControl 还有一个附加的 ToolTips 属性，接受一个字符串数组，当命中相应的饼图扇形时显示这些字符串。如果此数组中的任何字符串为空，则将显示相应的值。

关注点

为了获得更好的 3D 透视效果，我引入了“渐变”阴影，根据切面角度改变切面的亮度。为了在圆柱体边缘上实现这种效果，使用了渐变填充来绘制外围。我为此使用了一个经验公式。但是，用户可以通过派生 PieSlice 类并重写 PieSlice 类中的 CreateBrushForSide 和 CreateBrushForPeriphery 方法来更改这一点，从而实现自己的逻辑。

同样，用户可以覆盖 PieChart 类中的 CreatePieSliceHighlighted 方法；默认实现以略浅的颜色绘制高亮显示的饼图扇形。

从 1.4 版本开始，演示程序中包含了一个简单的饼图打印功能；用户只需单击演示窗体上的“打印”按钮。打印代码在 Test 项目的 PrintChart 类中提供。

版权声明

您可以自由使用此代码和附带的 DLL。请在荣誉榜中引用此网页。

历史

  • 2004 年 6 月 1 日 - 文章首次提交
  • 2004 年 6 月 22 日 - ver. 1.1：添加了工具提示和饼图扇形高亮显示。此外（这些功劳归功于 Andreas Krohn），已移除调整大小时的闪烁，并修复了控件非常小时的断言失败错误。
  • 2004 年 11 月 11 日 - ver. 1.2：错误修复
  • 2005 年 3 月 21 日 - ver. 1.3：添加了颜色透明度支持（感谢 Bogdan Pietroiu 的建议），并添加了每个扇形的描述文本（如 ccarlinx 所建议）。
  • 2005 年 11 月 10 日 - ver. 1.4：修复了饼图控件在角度为 270 度时崩溃的错误（由 gabbyr 和 rafabgood 发现）以及“当所有扇形值为 0 时崩溃”。在演示项目中包含了一个简单的饼图打印示例（请注意，打印质量取决于打印机的性能，通常远不如屏幕显示质量）。
  • 2006 年 3 月 12 日 - ver. 1.5：修复了控件崩溃的错误（如 jianingy 所指出的）。
© . All rights reserved.