随机想法……

John Underhill

4.93/5 (45投票s)

2014 年 6 月 29 日

CPOL

41分钟阅读

74977

1286

C# 中的 CSRG 随机生成器和 NIST STS 库（重大更新！）

下载 Drbg_Test.zip - 469 KB

有时……

你不得不把一切都丢弃，然后重新开始，（叹气）。我就是这么做的，如果你以前来过这篇文章，你会注意到我之前测试过的所有创建随机数据的方法都消失了……但相信我，这是一件好事。所以，我昨晚绞尽脑汁，试图想出如何让它更强大，也就是说，fortify 它以抵抗任何逆向尝试，同时，也许通过算法产生更好的随机数。下面是我迄今为止最好的想法的结合，我相信它能够创建一个非常出色的随机数生成器，并极度关注安全性。所以请继续阅读，很多内容已经改变，我认为这可能是其中的关键……我保留了所有原始算法，并添加了我在实验中创建的新算法（稍后会详细介绍），总之，我认为这确实值得重读……哦，我还给它重新命名为：Chaotic State Random Generator，CSRG（昵称：Chaos）。我认为这是个更好的名字……

7 月 24 日：又有一些重大更新！

今天我将它集成到我的主项目中，并对这个生成器进行了一些重大更改，所以我想让你知道……我在 Generate() 方法的主循环中添加了一个熵收集器。它收集字节，并定期提取熵，然后用它来旋转扩展表（在 Generate() 方法细分的“表旋转”部分进行了解释）。我将两个引擎的种子大小增加到 96，现在在 DUAL 引擎中，AES 密钥和计数器完全用种子材料初始化；在 SINGLE 模式下，其余 32 字节被丢弃到熵池中。我还将推荐的块大小从 10 KiB 更改为 100 KiB，这将使其在测试实现中伪随机输出与所需种子材料的比例达到大约 1000:1。

7 月 25 日：并行示例

在 frmNist 中添加了一个测试方法，演示了如何在 Parallel For 循环中使用 CSRG，ParallelTest(Size)。使用这种技术，我的 AMD A6-3600 四核处理器的吞吐量几乎达到每分钟 900 MiB。

它总是始于……

……你需要的东西。我需要一个非常好的随机数生成器；一个可以手动播种，自包含，并且性能卓越的。于是我的搜索开始了……穿过那些对速记上瘾的内向者写的无法理解的 C 代码的狂野苔原，那些额头像滑板一样大的家伙们写的数学巫术，Blum Blum Schub、Yarrow 和 Fortuna、Twister 和 ISSAC，然后……我开始研究在计数器模式下运行的块密码。我当时已经有一个 Aes 类，主要基于mono 实现，所以这应该很简单！我的第一个计数器模式实现给了我很好的结果，但使用 Ent 作为指南进行测试，它就是无法击败 Windows 内置的 api RNGCryptoServiceProvider，这是 CryptGenRandom api 的托管包装器。所以我开始实验，并用 Ent 测试的 C# 版本，后来又用 Nist 随机测试批处理，扩展了我的随机测试工具包。

标准

以下是我对该实现的期望

它必须每次都以相同的种子生成相同的随机输出
它必须快速
它必须极难被破解
它必须产生优秀的随机输出

好东西

让我们从小处着手，例如生成 16 字节的随机整数，并为生成器创建种子。第一个方法用于创建随机整数，它取自 CSPRNG 类，它获取一个随机缓冲区（在本例中来自 RNGCryptoServiceProvider），获取其 SHA256 的哈希值，并返回该哈希值的前一半。整数通过 BitConverter 重载之一从字节中绘制。这些方法都包含在静态类 CSPRNG.cs 中。

/// <summary>
/// Get a 16 byte/128 bit seed
/// </summary>
/// <returns>Random seed [byte[]]</returns>
internal static byte[] GetSeed16()
{
    byte[] data = new byte[64];
    byte[] result = new byte[16];

    _rngRandom.GetBytes(data);
    // copy first half of hash in
    Buffer.BlockCopy(_shaHash.ComputeHash(data), 0, result, 0, 16);

    return result;
}

该类包含返回所有整数和浮点类型随机数的方法，它们看起来像这样……

/// <summary>
/// Get a random 32bit integer
/// </summary>
/// <returns>Random Int32</returns>
internal static Int32 NextInt32()
{
    return BitConverter.ToInt32(GetSeed16(), 0);
}

一个随机生成器需要一个随机种子作为其初始状态，你可以发挥创意做这样的事情

/// <summary>
/// Get a 64 byte/512 bit seed
/// </summary>
/// <returns>Random seed [byte[]]</returns>
internal static byte[] GetSeed64()
{
    byte[] data = new byte[128];
    byte[] seed = new byte[64];

    _rngRandom.GetBytes(data);

    // entropy extractor
    using (SHA512 shaHash = SHA512Managed.Create())
        Buffer.BlockCopy(shaHash.ComputeHash(data), 0, seed, 0, 64);

    return seed;
}

在这个例程中，我们正在使用 RNGCrypto 生成 128 字节的随机数据，这与 SHA512 的块大小对齐，然后返回该随机数组的哈希值。这被称为“熵提取”，它涉及获取一个秘密的随机值并导出其哈希值，然后将其用作随机源，这是构建加密密钥、IV 或种子的好方法……（现在，为了给生成器播种的目的，我认为这可能有点过头了，RngCrypto 的输出应该足够好了……你甚至可能因为走得太远而丢失熵；o)

CSRG 随机生成器

在我们开始查看这个（嗯，有点吓人的算法）之前，我将从头开始，在生成器初始化时开始……

/// <summary>
/// Initialize the generator
/// </summary>
public CSRG()
{
    // use the default table seed
    _expansionTable = ExpandTable(SEED_TABLE);
}

/// <summary>
/// Initialize the generator with a unique internal expansion table
/// </summary>
/// <param name="TableSeed">Generator key: must be 48 bytes of random data</param>
public CSRG(byte[] TableSeed)
{
    // wrong seed size!
    if (TableSeed.Length != 48)
        throw new ArgumentOutOfRangeException("Expansion Seed size must be 48 bytes long!");

    _expansionTable = ExpandTable(TableSeed);
}

正如你所看到的，有两个构造函数，它们都创建了一个称为“扩展表”的东西。第一个使用默认的本地字节数组，第二个，用户输入一个 48 字节的随机数组，这，为了更好的描述，就是生成器的密钥。只翻转该数组中的一个比特，CSRG 就会产生完全不同的随机输出，即使具有相同的种子。所以，它确实有点像一个 384 位密钥，当与用作每次 Generate(Buffer) 调用中初始状态的种子结合时，为生成器增加了一层fortification。那么，它有什么真正用处呢……我做了一个加密软件，它是一个非常复杂的软件，具有调试器防篡改、安全擦除、擦除触发器、反胁迫策略、加密内存、双重加密登录、加密状态/日志/数据库、导入原始随机二进制以实现真正的 OTP，等等……所有这些都 housed 在我能想象的最酷的 wpf 界面中……所以，我过去 8 个月确实在这个东西上有点疯狂，但现在它即将结束，我正在编写帮助文件。

我一直在脑海中重温的一件事是，归根结底，它是一个 AES CTR，按照 80090 规范编写，但仍然，如果你知道那台机器真正是如何工作的，并且你看到了规范细节之外的东西，它只是一个在计数器模式下运行的块密码，并没有比这更复杂的东西。那么我们如何让它变得更好呢？我的意思是，AES 出来的任何东西都会高度随机化，尤其是 CTR，所以它在创建随机数方面做得很好，但是……

首先，关于我的那个小 xor 密码是如何工作的，一些细节

首先，我在消息头中不透露任何信息。它看起来像这样

Flag - 只是一个标识，告诉我们这是一个有效消息，始终相同
Position - 不是实际位置，而是与密钥头中的随机 ulong 偏移
Creator - 一个唯一的 16 字节字段，标识用于加密此文件的密钥
Extension - 文件扩展名，与密钥头字段中的随机数进行异或

密钥头看起来像这样

EngineType - AES 或 OTP
Position - 当前在密钥文件中的虚拟位置
KeyOffset - 一个随机的 ulong，当从消息位置减去它时，它会显示“实际”位置，如果密钥完全展开的话
KeyID - 唯一的 16 字节密钥标识
MessageHash - 16 字节的随机数，与文件扩展名进行异或
TableKey - 就是它…… 48 字节的随机数，用于解锁生成器

密钥的其余部分只是种子材料，所以一个 1MiB 的密钥文件将包含 10482 个种子，这将扩展到大约 1023 MiB 的随机数据（因此大约是 1000:1 的比例）。消息通过提取必要的种子，生成随机数，然后与数据进行异或来即时加密和解密。

那么攻击者真正拥有什么有用信息呢？如果没有密钥文件本身，他就无法知道密钥文件的大小，更不用说位置了，也不知道用于异或消息的随机数是从第一个种子的第一个字节开始，还是从第 90 个块的第 317 个字节开始……（在我实现中，种子构建到 102400 字节的“块”），一个 10 MiB 的文件将使用大约 100 个种子……所以只花费了大约 9.7 KiB 的密钥空间来加密该文件。

现在闪存驱动器的容量已达到…… 256 GB，你可以存储大约 2,748,779,069 个种子……所以你可以加密大约 260 TiB 的数据，仅凭一个闪存驱动器的密钥材料……因此，考虑到便携式存储设备容量的不断增加，OTP 或伪 OTP 已成为强大加密的一种可行手段。

我为什么要告诉你所有这些……嗯，是为了向你展示如何使用一个好的随机数生成器来构建一些非常强大的加密，并向你展示该密码是如何构建的。构建此密码最重要的任务之一是隐藏消息中可能有助于解密的任何信息，而也许最重要隐藏的细节是隐藏密钥文件中的位置偏移，特别是如果密钥是通过确定性算法生成的。好了，稍后再谈密码……

表是如何构建的？

这只是一个直接的 AES CTR 实现，它生成 4096 字节的随机数，这些随机数被复制到一个包含 1024 个成员的 Uint32 数组中……

/// <summary>
/// Transform a seed into a 1024 UInt32 array of random.
/// </summary>
/// <param name="Seed">Random seed, Fixed size: must be 64 bytes long</param>
/// <returns>Random data [byte[]]</returns>
private UInt32[] ExpandTable(byte[] Seed)
{
    const int SIZE = 4096;

    UInt32[] exTable = new UInt32[1024];
    UInt32[] exKey = new UInt32[AESEXPANDED_KEYSIZE];
    byte[] ctrBuffer = new byte[BLOCK_SIZE];
    byte[] keyBuffer = new byte[KEY_BYTES];
    byte[] outputBlock = new byte[BLOCK_SIZE];
    byte[] outputData = new byte[SIZE];

    // copy the seed to key, iv, and counter
    Buffer.BlockCopy(Seed, 0, keyBuffer, 0, KEY_BYTES);
    Buffer.BlockCopy(Seed, KEY_BYTES, ctrBuffer, 0, BLOCK_SIZE);

    // expand key
    exKey = ExpandKey(keyBuffer);

    for (int i = 0; i < SIZE; i += BLOCK_SIZE)
    {
        // increment counter
        Increment(ctrBuffer);
        // transform the counter
        Transform(ctrBuffer, outputBlock, exKey);
        // copy transform to output
        Buffer.BlockCopy(outputBlock, 0, outputData, i, BLOCK_SIZE);
    }

    // copy to table array
    Buffer.BlockCopy(outputData, 0, exTable, 0, SIZE);
    return exTable;
}

因此，计数器和 AES 密钥是从表种子中复制的，16 字节的计数器在每次迭代时增加一个比特，然后用 AES 加密，这个变换被复制到输出缓冲区，最后复制到 uint 数组。

表是如何使用的？

该表用于数组扩展和随机化例程，称为提取方法（ExtractArray16(Buffer)、ExtractArray32(Buffer)），这些例程的作用是，将数组扩展到 64 字节（以匹配 SHA256 的块大小），同时通过与扩展表进行异或来随机化它……整个装置用于一个自重新播种方案，我们稍后将对此进行探讨。ExtractArray32() 看起来像这样

/// <summary>
/// Expand an array with bit shifting
/// </summary>
/// <param name="SubBuffer">Buffer to expand</param>
/// <returns></returns>
private byte[] ExtractArray32(byte[] SubBuffer)
{
    UInt32[] tmpNum = new UInt32[8];
    UInt32[] arrNum = new UInt32[16];
    byte[] data = new byte[64];
    Int32 ct = 0;

    // copy first array in
    Buffer.BlockCopy(SubBuffer, 0, tmpNum, 0, 32);
    // get the first buffer table index
    UInt16 iter = ExtractShort(tmpNum[0], 10);

    // randomize the bits
    for (int i = 0; i < 8; i++)
    {
        arrNum[ct++] = ~tmpNum[i] ^ _expansionTable[iter];
        iter = ExtractShort(arrNum[ct - 1], 10);
        arrNum[ct++] = tmpNum[i] ^ _expansionTable[iter];
        iter = ExtractShort(arrNum[ct - 1], 10);
    }

    // copy it to byte array
    Buffer.BlockCopy(arrNum, 0, data, 0, 64);

    // get the hash
    return ComputeHash64(data);
}

所以缓冲区输入（AES 变换的 32 字节组合）……字节缓冲区被复制到一个临时的 UInt32[8] 数组，然后提取到一个更大的 16 成员的 UInt32 数组，然后将其复制回一个字节数组，并用 SHA256 进行哈希，这就是实际的返回值。第一个数组成员被一元反转并使用一个秘密索引与扩展表进行异或（索引是前一个值的最后 8 位（8 位=0-1023）），第二个值仅与另一个表值进行异或，使用从它之前的值派生的索引……依此类推。所以这就是如何生成新的 AES 密钥和新的 16 字节计数器用于主方法。我们使用 Whitening 在数据进入 SHA256 之前对其进行打乱，这确保了我们每次都能获得唯一的哈希值。现在，你可以看到，如果表种子以任何方式被更改，它将意味着一个截然不同的偏移表，进而意味着在生成器重新播种自身时创建的种子和计数器也不同。

生成器

生成器有两个方面：随机数的创建方式以及重新播种机制的工作方式。随机数是通过运行**两个 AES CTR 变换**来创建的，每个变换都有自己的**唯一密钥**和 16 字节**计数器**。在每次循环结束时，**两个变换**被**异或**在一起，结果数组被复制到输出缓冲区。就这样简单。

混乱的重新播种

除了密钥和计数器，还运行着**两个随机迭代计数器**（reSeedCounter1 和 reSeedCounter2），一个用于一个 AES 变换。在主循环的每次迭代中，它们都独立地被测试是否能整除差值。也就是说；当 (ReSeedCounterX % 256 == 0) 时，它会触发该 AES 变换的状态重置。当发生这种情况时，最后两个变换被组合并发送到 ExpandArray32() 例程，该例程会扩展和打白数据，然后返回 SHA256 哈希，该哈希被扩展为一个新的 AES 密钥。新计数器通过将一个块发送到 ExpandArray16() 例程来创建，而 UInt64 reSeedCounter 用于该变换是通过将 16 字节 CTR 计数器的两半进行异或来创建的。因此，由于两个重新播种计数器是随机的，并且由于两个变换都有唯一的重新播种计数器，调试算法就像看赛马……变换 1 将领先，连续重置状态三次，然后变换 2 将赶上并超越它，它们来回交替……重点是，这两种 AES 变换（异或在一起以创建输出）正在不断地、不可预测地更换其状态……这一切都应该结合起来，使密码分析，嗯，有点困难……这就是它的样子

/// <summary>
/// Dual-CTR Chaotic ReSeed Random Generator:
/// Generate a block of random bytes using dual AES CTR mode.
/// Uses a dual CTR xor with a chaotic state change machine.
/// </summary>
/// <param name="Size">Size of data return in bytes</param>
/// <param name="Seed">Random seed, Fixed size: must be 96 bytes long</param>
/// <returns>Random data [byte[]]</returns>
private byte[] GenerateT2(Int32 Size, byte[] Seed)
{
    // too large!
    if (Size > ENGINE_MAXPULL)
        throw new ArgumentOutOfRangeException("The size requested is too large! Maximum is "
            + ENGINE_MAXPULL.ToString() + " bytes.");
    // wrong seed size!
    if (Seed.Length != DUAL_SEED_BYTES)
        throw new ArgumentOutOfRangeException("Seed length must be " + DUAL_SEED_BYTES.ToString() + " bytes long!");

    UInt16 poolSize = 0;
    // align to upper divisible of block size
    Int32 alignedSize = (Size % BLOCK_SIZE == 0 ? Size : Size + BLOCK_SIZE - (Size % BLOCK_SIZE));
    Int32 lastBlock = alignedSize - BLOCK_SIZE;
    UInt64 reSeedCounter1 = 0;
    UInt64 reSeedCounter2 = 0;
    UInt32[] exKey1;
    UInt32[] exKey2;
    byte[] ctrBuffer1 = new byte[BLOCK_SIZE];
    byte[] ctrBuffer2 = new byte[BLOCK_SIZE];
    byte[] keyBuffer1 = new byte[KEY_BYTES];
    byte[] keyBuffer2 = new byte[KEY_BYTES];
    byte[] outputBlock1 = new byte[BLOCK_SIZE];
    byte[] outputBlock2 = new byte[BLOCK_SIZE];
    byte[] outputData = new byte[Size];
    byte[] seedBuffer = new byte[KEY_BYTES];

    const Int32 SUPPRESSOR = 32;

    // copy seed to key1, key2
    Buffer.BlockCopy(Seed, 0, keyBuffer1, 0, KEY_BYTES);
    Buffer.BlockCopy(Seed, KEY_BYTES, keyBuffer2, 0, KEY_BYTES);

    // copy seed to counter 1
    Buffer.BlockCopy(Seed, KEY_BYTES * 2, ctrBuffer1, 0, BLOCK_SIZE);
    // copy remainder to counter 2
    Buffer.BlockCopy(Seed, (KEY_BYTES * 2) + BLOCK_SIZE, ctrBuffer2, 0, BLOCK_SIZE);

    // expand AES key1
    exKey1 = ExpandKey(keyBuffer1);
    // expand AES key2
    exKey2 = ExpandKey(keyBuffer2);

    // extract the state reset counters
    reSeedCounter1 = ExtractULong(ctrBuffer1);
    reSeedCounter2 = ExtractULong(ctrBuffer2);

    for (int i = 0; i < alignedSize; i += BLOCK_SIZE)
    {
        // increment counter1
        Increment(ctrBuffer1);
        // increment counter2
        Increment(ctrBuffer2);

        // aes transforms //
        // encrypt counter1 (aes: data, output, key)
        Transform(ctrBuffer1, outputBlock1, exKey1);
        // encrypt counter2 (aes: data, output, key)
        Transform(ctrBuffer2, outputBlock2, exKey2);

        // independant random rekey mechanism for transforms 1 and 2
        if (reSeedCounter1 % _differential == 0)
        {
            // Reset State 1 //
            // copy the 2 transforms to the new seed
            Buffer.BlockCopy(outputBlock2, 0, seedBuffer, 0, BLOCK_SIZE);
            Buffer.BlockCopy(outputBlock1, 0, seedBuffer, BLOCK_SIZE, BLOCK_SIZE);
            // create new key via sha256
            keyBuffer1 = ExtractArray32(seedBuffer);
            // expand the aes key
            exKey1 = ExpandKey(keyBuffer1);
            // create a new counter
            ctrBuffer1 = ExtractArray16(outputBlock2);
            // get the int64 reseed counter
            reSeedCounter1 = ExtractULong(ctrBuffer1);
        }
        // re-state when remainder of modulo with counter is 0
        if (reSeedCounter2 % _differential == 0)
        {
            // Reset State 2 //
            // copy the 2 transforms to the new seed
            Buffer.BlockCopy(outputBlock1, 0, seedBuffer, 0, BLOCK_SIZE);
            Buffer.BlockCopy(outputBlock2, 0, seedBuffer, BLOCK_SIZE, BLOCK_SIZE);
            // create new key via sha256
            keyBuffer2 = ExtractArray32(seedBuffer);
            // expand the aes key
            exKey2 = ExpandKey(keyBuffer2);
            // create a new counter
            ctrBuffer2 = ExtractArray16(outputBlock1);
            // get the int64 reseed counter
            reSeedCounter2 = ExtractULong(ctrBuffer2);
        }

        // Entropy collector //
        // number of bytes to pass to entropy collector
        // determined by last 4 bits of output block 2
        if (reSeedCounter1 % SUPPRESSOR == 0)
        {
            // get the size
            poolSize = ExtractShort(outputBlock2, 4);
            if (poolSize > 0)
            {
                // copy to array
                byte[] pool = new byte[poolSize];
                Buffer.BlockCopy(outputBlock1, 0, pool, 0, poolSize);
                // send the bytes to the entropy pool
                EntropyPool(pool);
            }
        }
        // collect from second block
        if (reSeedCounter2 % SUPPRESSOR == 0)
        {
            poolSize = ExtractShort(outputBlock1, 4);
            if (poolSize > 0)
            {
                byte[] pool = new byte[poolSize];
                Buffer.BlockCopy(outputBlock2, 0, pool, 0, poolSize);
                // send the bytes to the entropy pool
                EntropyPool(pool);
            }
        }

        // xor the two transforms
        for (int j = 0; j < BLOCK_SIZE; j++)
            outputBlock1[j] ^= outputBlock2[j];

        // copy to output
        if (i != lastBlock)
        {
            // copy transform to output
            Buffer.BlockCopy(outputBlock1, 0, outputData, i, BLOCK_SIZE);
        }
        else
        {
            // copy last block
            int finalSize = (Size % BLOCK_SIZE) == 0 ? BLOCK_SIZE : (Size % BLOCK_SIZE);
            Buffer.BlockCopy(outputBlock1, 0, outputData, i, finalSize);
        }

        reSeedCounter1++;
        reSeedCounter2++;
    }
    return outputData;
}

表旋转

所以我们有了扩展表，正如你现在所知，它用于扩展例程，在这些例程中为内部状态转换创建新的密钥和计数器。那么，如果我们可以在运行时改变那个表，在不规则的间隔重复填充新的偏移值呢？如果你查看上面的代码，你会发现在“熵收集器”注释下的例程底部有几行。这段代码的作用是抓取几个字节并将它们传递给一个名为 EntropyPool(Buffer) 的方法。对于两个变换中的每一个都有一个子句，它使用 (reSeedCounterX % SUPPRESSOR == 0) 余数来减慢速度，它从另一个变换的最后 4 位获取要发送到熵池的字节数。它可能传递 1 到 15 字节到池中，数量取决于那 4 位是什么……所以它只是零星地窃取一些字节，大约每创建 4000 字节的输出（可通过 SUPPRESSOR 常量调整，该常量设置为 32），它就会触发扩展表的重建，给它一套全新的值。EntropyPool() 方法看起来像这样

/// <summary>
/// Collects entropy for the expansion table rotation
/// </summary>
/// <param name="Data">byte array, length 1-128</param>
private void EntropyPool(byte[] Data)
{
    int count = Data.Length;

    // to max 128 bytes
    if (count + _entropyCount > 128)
        count = 128 % _entropyCount;

    // copy it in
    Buffer.BlockCopy(Data, 0, _tableEntropy, _entropyCount, count);
    // update the counter
    _entropyCount += count;

    // triggers expansion table rotation
    if (_entropyCount == 128)
    {
        byte[] data = new byte[64];
        byte[] tableSeed = new byte[48];

        // copy the poll to 64 byte buffer
        Buffer.BlockCopy(_tableEntropy, 0, data, 0, 64);
        // get hash from sha256
        byte[] entropy = ComputeHash64(data);
        // copy to the tables seed
        Buffer.BlockCopy(entropy, 0, tableSeed, 0, 32);

        // do the same for the next 64 bytes
        Buffer.BlockCopy(_tableEntropy, 64, data, 0, 64);
        entropy = ComputeHash64(data);
        // copy to table seed
        Buffer.BlockCopy(entropy, 0, tableSeed, 32, 16);

        // create a new expansion table
        _expansionTable = ExpandTable(tableSeed);
        // reset the counter
        _entropyCount = 0;
    }
}

这里没有什么太复杂的……字节被复制到一个类变量 _tableEntropy，当字节数达到 128 时，该数组的两个一半被传递给 SHA256，它们的返回值构建了 48 字节的生成器密钥，然后用于重建或“旋转”扩展表。

那么让我们总结一下到目前为止对我们那个小 xor 密码的分析

坏家伙，拿到一个 10 MiB 的消息，他可以推断出

什么都没有。他不知道随机数是从密钥的第一个种子中提取的，还是最后一个，也不知道从该种子派生的随机数的第一个字节，还是最后一个字节。他不知道一个不可预测的内部状态机何时、何地、如何更换了密钥和计数器。他甚至不知道那是什么类型的文件！

那个 10 MiB 的文件需要 100 个种子来构建，所以攻击者必须猜测：AES(key + counter) 2 * 100 次才能读取该文件，——但是，你还必须加入内部随机状态重置。当种子计数器的模数是 256 时，它在生成 102400 字节的块时大约重置 100 次。所以，如果状态每 102400 字节自动重置 100 次，并且使用了 100 个不同的种子来加密那个 10 MiB 的文件，那将是 10,000 次内部状态重置……所以，要破解随机数，你需要**破解 AES 超过 10,000 次**……更不用说它实际上是**来自 2 个不同 AES 变换的 XOR**，他实际上并没有检查随机数本身，他实际上会看到在与消息数据进行二进制 XOR 后的随机数……文件本身的大小也放大了这一点，100 MiB 文件，10,000 个种子，1000 MiB 文件，100,000 个种子（一百万倍！！！）。请记住，任何试图“解决”随机数的计算机也必须重现该算法的精确条件；构建表、密钥和计数器扩展、通过 AES 和 SHA256 的传递，这将在每次迭代中涉及数千个处理器周期。

事实上，我今天有时间测试了内部重置与差值的比例（平均 1000 次运行，每次都使用唯一的种子和扩展表种子）

每 102400 块的平均差值/内部状态更改

1024 : 17.6
512 : 43
256 : 94
128 : 191
64 : 388
32 : 770

你可能会想，但如果你能*猜测*一个种子块的 2 个密钥/计数器，你就可以得到哈希值，然后构建下一个密钥/计数器，然后滚动通过该块……但是记得扩展表吗？啊……没有用于构建该随机化表的 48 字节密钥，你就无法获得下一个密钥和计数器的正确哈希值，看到了吗，它们是如何联系在一起的？

现在我知道下一个问题是什么，“是的，但是吞吐量呢？” 诚然，分辨率调得很高，但 AES 非常快……我可以在我的 amd 四核上用 CSRG 以此分辨率创建 100 MiB 的随机数据，大约需要 24 秒，加上文件写入和一次额外的 XOR，你仍然可以达到大约 200 MiB/分钟，考虑到它能提供的安全性，这非常合理。但我可能会调低它，在构建大小中添加一个 0，并将重新播种模数（类中的“Differential”属性）提高到 512，这可能会使吞吐量几乎翻倍（我必须测试一下，并权衡取舍……）。

如果此过程产生的数据足够随机（并且所有统计测试都表明如此），那么破解随机数所需的计算能力（这将是解密任何与该随机数进行 XOR 的数据的必要步骤）将涉及巨大的计算量，远超目前和可预见的未来计算系统的能力。我在这里提出的想法本质上是一个创建加密器的配方，在所有实际意义上，它都可以创建无懈可击的加密。一个使用确定性机器创建的一次性密码（One Time Pad）。

到目前为止，这是我能构建的一个好的 xor 密码，但我知道它可以改进，并且我绝对欢迎任何关于如何使其更好的建议（我认为 SHA 是此实现中的“薄弱环节”，只有两次表运行在 64 字节、块和最终化器上……扩展方法可以做得更具打白性）。所以，如果你知道更好的方法，一种可以改进这些方法或任何其他方法的方式，请说出来，我听着……

那么，为什么需要如此多的安全性？我认为 AES 被破解了吗？怀疑，如果我这么认为就不会用它了……我是否认为可能存在某种方法可以“引导”针对 AES 的暴力破解？也许，如果不行，你可以打赌有人现在正在努力。但目前，破解一个 256 位密钥，特别是如果使用了 CBC 模式，几乎是不可能的……但有些人认为量子计算可能会改变这一切……

我在这里着手要做的是为一次性密码（One Time Pad）实现创建一个引擎。消除暴力破解攻击破解随机数的可能性，并且，如果使用 AES 计数器实现向输出引入了离散模式，通过创建短状态变化周期来缓解这些模式。我还认为，让状态变化变得不规则会减少任何模式的可见性，并且结合 2 个变换，以及密钥交换之间的重叠，以及由此导致的字节信息损失，将使任何模式更加模糊。

这不是我的第一个实现，我还尝试过将 AES 变换与 Camellia 和 Twofish 进行异或，但两者都有复杂的密钥扩展例程，所以速度真的很慢，这在“必须快速”的标准方面是最好的。我将那些实验留在了 LokiOld.cs 类中，以防你想自己玩玩。

CSRG API

构造函数
publicCSRG()
加载默认表种子。

publicCSRG(byte[] TableSeed)
加载用户定义的表种子。必须是 48 字节的随机数。

属性
public EngineModesEngine
选择引擎类型：Dual 或 Single AES CTR。

public intOutputMaximum
单次种子输出的最大字节数。

public intSeedSize
所需的种子缓冲区大小。

public DifferentialsStateDifferential
更改混乱的重新播种差值。值越小，重新播种越积极。

方法
public byte[] Generate(Int32Size,byte[] Seed)
使用属性定义的参数生成随机字节块。
Size：返回数据的字节大小。
Seed：随机种子，固定大小：必须为 64 字节长。
Returns：data byte[]

public byte[] Generate(Int32Size,byte[] Seed,EngineModesEngine)
生成随机字节块。
Size：返回数据的字节大小。
Seed：随机种子，固定大小：必须为 64 字节长。
Engine：AES 引擎类型，单 CTR，或双异或 CTR。
Returns：data byte[]

public byte[] Generate(Int32Size,byte[] Seed,EngineModesEngine,DifferentialsDifferential)
生成随机字节块。
Size：返回数据的字节大小。
Seed：随机种子，固定大小：必须为 64 字节长。
Engine：AES 引擎类型，单 CTR，或双异或 CTR。
Differential：重新播种模数差值。值越小，重新播种越多。
Returns：data byte[]

SHA256

SHA256 现在完全内联到 CSRG 类中，作为一个优化的方法，仅在块大小边界（64 字节）上进行哈希。这是我的设计标准之一，类中没有 Microsoft 加密 API。它仍然是 SHA256，是 bouncycastle 实现的重写，但内部方法 ComputeHash64() 现在是一个具有固定输入大小的内部方法。我确实在项目中包含了完整的类 SHA256Digest。

SHA256Digest API

SHA256Digest 类是 bouncycastle 类的重写，使其成为一个独立的类，并进行了一些优化和重构。输出已针对安全哈希标准文档中的标准进行了测试。我添加了一个 ComputeHash 方法以使其与 Windows 实现对齐，并为该类添加了一个 Dispose 机制。CSRG.cs 类中包含一个具有固定 64 字节输入大小的更紧凑的方法。SHA256Digest 类位于本项目“Experiments”文件夹中。

public voidBlockUpdate(byte[] Input,intInputOffset,intLength)
如果为文件或大型输出流生成哈希值时使用。处理完所有数据后，调用 DoFinal 以检索哈希值。传递给此方法的输入块必须是块对齐的，长度正好为 64 字节。
Input - 要处理的字节。
InputOffset - Input 中的起始位置。
Length - 要处理的数据长度。

public byte[] ComputeHash(byte[] Input)
单次调用方法（如 Windows 实现中所用）。输入要进行哈希处理的字节。
Input - 要处理的字节。
Returns - byte[] 值哈希。

public Int32DoFinal(byte[] Output,Int32OutputOffset)
当使用 BlockUpdate() 方法时，这是在处理完数据后调用的最后一个方法，它可以包含任何大小作为 Output。然后 Output 被更改为哈希值本身。
Output - 要处理的最后一个数据块，变为字节形式的哈希返回值。
OutputOffset - Output 数组中的起始位置。
Returns - 已处理的字节。

public voidReset()
重置算法的内部状态。

public voidUpdate(byteInput)
使用单个字节更新消息摘要。
Input - 要处理的一个字节数据。

public voidDispose()
释放内部变量。在类将被销毁时调用。

内部 AES 实现

CSRG.cs 类中的高级加密标准 (AES) 方法是一个单向加密器，具有固定的 256 位密钥大小。它已被优化为仅执行给定参数所必需的最少计算次数。它基于 mono library 中使用的知名实现，而我认为后者又是使用 Novell 实现创建的。两个主要方法是 Transform，它加密 16 字节数据块，以及 ExpandKey，它将 32 字节密钥扩展为 60 个成员的 UInt32 数组。输出已针对 NIST 发布的 AES 标准文档中的规范测试进行了测试（如果你想更好地理解 AES，这是一个很好的阅读材料）。

私有的 voidTransform(byte[] InData,byte[] OutData,UInt32[] Key)

私有的 UInt32[] ExpandKey(byte[] Key)

NIST 统计测试套件

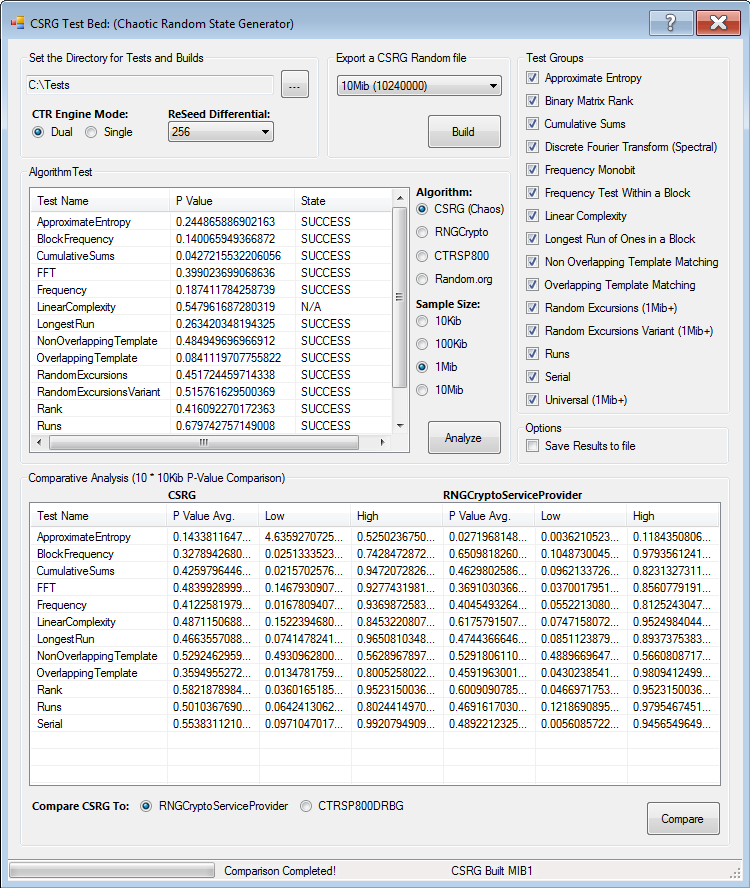
好吧，我该说什么呢，我只是厌倦了在命令行中工作，一次只做一个测试，所以我把 NIST 统计测试套件做成了一个库；添加了导出，注释掉了 fprint，并在 utilities 中编写了几个默认方法（但我没有改变任何计算内容！）。所以现在，你可以使用 PInvoke 将它作为一个 C 库来运行。所有 api 都在 NistSTS.cs 类中，并且都进行了很好的注释。

原始的 NIST 统计测试套件命令行应用程序可在此处获得，手册可在此处获得。非常感谢这个伟大工具的作者，该应用程序内部的代码非常令人印象深刻，非常值得一看……

NIST 测试套件是评估伪随机生成器熵最权威的测试套件之一，就统计测试而言，它非常彻底，并且在加密社区中享有盛誉（它得到了 NIST 的批准，他们定义了美国的加密标准）。所以，这笔交易不错（这花了大量的精力！）。我构建了一个漂亮的小测试平台，它可以将 CSGR 与 RngCrypto、bouncycastle 的 CTRSP800DRBG（我将其从 java 转换为 C#，并尽可能少地更改以使其正常工作，主要只是注释掉 TDEA 部分）进行比较。它还可以从 random.org 获取真正的随机数据，以便你建立一个基线（但每天有 1MB 的免费随机数据限制！）。显然，他们的数据来自接收大气噪声的广播塔。

所以，如果你运行测试，你会发现 CSRG 一致通过，并且 P 值都在良好范围内（大多数接近 0.5，除了两个频率测试在 0.6-0.8 之间更好，最长运行的长度你争取在 0.2 左右，近似熵应该也稍低一些，比如 0.1-0.3 是最好的）。我在帮助文件中添加了手册的摘录，以便你更好地了解输入建议和结果预期，如果你想要更多，请阅读手册。你会注意到很多 P 值的波动（来自所有生成器，甚至 random.org），这是正常的，你需要运行数千次测试才能建立趋势（只记住；成功=好，失败=坏……）。一些测试只能在较大的样本上运行（1 MiB 或更多），否则它们会抛出 OUT OF RANGE 异常，这就是为什么在选择更大的尺寸之前禁用这些测试。

除了线性复杂度测试（没有通过分数，始终评为 N/A）之外，你还会看到每个测试的 SUCCESS 或 FAIL 以及计算出的 P 值。现在，看到偶尔的 FAIL 是正常的，即使是原始随机数据也会出现这种情况。同时也要记住，样本量越大，值就越有可能收敛到它们的统计平均值，所以更大的构建会更准确地读取生成器的输出熵水平。如果你看到大量的失败，或成组的失败，或某个测试持续失败，那么就该回到原点了；o)

我注意到所有基于 AES CTR 的生成器在某些测试中似乎都有一些偏差（就像 SHA/G、BBS 和所有其他生成器在其他测试中一样），并且你执行的测试越多，结果中的趋势就越明显，这表明了特定算法的弱点。总的来说，我不得不说 CSRG 的测试结果非常好，至少和所有我测试过的 CTR 生成器一样好，并且它满足或超过了我对该项目的所有标准，所以，我可能会最终在我的 xor 密码中使用它的一个变体……

该测试的重点是 M 位块中最长一的运行。该测试的目的是确定所测试序列中最长一的运行长度是否与随机序列中预期最长一的运行长度一致。请注意，预期最长一的运行长度的任何不规则性都意味着预期最长零的运行长度也存在不规则性。因此，只需要对一进行测试。

结论和结果解释

对于第 2.4.8 节中的示例，由于 P 值 ≥ 0.01（P 值为 0.180609），结论是序列是随机的。请注意，大的 χ2(obs) 值表明所测试序列中存在一的簇。

输入大小建议

建议每个要测试的序列至少包含第 2.4.2 节表中指定的位数。

返回：P 值。

二进制矩阵秩测试

测试目的

重叠模板匹配测试的重点是预指定目标字符串的出现次数。此测试和第 2.7 节的非重叠模板匹配测试都使用一个 m 位窗口来搜索一个特定的 m 位模式。与第 2.7 节的测试一样，如果未找到模式，则窗口滑动一个比特位置。此测试与第 2.7 节的测试之间的区别在于，当找到模式时，窗口仅滑动一个比特然后恢复搜索。

结果解释

由于第 2.8.4 节步骤 4 中获得的 P 值 ≥ 0.01（P 值为 0.274932），结论是序列是随机的。请注意，对于 2 位模板（B = 11），如果整个序列中有过多的 2 位一的运行，那么：1) ν5 会过大，2) 测试统计量会过大，3) P 值会很小（< 0.01），4) 会得出非随机的结论。

输入大小建议

K、M 和 N 的值已选择，使得每个要测试的序列至少包含 10^6 位（即 n ≥ 10^6）。可以选择各种 m 值，但目前，NIST 建议 m=9 或 m = 10。如果需要其他值，请按如下方式选择：

n ≥ MN。

N 应选择为 N • (min πi) > 5。

如果 P 值 < 0.01，这将表明 Ti 的观察频率计数存储在 νI bin 中的值与预期值不同；预期 Ti 的频率分布（在 νI bin 中）应与计算出的 πi 成正比。

输入大小建议

选择 n ≥ 10^6。M 值必须在 500≤ M ≤ 5000 的范围内，并且 N ≥ 200 才能使 χ2 结果有效。

参数 M：块大小，默认为 512。
返回：P 值。

串行测试

public static extern doubleNistSerial(intM);

该测试的重点是整个序列中所有可能的重叠 m 位模式的频率。该测试的目的是确定 2^m 个重叠模式的出现次数是否与随机序列的预期大致相同。随机序列具有均匀性；也就是说，每个 m 位模式出现的几率与其他任何 m 位模式相同。请注意，对于 m = 1，串行测试等同于第 2.1 节的频率测试。

结果解释

由于第 2.11.4 节步骤 5 中获得的 P 值 ≥ 0.01（P 值 1 = 0.808792 且 P 值 2 = 0.670320），结论是序列是随机的。请注意，如果 ∇2ψ2m 或 ∇ψ2m 很大，则意味着 m 位块的非均匀性。

输入大小建议

选择 m 和 n，使得 m < log2 n - 2。

参数 M：块大小，默认为 16。
返回：P 值。

测试

要测试 DRBG，你需要一些东西进行比较，以了解什么是好的数字。嗯，我们有 RNGCrypto，至少在 C# 中是这样，但没有多少其他的……NIST 文档 80090A 中提出了一个大纲，从中产生了几个 C 和 Java 版本。Bouncycastle 的 Java 版本包括类 CTRSP800DRBG，我已将其重新制作成 C# 版本用于这些测试（现在你有了 2 个 C# 中的 Drbg！）。

CTRSP800 和 RngCrypto 在我在 Diehard、Ent 和 Nist 统计测试套件中运行的所有测试中都产生了出色的随机分数，所以它们似乎都是好的随机数生成器（但请记住，为了正确评估哪种算法提供最好的熵，你必须测试数千个样本才能平滑小的波动）。我已经将 CSRG 的输出通过 NIST 的测试进行了数千次，使用了从 10 KiB 到 100 MiB 的各种大小，并且它始终以出色的结果通过。考虑到我对项目的标准，最佳选择是 CSRG，因为重新播种机制的复杂性以及内部状态变化的固有不可预测性，它几乎不可能被破解，同时仍然以良好的速度返回出色的随机输出。我还在测试它，但现在正在减少测试，因为结果保持恒定并在我为输出测试建立的指标范围内。

现在是不可避免的免责声明：尽管我仔细研究了所有这些，并且它是基于一种公认的生成加密安全伪随机数的方法（AES CTR），但我不是密码学家，所以请自行承担风险。在任何新算法被接受并广泛使用之前，都需要进行大量测试，请记住这一点，自己进行测试，弄清楚它是如何工作的，然后做出明智的选择。

我不是以密码学家的身份来处理这个项目的，而是以工程师的身份，因此我将其分解为一系列需要解决的逻辑问题，我认为结果是一个巧妙的设计，并且具有潜力。总之，如果你有关于改进设计的任何想法，请给我发电子邮件，如果你有问题，请发表评论……

干杯

更新

约翰，你为什么要做这么多更新？好的，好的！我想我这次终于完成了……玩得开心（7 月 20 日）

7 月 14 日 - 将“Loki”算法重命名为 CSRG，清理了代码。

7 月 19 日 - 添加了包含 NIST STS 库的新测试平台，添加了一个新测试平台，以及一个具有扩展属性和方法选项的第二个生成器方法。

7 月 20 日 - 扩展了文章，包含 api 定义，删除了旧内容。扩展了帮助文件以包含 CSRG api 定义。可能是最后一次更新……

7 月 24 日 - 添加了熵池和扩展表旋转方法。将 DUAL 种子大小增加到 96 字节。将推荐的块大小提高到 100 KiB。