归并排序

• 下载 Merge_sort.rar - 482 B
• 下载 Merge_sort.zip - 509 B

引言

归并排序是一种分治排序技术，我们将整个数组分成几个部分，然后对它们应用归并技术，然后将它们组合起来以产生最终的排序数组。归并排序由两个基本算法组成，称为MERGE和MERGE_SORT。

背景

基本算法MERGE是将两个已排序的数组组合成一个新的已排序数组的过程。

就像说有两个数组，

现在我们将对其应用MERGE技术。

1. 首先，我们将创建一个大小为m+n的新数组，其中m是Arr1的大小，n是Arr2的大小。就像在这种情况下，m=4且n=4。因此，我们的新数组Arr3的大小将是4+4=8。                                                 
2. 现在我们将有两个指针，一个指向Arr1的第一个位置，另一个指向Arr2的第一个位置。
3. 然后它们开始比较这两个指针的值。值较小的指针将该值复制到Arr3中，并向右移动一位。
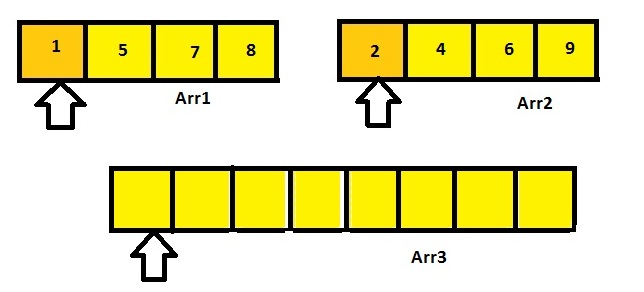
4. 现在，对于第一次比较，Arr1[0]=1且Arr2[0]=2。因此，由于1<2，所以Arr3[0]=1，Arr1[0]处的指针递增，现在指向Arr1[1]。
5. 同样，现在Arr1[1]=5且Arr2[0]=2。我们知道2<5，因此Arr3[1]=Arr2[0]=2。指向Arr2[0]的指针递增，现在指向Arr2[1]。
6. 同样，现在Arr1[1]=5且Arr2[1]=4。我们知道4<5，因此Arr3[2]=Arr2[1]=4。指向Arr2[1]的指针递增，现在指向Arr2[2]。
7. 类似地，经过几个步骤后，我们得到，

它实际上比较了两个数组的元素，并选择较小的元素，并将其添加到新数组中。

通过这种方式，两个数组被合并成一个新的排序数组。

MERGE的算法是，

MERGE ( A, low1, high1, low2, high2 )

1. while low1<=high1 and low2<=high2 then
   1. if A[low1] > A[low2] then B[i++] = A[low2++]
   2. else if A[low1] < a[low2] then B[i++] = A[low1++]
   3. else
      1. B[i++] = A[low1++]
      2. B[i++] = A[low2++]
   4. End while
2. while low1 <= high1
   1. B[i++] = A[low1++]
   2. End while
3. while low2 <= high2
   1. B[i++] = A[low2++];
   2. End while
4. for j = low upto j<i 
   1. A[low++] = B[j]
   2. Increment j by 1
5. End MERGE

然后是归并排序算法。它实际上将给定的数组分割成最小的大小，然后通过MERGE将数组合并到排序的新列表中。

MERGE_SORT( A, low, high )

1. if low < high then
   1. mid = ( low+high )/2
   2. MERGE_SORT( A, low, mid )
   3. MERGE_SORT( A, mid+1, high )-
   4. MERGE( A, low, mid, mid+1, high )
2. END MERGE_SORT

例如，

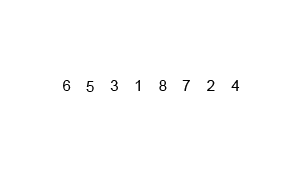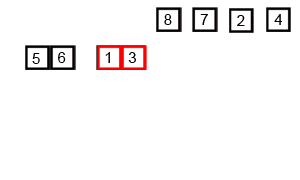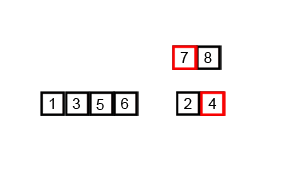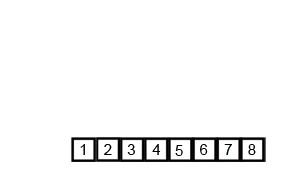
排序的工作流程图是

现在考虑一个MERGE_SORT(A,1,6)。表示对一个包含6个元素的数组进行归并排序，索引从1到6。

此递归算法中的控制流程是，

在时间复杂度的情况下，

在MERGE()算法中，我们将n（假设）个数组1的元素复制到数组3，将m（假设）个数组2的元素复制到数组3

所以复杂度是O(n+m)，可以认为是O(n)

所以合并两个排序数组的复杂度是O(n)

MERGE_SORT( A, low, high )----------------------------------->T(n)

1. if low < high then
   1. mid = ( low+high )/2
   2. MERGE_SORT( A, low, mid )----------------------->T(n/2)
   3. MERGE_SORT( A, mid+1, high )------------------->T(n/2)
   4. MERGE( A, low, mid, mid+1, high )---------------->O(n)

所以方程是T(n)=2*T(n/2)+O(n) 

使用主定理，（通过这个检查 http://en.wikipedia.org/wiki/Master_theorem ）

T(n)=O(nlogn)

代码

这是使用C的归并排序的标准形式之一

#include<stdio.h>
void merge(int arr1[],int ll1,int ul1,int ll2,int ul2)
{
    int i=0,k,ll=ll1;
    int arr3[100];
    while(ll1<=ul1&&ll2<=ul2)
    {
        if(arr1[ll1]<arr1[ll2])
            arr3[i++]=arr1[ll1++];
        else
            arr3[i++]=arr1[ll2++];
    }
    while(ll1<=ul1)
        arr3[i++]=arr1[ll1++];
    while(ll2<=ul2)
        arr3[i++]=arr1[ll2++];
    for(k=0;k<i;k++)
        arr1[ll++]=arr3[k];
}
void merge_sort(int arr1[],int ll,int ul)
{
    int mid;
      if(ll<ul)
   {
          mid=(ul+ll)/2;
        merge_sort(arr1,ll,mid);
        merge_sort(arr1,mid+1,ul);
        merge(arr1,ll,mid,mid+1,ul);
   }
}
void main()
{
    int arr1[100];
    int n,i;
    printf("\nEnter the no. of elements present in the array :");
    scanf("%d",&n);
    for(i=0;i<n;i++)
    {
        printf("\narr[%d]=",i);
        scanf("%d",&arr1[i]);
    }
    merge_sort(arr1,0,n-1);
    printf("\nThe sorted array is...");
    for(i=0;i<n;i++)
    {
        printf("\narr[%d]=%d",i,arr1[i]);
    }
}

结论

这是归并排序的标准描述。它是一种分治排序方法。归并排序是一种排序，其最佳，最差和平均情况的时间复杂度相同。 

参考

1. Introduction to Algorithms by CORMEN, LEISERSON, RIVEST, STEIN
2. www.wikipedia.org ( the moving picture and the url is taken from wikipedia )