八皇后问题：树算法

• 下载 EightQueens.zip - 8.8 KB

引言

“八皇后问题是指在8×8的国际象棋棋盘上放置八个皇后，使得任意两个皇后都不能相互攻击。

这个问题在计算上可能相当复杂，因为在8×8的棋盘上有4,426,165,368种可能的摆放方式，但只有92个解。”（维基百科）

我们能否用一个简单的树形算法解决这个问题（对于八皇后和N皇后）？

如果可以，在C#中它看起来是什么样的？

背景

Code Project 上有几篇关于这个主题的文章（例如这里，这里，这里，这里，这里，这里，以及这里）。但对我来说，没有一篇真正清晰简洁。而且我认为，例如这个“示例程序”已经非常过时了。所以在这里，我将一步一步地解释一个有效的树形算法及其在C#中的实现。

树形算法

我们从一个空的棋盘开始，尝试将第一个皇后放置在第一行的任何一个格子上。我们有八种可能的选择（从a8到h8），但是一旦我们选择了一个选项，第二行中放置第二个皇后的可能格子就会减少，第三行中可能减少得更多。

那么，让我们假设第一个皇后放置在第一行（正常棋盘上的第8行）的c8位置。

之后，我们在第二行中放置第二个皇后有五种可能性：a7、e7、f7、g7和h7。

在这里，我们选择g7。

现在，我们在第三行中放置第三个皇后有两种可能性：b6和d6。

依此类推。

在这个例子中，我们找到了一个有效的解决方案：从第8行到第1行，皇后的位置分别是c、g、b、h、f、d、a和e。

因此，我们可以将从第一行到最后一行的决策路径表示为一个决策树，其中包含可能的节点和已选择的节点：

这看起来并不太复杂。选项的数量似乎随着行数而迅速减少！所以我们的方法看起来很有希望，不是吗？如果我们幸运的话，这里的可能性会比44亿少得多。

那么，让我们来实现这个算法并运行它来遍历所有树路径——然后我们来分析结果。

C# 实现

我们从一个非常简单的 `Position` 类开始。它只有一个 `line`、一个 `row` 和一个 `parent`。当然，它提供了一个递归方法用于遍历树（`WalkThroughTree`）。

public class Position
{
    private int line, row;
    private Position parent;

    public Position(int Line, int Row, Position Parent)
    {
        line = Line;
        row = Row;
        parent = Parent;
    }

    public void WalkThroughTree()
    {
        if (line == NumberOfQueens) // last line (=number of queens) reached: solution
        {
            PrintSolution(this); // print solution
            return;
        }
        for (var r = 0; r < NumberOfQueens; r++) // try all rows in next line
        {
            // check threats for all queens in previous lines

            // ...

            if (queenAbove.line == 0) // no threat found
                new Position(line + 1, r, this).WalkThroughTree(); // put queen on next line
        }
    }
}

基本上就是这样。我们可以从我们的（虚拟的）根节点开始——位于第0行，棋盘上没有有效的位置——然后生成整个树。

new Position(0, Int32.MinValue, null).WalkThroughTree();

当然，每当我们尝试在下一行的某个位置放置一个新的皇后时，我们必须在真正将其放置在新位置之前检查该位置是否安全。

在这个例子中，a6不安全，b6安全，c6不安全。我们通过简单地比较下一个皇后的列与每个先前皇后的列来检查威胁。如果列号相等，我们就找到了一个垂直威胁（例如，c8威胁c6）；如果它们之间的差等于它们行号之间的差，我们就找到了一个对角线威胁（例如，c8威胁a6）。因此，对于每次威胁检查，我们只需要从上面的 `WalkThroughTree` 中进行很少的比较。

for (var r = 0; r < NumberOfQueens; r++) // try all rows in next line
{
    // check threats for all queens in previous lines
    var queenAbove = this;
    while (queenAbove.row >= 0 && r != queenAbove.row // vertical threat?
           && r - queenAbove.row != line + 1 - queenAbove.line // diagonal threat left?
           && queenAbove.row - r != line + 1 - queenAbove.line) // diagonal threat right?
        queenAbove = queenAbove.parent; // repeat check for all queens in previous lines
    if (queenAbove.line == 0) // no threat found
        new Position(line + 1, r, this).WalkThroughTree(); // put queen on next line
}

此外，我们可能会找到少于八个皇后的解决方案。因此，我们只在尝试中确实识别出足够数量的皇后时才打印解决方案（`PrintSolution`）——参见上面的“`if (line == NumberOfQueens)`”。

private static void PrintSolution(Position Node)
{
    NumberOfSolutions++;
    while (Node.row >= 0)
    {
        Console.Write(((char)('a' + Node.row)).ToString());
        Node = Node.parent;
    }
    Console.WriteLine();
}

通过这个 `PrintSolution` 方法，我们简单地将每个成功决策路径的所有列逐个打印到控制台。结果如下：

在这里，您可以看到上面我们的示例解决方案被突出显示为我们解决方案列表中的一个结果（从第8行到第1行的皇后位于c、g、b、h、f、d、a和e列）。

如果我们还添加一些计数器，我们可以看到：有15,720次尝试，总共有（仅仅）2,056个节点（不包括虚拟根节点），并且确实有92个解决方案。

我的旧电脑处理所有这些解决方案需要3毫秒。数字与理论相符：“回溯深度优先搜索程序是置换方法的轻微改进，它一次考虑棋盘的一行来构建搜索树，从而在构建早期阶段就消除了大多数非解棋盘位置。由于它即使在不完整的棋盘上也拒绝了车和斜线攻击，因此它只检查了15,720种可能的皇后放置方式”（维基百科）。

N皇后

我们也可以轻松地更改棋盘大小和皇后数量。

public static int NumberOfQueens = 8; // n queens

对于7皇后，我在2毫秒内得到40个解决方案。

对于12皇后，我在400毫秒内得到14,200个解决方案。

对于13皇后，我在2400毫秒内得到73,712个解决方案。

对于14皇后，我在9秒内得到365,596个解决方案（树中有27,358,552个节点，尝试在安全位置放置皇后的次数为377,901,398次）。

我们可以再次将这些结果与维基百科进行比较。它们是吻合的。

关注点

起初，我将子节点也存储在节点中。但最终事实证明，这种基于简单递归的遍历方式并不需要存储子节点。

我还发现有趣的是，C#能够如此快速地处理大约2700万个树节点和近3.78亿次基于树的比较（例如，在14皇后问题的情况下）。人脑也非常快。但它通常处理大约50个节点（7 x 7）。

此外，我还将整个程序翻译成了C++和Java。然后我比较了性能结果。

C++ (CLR) - 8,723 毫秒

Java - 8,788 毫秒

C# - 8,618 毫秒

我还比较了更多标准。

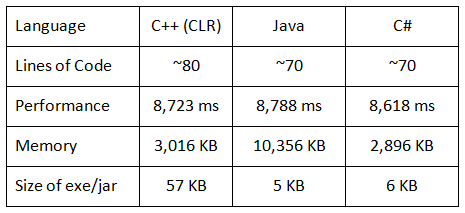
对我来说，这是一个令人惊讶的结果：C#全部胜出。

历史

2014年8月11日 - 发布。

2014年8月12日 - 增强了性能和解释，并优化了源代码。

2014年8月13日 - 添加了与C++的比较。