统计工作台
4.99/5 (66投票s)
使用统计分布探索您的数据:使用完全基于反射的应用程序,探索、初始化、创建、估计和使用Accord.NET框架中的统计分布。

目录
引言
统计学一直是我着迷的学科。对某些人来说,它可能不为人所知,但人工智能、机器学习,甚至“数据挖掘”、“深度学习”和“商业智能”等热门话题的大多数现代和近期发现,往往只是传统统计学的简单应用。有些应用无疑是深思熟虑和精心的,但大多数实际上可以被视为涉及几个统计分布的简单应用数学。
在本文中,我们将看到如何使用Accord.NET框架的统计模块来创建概率分布,根据数据估计这些分布,并了解如何从现有分布生成新的数据样本。最后,我们将看到如何将所有这些操作组合到一个单一的应用程序中,用于教学、可视化和处理这些分布。
背景
统计学中最重要的概念之一是概率分布的概念。概率分布使我们能够应对现实世界中观测(测量)的不确定性。它们可以告诉我们所观测变量的不同值是如何分布的——获取这些信息在多种情况下都很有用。
其中一个原因是,处理概率分布通常比处理观测本身更容易。例如,如果我们确定(或只是假设)一个变量遵循可以用数学公式定义的特定分布,我们就可以将正在分析的数据与公式本身互换。这意味着,我们不必将数据加载到内存中并进行计算,而是可以在纸上写下描述数据的公式,然后通过代数运算获得答案,而无需执行任何数字运算。
好的,那么概率分布如何让我们应对不确定性呢?为了弄清楚这一点,让我们看一个例子。
示例假设我们是一家小型家庭式枫糖浆生产工厂的骄傲主人。在我们的工厂里,有一台机器负责将大约100毫升的枫糖浆灌装到每个瓶子里。然而,我们知道这台机器有时会少装一点,有时会多装一点,这取决于它当天的心情。

在给定的例子中,每个瓶子中枫糖浆的精确量是不确定的,因为我们无法准确确定机器会向每个瓶子中倒入多少糖浆。然而,这并不能阻止我们尝试根据我们能观察到的机器行为来建模。
因此,让我们将机器可能倒入瓶中的糖浆量表示为**X**。现在,请注意,当我们实际观察机器工作时,**X**可能被观察到是95毫升、98毫升、100毫升,或实数线上的任何其他正值。每次我们启动机器时,**X**的观测值都会改变。因此,这意味着我们无法为这个X找到一个唯一且确定值(因为它随每次观测而变化);但我们可以找到这个变量的观测值可能落在*特定范围*内的概率。
现在,我们如何表达与**X**相关的不同范围和概率?嗯,第一步是了解X是什么。这个X不是一个普通的变量,而是一个*随机*变量。之所以称之为随机,是因为它随每次观测而变化,但请不要误解:仅仅因为称之为随机,并不意味着这个变量不遵循某些规则。实际上,情况恰恰相反:这个变量是随机的,因为它有一个附加的**概率分布**——一个将不同概率分配给这个变量可以假设的不同值范围的机制。
从枫糖浆到概率分布
用一个非常简单的解释来说,概率分布可以表示为一个函数,该函数给出随机变量X给定范围的概率(一个介于0和1之间的值)。这个函数被称为概率分布函数。它可以用来回答以下问题:
X在a和b之间的概率是多少?- P(a <
X≤ b) 的概率是多少? [读作X落在a和b之间的概率] - P(
X≤ 100) 的概率是多少? [读作X小于或等于100的概率] - P(
X> 100) = p 中的 p 值是多少?
或者更实际地说
- 机器灌装瓶子容量在0毫升到100毫升之间的概率是多少?
- 机器灌装瓶子容量小于100毫升的概率是多少?
注意:表达分布函数最常见的形式是写 P(X ≤ x),意思是“观察到的X小于或等于x的概率”。然而,它也可以同样地表示为 P(X > x),表示“观察到的X大于x的概率”;或者,以更一般的形式 P(a < X ≤ b),意思是“观察到的X在a和b之间”。当a或b被省略时,表示我们应该考虑变量可能值的下限或上限。
现在,概率分布可以通过多种方式定义。最常见的是通过累积分布函数 (CDF) 或概率密度函数 (PDF) 来指定,后者积分后得到分布函数。从这两个公式中,我们可以获得关于分布的多种度量和辅助函数。这些度量包括分布的均值、中位数、众数、方差和范围值。其他函数包括分位数函数(逆分布)、互补分布函数、分位数密度函数和风险函数。
因此,我们看到所有概率分布都有共同的主要属性和主要函数。在这种情况下,尝试使用编码器熟悉的通用概念——类*接口*——来建模概率分布的概念可能很有趣。

图 1. 概率的通用接口
Accord.NET 框架中的分布
既然我们有了概率分布的接口,那么各个分布会是什么样子呢?
这完全取决于我们打算采取哪种方法。处理统计数据主要有两种方法:*参数*方法和*非参数*方法。在这两种方法中,仍然可以计算大部分相同的度量,如前所述。然而,最流行的方法可能仍然是参数方法(我们很快就会发现原因)。
在参数方法中,我们假设分布函数遵循特定的数学公式,其中缺少一些参数。例如,让我们考虑正态分布。正态分布的密度函数和分布函数可以分别表示为
$f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{\frac{-(x-\mu)^2}{2\sigma^2}}$
$F(x) = \int_{-\infty}^x f(x) dx .$
请注意,这些函数实际上只接受一个参数 (x),但其组成中还有另外两个变量。它们是均值 (\(\mu\)) 和标准差 (\(\sigma\))。两者都被认为是分布的参数,并且必须在这些公式可以使用之前指定。现在,优点是两者都可以通过一些简单的计算,只需对我们可能拥有的数据进行一次遍历,就能非常容易地获得。我们首先计算我们值的均值 (\(\mu\)),然后计算标准差或值 (\(\sigma\))。然后将它们代入上述公式。
如我们所见,这种简单性是参数方法的最大优点。需要估计的参数很少。更重要的是,
它们的计算可以手工进行。
现在,很容易低估这句话的重要性。但请记住,在不久之前,曾有一段时间计算机实际上是人类。
然而,通过指定不同的参数化和不同的公式,我们可以创建几种*标准*概率分布(或分布族),用于对我们的数据进行建模。例如,下图显示了其中一些分布以及它们如何应用于相同的*概率分布接口*。

图 2. 不同分布如何适应同一接口的示例。
好的,那有什么诀窍?
我的朋友,诀窍在于,如果我们为数据选择了错误的分布,那么我们基于这个错误分布所做的任何进一步计算或操作都将毫无意义。
这是参数统计的最大问题。虽然理论分布具有有用的分析特性,但这并不意味着我们使用的数据实际上会遵循这些特性。因此,我们必须仔细选择应该为我们的数据假设哪种分布,并且我们必须确保我们估计的参数确实是我们现有数据的良好估计。
那么我们可以选择哪些分布呢?我们如何知道它们与我们现有数据的关系如何?
统计工作台
进入**统计工作台**。工作台是一个用于发现、探索和学习不同统计分布的应用程序。它还可以用于将分布拟合到您的数据并建议您在假设中可以使用的最合适的分布。

统计工作台中正态分布的概述。
该应用程序是完全交互式的。浏览某个特定分布时,您可以更改其参数并立即查看分布属性和函数如何受到影响。
现在,一个很酷的地方是该应用程序完全基于反射。该应用程序检查Accord.NET 框架中实现的所有概率分布,以填充其接口。它甚至查询文档文件以构建您在上面看到的描述页面。
回到枫树
为了展示该应用程序的实用性,我们将在工作台上解决一个示例问题。这个示例与之前完全相同,但增加了额外的趣味性。
示例假设我们是一家小型家庭式枫糖浆生产工厂的骄傲主人。在我们的工厂里,有一台机器负责将大约100毫升的枫糖浆灌装到每个瓶子里。然而,我们知道这台机器有时会少装一点,有时会多装一点,这取决于它当天的心情。
尽管这台老旧的机器有点脾气,但最近生意一直很好。好到一家超市连锁店对转售我们的枫叶产品很感兴趣。然而,为了确保质量和消费者满意度,超市规定我们的产品不能少于瓶子上宣传的糖浆量。为了遵守现行法规,不符合规格的瓶子数量不得超过交货量的5%。
在给定的例子中,每个瓶子中枫糖浆的精确量是不确定的,因为我们无法准确确定机器会向每个瓶子中倒入多少糖浆。然而,我们知道机器更有可能生产某些范围的体积而不是其他范围,我们可以利用这个事实来做出明智的决定,从而相应地调整生产。
那么,让我们启动工作台

让我们转到“估计”选项卡


现在,让我们观察一下让机器工作时会发生什么。首先,我们将机器配置为每个瓶子倒入100毫升。然后我们拿了一些量杯,观察机器运行100次,每次记录机器实际倒入量杯中的枫糖浆量。我们将所有结果汇总在一个Excel电子表格中,该表格实际上随工作台应用程序一起提供。点击“估计”选项卡顶部的“打开文件”按钮,您就可以在那里看到它

让我们打开它,然后点击上面的“估计”按钮

如您所见,有时机器生产的量少于100毫升,有时多于100毫升。估计分析也告诉我们,正态分布与中间列表中其他备选方案相比是一个不错的选择。然而,它并没有告诉我们这毕竟是一个好的假设。
但在这种情况下,我们还有另一个优势。事实证明,正态分布也称为“误差的正态分布”。关键是,每次机器将液体倒入瓶中时,过程中都可能存在许多误差来源。例如,注射喷嘴可能短暂堵塞,枫糖浆的稠度波动,计数喷嘴停止时间的传感器不够精确,等等。
这个过程中的每一步都可能增加一点误差,这些误差会累积并最终表现为我们得到的最终误差。所有这些因素的累加使得机器每个瓶子倒入95毫升、98毫升或105毫升,而不是100毫升。现在,好的方面是,当多个误差源加在一起时,每个误差源都有自己的未知分布,这些误差的总和趋向于正态分布。为了验证这一点,请观看**Quincux机器**——也称为高尔顿板——的工作原理
好的,太棒了。那么我们继续使用正态分布。从估计的分布来看,即使我们的机器设置为倒入100毫升,平均也倒入99.77毫升(非常接近),标准差为2.32。
好的。但是,这种标准差在实际中究竟意味着什么?
让我们切换到“分析”选项卡来了解。在分析选项卡中,我们可以看到机器生产的不同体积。看来大多数瓶子的容量最终在95毫升到105毫升之间。那么让我们检查一下目前我们的机器灌装少于100毫升的瓶子的概率是多少

根据正态分布,我们的机器生产的瓶子中,少于100毫升的概率似乎超过50%,这显然不是一个好兆头。请记住,我们必须只生产少于5%的瓶子,且容量少于100毫升。那我们该怎么办呢?好吧,让我们通过调整分布来检查我们目前生产的最差的5%的瓶子。

根据分布,目前生产的瓶子中有5%只装了95.95毫升。现在,让我们重新定位我们的分布,使得这最差的5%正好发生在我们的100毫升目标之前

太好了!所以事实证明,如果我们把机器设定为生产104毫升而不是100毫升,我们只会生产5%以内的不合格瓶子。这样我们既能满足超市的要求,又*不会在其他瓶子上浪费资源*。
既然我们有了新的分布参数,让我们生成一些新样本,看看机器调整后我们可以预期什么样的体积。

如所见,生成列表中低于100的值的预期数量应小于5。
它是如何工作的?
最酷的部分是上面展示的应用程序**完全基于反射**。统计工作台本身对每个不同的分布一无所知。相反,它利用反射来列出和检查*Accord.NET框架中实现的所有概率分布*以进行操作。即使应用程序中显示的文档页面也实际上是从框架附带的IntelliSense文档中提取的。
Accord.NET 框架
Accord.NET框架是一个.NET机器学习框架,结合了音频和图像处理库。它完全用C#编写,可用于任何.NET应用程序,包括WinForms、WPF、Windows Store,甚至Android和iOS(通过Xamarin和Shim)。它是一个完整的框架,用于构建生产级计算机视觉、计算机听觉、信号处理和统计应用程序,可免费**和**商用。
由于大多数研究领域或多或少地使用统计学,因此该框架的统计模块是迄今为止开发最完善的模块之一。截至本文撰写之时,该框架提供了50种单变量连续分布、9种单变量离散分布、8种多变量连续分布和3种多变量离散分布。当前的分布列表包括
该框架还可以仅根据用户提供的定义CDF、PDF或两者兼有的 lambda 函数来创建功能完备的分布实现。该框架可以*通过数值优化从给定函数自动计算所有必要的度量和函数,仅从用户指定的单个 lambda 函数即可提供众数、中位数、期望值、风险函数、分位数函数等*。例如:
该框架还包括假设检验,您可以用来检验关于数据的各种假设,例如它属于哪种分布,我们是否应该相信其估计参数等等。然而,这可能是另一篇文章的内容。
目前,工作台仅支持并显示单变量分布。然而,如上所述,该框架提供的远不止这些。分布的命名空间分为Accord.Statistics.Distributions.Univariate和Accord.Statistics.Distributions.Multivariate。单变量分布实现了IUnivariateDistribution接口,而多变量分布实现了IMultivariateDistribution。两者都派生自最通用的IDistribution接口,该接口基本上只指定了所有分布必须实现的CDF和PDF方法。

图 3. Accord.NET 框架中多变量和单变量分布的接口。
现在,这些又进一步分为连续或离散实现。对于每一个,都有一个基类,为与概率分布相关的各种功能提供默认方法。例如,如果我们要实现一个新的连续分布,并且只指定其CDF和PDF函数,继承自UnivariateContinuousDistribution将为我们提供查找分布中位数和默认InverseDistributionFunction的默认实现。然后,我们可以在新分布中使用中位数和ICDF,而无需实际实现它们。

图 4. 连续和离散单变量分布的基类。注意只有均值、
方差、支撑集以及分布函数和密度/质量函数需要
由基类指定(它们以斜体显示,表示它们是抽象方法)。指定
这5个项目后,所有其他项目立即可用,例如分位数函数、
中位数,以及**从分布生成新样本**。
其参数可以从数据中估计的分布实现了IFittableDistribution接口。该接口提供了一个通用的Fit方法,其参数类型与分布期望的观测值类型匹配。例如,NormalDistribution期望其观测值为双精度数,因此实现了IFittableDistribution<double>。同样,离散的泊松分布期望其观测值为整数,因此实现了IFittableDistribution<int>。
一些分布还可以根据其参数的估计方式采用特殊选项。在这种情况下,接口还允许一个额外的参数,用于指定它支持哪些选项。选项在选项对象中定义,例如NormalOptions。
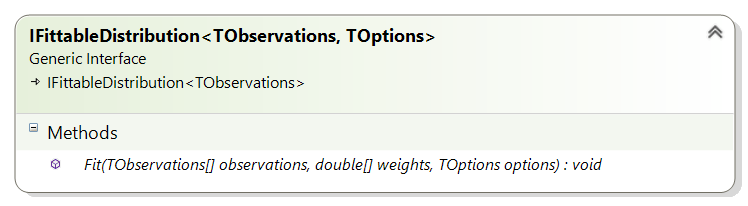
图5. IFittableDistribution 接口。此方法可以传递
观测值来调用,分布应尝试拟合这些观测值,以及每个
观测值的个体权重和任何应使用的特殊拟合选项(如果有)。
该框架还有一些特殊的分布,它们实际上旨在与其他分布结合使用。例如Mixture<T>分布、MultivariateMixture<T>、Independent和Independent<T>。这些可以实例化为Mixture<NormalDistribution>、Mixture<BernoulliDistribution>、MultivariateMixture<MultivariateNormalDistribution>、Independent<NormalDistribution>等等。下面我们看几个框架如何使用的示例,并将最后这些留作更高级的案例。
使用代码
实例化新的概率分布
假设在我们的应用程序中,我们需要创建一个具有特定均值和标准差的正态(高斯)分布。为此,我们首先将框架的命名空间导入到我们的源文件中
using Accord.Statistics;
using Accord.Statistics.Distributions.Univariate;
之后,让我们创建一个均值μ=4,标准差σ=4.2的正态分布。
// Create a new Normal distribution with mu: 4 and s: 4.2
var normal = new NormalDistribution(mean: 4, stdDev: 4.2);
现在我们可以根据需要查询分布的任何属性
double mean = normal.Mean; // 4.0 (mu)
double median = normal.Median; // 4.0 (for the Gaussian, same as the mean)
double mode = normal.Mode; // 4.0 (for the Gaussian, same as the mean)
double stdDev = normal.StandardDeviation; // 4.2 (sigma)
double var = normal.Variance; // 17.64 (sigma squared)
我们还可以查询其相关函数
// The cumulative distribution function, or the probability that a real-valued
// random variable will be found to have a value less than or equal to some x:
double cdf = normal.DistributionFunction(x: 1.4); // 0.26794249453351904
// The probability density function, or the relative likelihood for a real-valued
// random variable will be found to take on a given specific value of x:
double pdf = normal.ProbabilityDensityFunction(x: 1.4); // 0.078423391448155175
// The log of the probability density function, useful for applications where
// precision is critical
double lpdf = normal.LogProbabilityDensityFunction(x: 1.4); // -2.5456330358182586
// The complementary distribution function, or the tail function, that gives the
// probability that a real-valued random variable will be found to have a value
// greater than some x. This function is also known as the Survival function.
double ccdf = normal.ComplementaryDistributionFunction(x: 1.4); // 0.732057505466481
// The inverse distribution function, or the Quantile function, that is able to
// revert probability values back to the real value that produces that probability
double icdf = normal.InverseDistributionFunction(p: cdf); // 1.4
// The Hazard function, or the failure rate, the event rate at time t conditional
// on survival until time t or later. Note that this function may only make sense
// when using time-defined distributions, such as the Poisson.
double hf = normal.HazardFunction(x: 1.4); // 0.10712736480747137
// The cumulative hazard function, that gives how much the hazard
// function accumulated over time until a given time instant x.
double chf = normal.CumulativeHazardFunction(x: 1.4); // 0.31189620872601354
// Every distribution has a friendly string representation
string str = normal.ToString(); // N(x; mu = 4, s2 = 17.64)
请注意,这些函数和度量是通用IDistribution接口的一部分。因此,无论我们创建什么分布,用法始终相同。例如,让我们将正态分布切换为离散的泊松分布
// Create a new Poisson distribution with lambda = 0.7
PoissonDistribution poisson = new PoissonDistribution(0.7);
double mean = poisson.Mean; // 0.7 (lambda)
double median = poisson.Median; // 1.0
double mode = poisson.Mode; // 0.7 (lambda)
double stdDev = poisson.StandardDeviation; // 0.836 [sqrt((lambda))]
double var = poisson.Variance; // 0.7 (lambda)
// The cumulative distribution function, or the probability that a real-valued
// random variable will be found to have a value less than or equal to some x:
double cdf = poisson.DistributionFunction(k: 1); // 0.84419501644539618
// The probability density function, or the relative likelihood for a real-valued
// random variable will be found to take on a given specific value of x:
double pdf = poisson.ProbabilityMassFunction(k: 1); // 0.34760971265398666
// The log of the probability density function, useful for applications where
// precision is critical
double lpdf = poisson.LogProbabilityMassFunction(k: 1); // -1.0566749439387324
// The complementary distribution function, or the tail function, that gives the
// probability that a real-valued random variable will be found to have a value
// greater than some x. This function is also known as the Survival function.
double ccdf = poisson.ComplementaryDistributionFunction(k: 1); // 0.15580498355460382
// The inverse distribution function, or the Quantile function, that is able to
// revert probability values back to the real value that produces that probability
int icdf = poisson.InverseDistributionFunction(p: cdf); // 1
// The Hazard function, or the failure rate, the event rate at time t conditional
// on survival until time t or later. Note that this function may only make sense
// when using time-defined distributions, such as the Poisson.
double hf = poisson.HazardFunction(x: 1); // 2.2310564445595058
// The cumulative hazard function, that gives how much the hazard
// function accumulated over time until a given time instant x.
double chf = poisson.CumulativeHazardFunction(x: 1); // 1.8591501591854034
// Every distribution has a friendly string representation
string str = poisson.ToString(); // Poisson(x; lambda = 0.7)
我们也可以用同样的方法创建多维分布。在下一个例子中,我们来看看如何创建多维高斯分布并计算它的一些度量。
// Create a multivariate Gaussian distribution
var dist = new MultivariateNormalDistribution
(
// mean vector mu
mean: new double[] { 4, 2 },
// covariance matrix sigma
covariance: new double[,]
{
{ 0.3, 0.1 },
{ 0.1, 0.7 }
}
);
// Common measures
double[] mean = dist.Mean; // { 4, 2 }
double[] median = dist.Median; // { 4, 2 }
double[] mode = dist.Mode; // { 4, 2 }
double[,] cov = dist.Covariance; // { { 0.3, 0.1 }, { 0.1, 0.7 } }
double[] var = dist.Variance; // { 0.3, 0.7 } (diagonal from cov)
int dimensions = dist.Dimension; // 2
// Probability density functions
double pdf1 = dist.ProbabilityDensityFunction(2, 5); // 0.000000018917884164743237
double pdf2 = dist.ProbabilityDensityFunction(4, 2); // 0.35588127170858852
double pdf3 = dist.ProbabilityDensityFunction(3, 7); // 0.000000000036520107734505265
double lpdf = dist.LogProbabilityDensityFunction(3, 7); // -24.033158110192296
// Cumulative distribution function (for up to two dimensions)
double cdf = dist.DistributionFunction(3, 5); // 0.033944035782101534
double ccdf = dist.ComplementaryDistributionFunction(3, 5); // 0.00016755510356109232
从数据值估计分布
可能出现的情况是,我们不想使用均值和标准差的具体值,而是想直接从一组值中估计正态分布。例如,假设我们有以下值:
// Suppose those are our observed values
double[] observations = { 0.10, 0.40, 2.00, 2.00 };
// Now, in order to fit a distribution to those values,
// all we have to do is to create a base distribution:
var normal = new NormalDistribution();
// and then pass those values to its .Fit method:
normal.Fit(observations);
// Result is N(x; 1.125, 1.017)
string text = normal.ToString()
现在,假设我们的一些样本实际上比其他样本更重要。它们中的一些具有更大的*权重*。在这种情况下,我们可以为每个观测值指定一个实数值,表示每个特定观测值相对于其他观测值的权重。然后,我们可以将观测值和权重这两个向量传递给分布拟合过程,如下所示。
// Suppose those are our observed values and their individual weights
double[] observations = { 0.10, 0.40, 2.00, 2.00 };
double[] weights = { 0.25, 0.25, 0.25, 0.25 };
// We create a base distribution:
var normal = new NormalDistribution();
// and then pass the values and weights to its .Fit method:
normal.Fit(observations, weights);
// Result is N(x; 1.125, 1.017)
string text = normal.ToString()
下面的示例展示了如何将一个多维高斯分布拟合到一组观测值。不幸的是,这些观测值是线性相关的,导致协方差矩阵是非正定的。为了解决这个问题,我们传递了一个拟合选项对象,指定应该以稳健的方式进行估计。
// Suppose we would like to fit a multidimensional Normal distribution to
// those samples. Those samples are linearly dependent between themselves,
// and attempting to fit them directly might result in an exception.
double[][] observations =
{
new double[] { 1, 2 },
new double[] { 2, 4 },
new double[] { 3, 6 },
new double[] { 4, 8 }
};
// Create a base distribution with two dimensions
var normal = new MultivariateNormalDistribution(2);
// Fit the distribution to the data
normal.Fit(observations, new NormalOptions()
{
Robust = true // do a robust estimation
});
从现有分布生成新样本
可以从框架中的*任何*单变量分布生成新样本。有些分布具有比其他分布更快的专门样本生成方法,但所有分布都可以进行采样,无论是通过专门方法还是使用默认的分位数函数方法。
以下示例展示了如何从均值为2,标准差为5的正态分布中生成1000000个样本。
// Create a Normal with mean 2 and sigma 5
var normal = new NormalDistribution(2, 5);
// Generate 1000000 samples from it
double[] samples = normal.Generate(1000000);
// Try to estimate a new Normal distribution from the
// generated samples to check if they indeed match
var actual = NormalDistribution.Estimate(samples);
string result = actual.ToString("N2"); // N(x; mu = 2.01, s2 = 25.03)
以下示例展示了如何从试验次数为4、成功概率为0.2的二项分布中生成1000000个样本。
// Create a Binomial with n = 4 and p = 0.2
var binomial = new BinomialDistribution(4, 0.2);
// Generate 1000000 samples from it
double[] samples = target.Generate(1000000).ToDouble();
// Try to estimate a new Binomial distribution from
// generated samples to check if they indeed match
var actual = new BinomialDistribution(4);
actual.Fit(samples);
string result = actual.ToString("N2"); // Binomial(x; n = 4.00, p = 0.20)
以下示例展示了如何从均值向量为[2, 6],协方差矩阵为[2 1; 1 5]的多元正态分布中生成1000000个样本。
// mean vector
double[] mu = { 2.0, 6.0 };
// covariance
double[,] cov =
{
{ 2, 1 },
{ 1, 5 }
};
// Create a multivariate Normal distribution
var normal = new MultivariateNormalDistribution(mu, cov);
// Generate 1000000 samples from it
double[][] samples = normal.Generate(1000000);
// Try to estimate a new Normal distribution from
// generated samples to check if they indeed match
var actual = MultivariateNormalDistribution.Estimate(samples);
在Accord.NET框架中,有两种创建新概率分布的方法:使用Lambda函数或使用继承。虽然后者是创建新分布的首选方法,因为它更容易在不同类和项目之间共享这些分布,但当我们需要尽快测试某些东西时,使用Lambda函数可能更容易编写快速而粗糙的代码。
使用Lambda函数
要使用lambda函数创建新分布,我们可以使用GeneralContinuousDistribution类。这个类可以基于定义所需分布的CDF、PDF或两者兼有的lambda函数来创建新分布。
// Let's suppose we have a formula that defines a probability distribution
// but we dont know much else about it. We don't know the form of its cumulative
// distribution function, for example. We would then like to know more about
// it, such as the underlying distribution's moments, characteristics, and
// properties.
// Let's suppose the formula we have is this one:
double mu = 5;
double sigma = 4.2;
Func<double, double> df = x =>
1.0 / (sigma * Math.Sqrt(2 * Math.PI)) * Math.Exp(-Math.Pow(x - mu, 2) / (2 * sigma * sigma));
// And for the moment, let's also pretend we don't know it is actually the
// p.d.f. of a Gaussian distribution with mean 5 and std. deviation of 4.2.
// So, let's create a distribution based _solely_ on the formula we have:
var distribution = GeneralContinuousDistribution.FromDensityFunction(df);
// Now, we can check everything that we can know about it:
double mean = distribution.Mean; // 5
double median = distribution.Median; // 5
double var = distribution.Variance; // 17.64
double mode = distribution.Mode; // 5
double cdf = distribution.DistributionFunction(x: 1.4); // 0.19568296915377595
double pdf = distribution.ProbabilityDensityFunction(x: 1.4); // 0.065784567984404935
double lpdf = distribution.LogProbabilityDensityFunction(x: 1.4); // -2.7213699972695058
double ccdf = distribution.ComplementaryDistributionFunction(x: 1.4); // 0.80431703084622408
double icdf = distribution.InverseDistributionFunction(p: cdf); // 1.3999999997024655
double hf = distribution.HazardFunction(x: 1.4); // 0.081789351041333558
double chf = distribution.CumulativeHazardFunction(x: 1.4); // 0.21776177055276186
使用继承
要使用继承创建新分布,首先需要知道您想创建哪种类型的分布。您需要创建一个新类,然后选择以下类之一进行继承:UnivariateContinuousDistribution、UnivariateDiscreteDistribution、MultivariateContinuousDistribution或MultivariateDiscreteDistribution。一旦您知道要选择哪个基类,请实现该类所需的所有虚方法。
例如,假设我们要实现维基百科中给出的Rademacher分布。
namespace MyApplicationNamespace
{
class RademacherDistribution
{
}
}
根据维基百科的描述,它写道:“在概率论和统计学中,拉德马赫分布(以汉斯·拉德马赫命名)是一种离散的概率分布,其中随机变量X有50%的几率是+1或-1。[1]”
由于这是一个离散概率分布,现在我们知道我们需要继承自UnivariateDiscreteDistribution。所以让我们这样做,右键单击类名,并实现其所有虚方法
class RademacherDistribution : UnivariateDiscreteDistribution
{
public override double Mean
{
get { throw new NotImplementedException(); }
}
public override double Variance
{
get { throw new NotImplementedException(); }
}
public override double Entropy
{
get { throw new NotImplementedException(); }
}
public override AForge.IntRange Support
{
get { throw new NotImplementedException(); }
}
public override double DistributionFunction(int k)
{
throw new NotImplementedException();
}
public override double ProbabilityMassFunction(int k)
{
throw new NotImplementedException();
}
public override string ToString(string format, IFormatProvider formatProvider)
{
throw new NotImplementedException();
}
public override object Clone()
{
throw new NotImplementedException();
}
}
现在,我们所要做的就是填写那些缺失的字段
class RademacherDistribution : UnivariateDiscreteDistribution
{
public override double Mean
{
get { return 0; }
}
public override double Variance
{
get { return 1; }
}
public override double Entropy
{
get { return System.Math.Log(2); }
}
public override AForge.IntRange Support
{
get { return new AForge.IntRange(-1, +1); }
}
public override double DistributionFunction(int k)
{
if (k < -1) return 0;
if (k >= 1) return 1;
return 0.5;
}
public override double ProbabilityMassFunction(int k)
{
if (k == -1) return 0.5;
if (k == +1) return 0.5;
return 0.0;
}
public override string ToString(string format, IFormatProvider formatProvider)
{
return "Rademacher(x)";
}
public override object Clone()
{
return new RademacherDistribution();
}
}
分布创建完成后,我们甚至可以查询我们未实现的功能,例如其逆分布函数、风险函数等。
var dist = new RademacherDistribution();
double median = dist.Median; // 0
double mode = dist.Mode; // 0
double lpdf = dist.LogProbabilityMassFunction(k: -1); // -0.69314718055994529
double ccdf = dist.ComplementaryDistributionFunction(k: 1); // 0.0
int icdf1 = dist.InverseDistributionFunction(p: 0); // -1
int icdf2 = dist.InverseDistributionFunction(p: 1); // +1
double hf = dist.HazardFunction(x: 0); // 0.0
double chf = dist.CumulativeHazardFunction(x: 0); // 0.69314718055994529
string str = dist.ToString(); // Rademacher(x)
猜测数据的合理分布
// Create a new distribution, such as a Poisson
var poisson = new PoissonDistribution(lambda: 0.42);
// Draw enough samples from it
double[] samples = poisson.Generate(1000000).ToDouble();
// Let's pretend we don't know from which distribution
// those sample come from, and create an analysis object
// to check it for us:
var analysis = new DistributionAnalysis(samples);
// Compute the analysis
analysis.Compute();
// Get the most likely distribution (first)
var mostLikely = analysis.GoodnessOfFit[0];
// The result should be Poisson(x; lambda = 0.420961)
var result = mostLikely.Distribution.ToString();
如您所见,该框架能够正确猜测样本来自泊松分布。
更高级的示例
混合分布
以下示例展示了如何创建任意数量分量分布的混合分布。
// Create a new mixture containing two Normal distributions
Mixture<NormalDistribution> mix = new Mixture<NormalDistribution>(
new NormalDistribution(2, 1), new NormalDistribution(5, 1));
// Common measures
double mean = mix.Mean; // 3.5
double median = mix.Median; // 3.4999998506015895
double var = mix.Variance; // 3.25
// Cumulative distribution functions
double cdf = mix.DistributionFunction(x: 4.2); // 0.59897597553494908
double ccdf = mix.ComplementaryDistributionFunction(x: 4.2); // 0.40102402446505092
// Probability mass functions
double pmf1 = mix.ProbabilityDensityFunction(x: 1.2); // 0.14499174984363708
double pmf2 = mix.ProbabilityDensityFunction(x: 2.3); // 0.19590437513747333
double pmf3 = mix.ProbabilityDensityFunction(x: 3.7); // 0.13270883471234715
double lpmf = mix.LogProbabilityDensityFunction(x: 4.2); // -1.8165661905848629
// Quantile function
double icdf1 = mix.InverseDistributionFunction(p: 0.17); // 1.5866611690305095
double icdf2 = mix.InverseDistributionFunction(p: 0.46); // 3.1968506765456883
double icdf3 = mix.InverseDistributionFunction(p: 0.87); // 5.6437596300843076
// Hazard (failure rate) functions
double hf = mix.HazardFunction(x: 4.2); // 0.40541978256972522
double chf = mix.CumulativeHazardFunction(x: 4.2); // 0.91373394208601633
// String representation:
// Mixture(x; 0.5 * N(x; mu; = 5, s2 = 1) + 0.5 * N(x; mu = 5, s2 = 1))
string str = mix.ToString(CultureInfo.InvariantCulture);
下一个示例展示了如何直接从数据中估计一个混合分布。
var samples1 = new NormalDistribution(mean: -2, stdDev: 1).Generate(100000);
var samples2 = new NormalDistribution(mean: +4, stdDev: 1).Generate(100000);
// Mix the samples from both distributions
var samples = samples1.Concatenate(samples2);
// Create a new mixture distribution with two Normal components
var mixture = new Mixture<NormalDistribution>(
new NormalDistribution(-1),
new NormalDistribution(+1));
// Estimate the distribution
mixture.Fit(samples);
var a = mixture.Components[0].ToString("N2"); // N(x; mu = -2.00, s2 = 1.00)
var b = mixture.Components[1].ToString("N2"); // N(x; mu = 4.00, s2 = 1.02)
高斯混合模型
以下示例展示了如何创建多元高斯混合模型,以及如何将它们转换为多元正态混合。
// Observations
double[][] samples =
{
new double[] { 0, 1 },
new double[] { 1, 2 },
new double[] { 1, 1 },
new double[] { 0, 7 },
new double[] { 1, 1 },
new double[] { 6, 2 },
new double[] { 6, 5 },
new double[] { 5, 1 },
new double[] { 7, 1 },
new double[] { 5, 1 }
};
// Create a new Gaussian mixture with 2 components
var gmm = new GaussianMixtureModel(components: 2);
// Compute the model (estimate)
double error = gmm.Compute(samples);
// Classify the first samples (they should belong to the same class)
int c0 = gmm.Gaussians.Nearest(samples[0]);
int c1 = gmm.Gaussians.Nearest(samples[1]);
// Classify the last samples (they should belong to the other class)
int c7 = gmm.Gaussians.Nearest(samples[7]);
int c8 = gmm.Gaussians.Nearest(samples[8]);
// Extract the multivariate Normal distribution from it
MultivariateMixture<MultivariateNormalDistribution> mixture =
gmm.ToMixtureDistribution();
独立与联合分布
以下示例展示了如何通过假设数据的每个维度都受不相关的单变量分布支配来创建多元分布。
// Observations
double[][] samples =
{
new double[] { 0, 1 },
new double[] { 1, 2 },
new double[] { 1, 1 },
new double[] { 0, 7 },
new double[] { 1, 1 },
new double[] { 6, 2 },
new double[] { 6, 5 },
new double[] { 5, 1 },
new double[] { 7, 1 },
new double[] { 5, 1 }
};
// Create a new 2D independent Normal distribution
var independent = new Independent<NormalDistribution>(
new NormalDistribution(), new NormalDistribution());
// Estimate it!
independent.Fit(samples);
var a = independent.Components[0].ToString("N2"); // N(x1; mu = 3.20, s2 = 7.96)
var b = independent.Components[1].ToString("N2"); // N(x2; mu = 2.20, s2 = 4.40)
在离散情况下,这可以用联合分布来表示。
非参数分布
以下示例展示了如何从样本本身创建非参数分布,而不假定分布形状的特定形式。这些分布包括经验分布、多元经验分布和经验风险分布。
// Observations
double[] samples = { 5, 5, 1, 4, 1, 2, 2, 3, 3, 3, 4, 3, 3, 3, 4, 3, 2, 3 };
// Create a new non-parametric Empirical distribution
var distribution = new EmpiricalDistribution(samples);
double mean = distribution.Mean; // 3
double median = distribution.Median; // 2.9999993064186787
double var = distribution.Variance; // 1.2941176470588236
double mode = distribution.Mode; // 3
double chf = distribution.CumulativeHazardFunction(x: 4.2); // 2.1972245773362191
double cdf = distribution.DistributionFunction(x: 4.2); // 0.88888888888888884
double pdf = distribution.ProbabilityDensityFunction(x: 4.2); // 0.181456280142802
double lpdf = distribution.LogProbabilityDensityFunction(x: 4.2); // -1.7067405350495708
double hf = distribution.HazardFunction(x: 4.2); // 1.6331065212852196
double ccdf = distribution.ComplementaryDistributionFunction(x: 4.2); //0.11111111111111116
double icdf = distribution.InverseDistributionFunction(p: cdf); // 4.1999999999999993
double smoothing = distribution.Smoothing; // 0.67595864392399474
string str = distribution.ToString(); // Fn(x; S)
或者在多变量情况下,使用核
// Suppose we have the following data, and we would
// like to estimate a distribution from this data
double[][] samples =
{
new double[] { 0, 1 },
new double[] { 1, 2 },
new double[] { 5, 1 },
new double[] { 7, 1 },
new double[] { 6, 1 },
new double[] { 5, 7 },
new double[] { 2, 1 },
};
// Start by specifying a density kernel
IDensityKernel kernel = new EpanechnikovKernel(dimension: 2);
// Create a multivariate Empirical distribution from the samples
var dist = new MultivariateEmpiricalDistribution(kernel, samples);
// Common measures
double[] mean = dist.Mean; // { 3.71, 2.00 }
double[] median = dist.Median; // { 3.71, 2.00 }
double[] var = dist.Variance; // { 7.23, 5.00 } (diagonal from cov)
double[,] cov = dist.Covariance; // { { 7.23, 0.83 }, { 0.83, 5.00 } }
// Probability mass functions
double pdf1 = dist.ProbabilityDensityFunction(new double[] { 2, 1 }); // 0.039131176997318849
double pdf2 = dist.ProbabilityDensityFunction(new double[] { 4, 2 }); // 0.010212109770266639
double pdf3 = dist.ProbabilityDensityFunction(new double[] { 5, 7 }); // 0.02891906722705221
double lpdf = dist.LogProbabilityDensityFunction(new double[] { 5, 7 }); // -3.5432541357714742
最后说明
在结束本文之前,我想再介绍一下Accord.NET 框架的历史及其起源。
从大学早期开始,我就或多或少地从事统计学工作。大学时,我开始研究神经网络;硕士期间,我研究支持向量机、隐马尔可夫模型和隐条件随机场。为了从事这些工作,我学习了数据预处理、数据转换、投影、特征提取、统计学、信息论、数学、图像处理、数学优化、机器学习以及其他一些领域。
从这段经历中,我得以看到统计学在我所经历的几乎所有领域中都扮演着至关重要的角色。因此,为了准确理解我所从事的一切,从一开始我就以我所能找到的最优方式组织我的学习和所积累的知识。事实是,我的记忆力很差,我知道做笔记、画图或摆满一架子书根本行不通。我需要一种方法来存储我所学到的知识,以便我能快速检索。以一种即使是细节也能快速准确地涵盖的方式,并且在一个未来的我无论身在何处都能找到和研究的地方。
我发现最理想的方法就是**用代码**来编写所有获得的知识。多年来,这个过程创建了一个软件框架,拥有在线文档,其中包含我当时阅读的文献的链接,以及注释清晰的源代码,这些代码足够简单,以便我可以在几分钟内刷新我的记忆。通过将其开源并在公共仓库中提供,我可以从任何地方阅读它。通过在宽松许可下共享,我可以在几分钟内发现并纠正错误。几年后,Accord.NET框架就这样诞生了。
如果您有兴趣在.NET中构建自己的机器学习、统计和图像处理应用程序,请花几分钟时间查看该框架已能为您做什么。安装框架非常简单:在Visual Studio中,找到框架的NuGet包并将其添加到您的项目中。在命令窗口中,输入
PM> Install-Package Accord.MachineLearning
这就是让框架启动并运行所需的一切。
结论
在本文中,我们讨论了统计学,并展示了一个可以帮助学生和用户探索和理解统计学如何应用于实际问题的应用程序。我们展示了一个使用Accord.NET框架创建的WPF应用程序,它可以教授、示例、实例化和估计多种单变量统计分布。
最后,我们展示了如何使用Accord.NET框架的统计模块通过代码实现所有这些相同的功能,并提供了几个实现示例。
历史
- 2015年5月16日:第一版发布。
- 2015年5月18日:纠正了一个二进制打包问题。
参考文献
- Christopher M. Bishop (2006), 模式识别与机器学习 (信息科学与统计)。Springer-Verlag New York, Inc., Secaucus, NJ, USA。
- 塔勒布,纳西姆·尼古拉斯 (2007),黑天鹅:高度不可能事件的影响,兰登书屋。
- Hastie, T.; Tibshirani, R. & Friedman, J. (2001), 统计学习的要素, Springer New York Inc. , New York, NY, USA。
- Hollander, M, & Wolfe, D (1999), 非参数统计方法,第2版。Wiley。


