65.9K
CodeProject 正在变化。 阅读更多。
Home

二阶 Goertzel 和 Reinsch 算法

Mosi_62
starIconstarIconstarIconstarIconstarIcon

5.00/5 (4投票s)

2014 年 11 月 11 日

CPOL

6分钟阅读

viewsIcon

25538

downloadIcon

426

Gerald Goertzel 开发了一种非常快速的离散傅里叶变换方法。但似乎很少有描述能真正完整地解释其推导过程。

二阶 Görtzel 算法

网上有很多关于二阶 Goertzel 算法的描述。但大多数都没有完整解释其推导过程。总是有相同的部分缺失。所以我试着填补这个空白。 :)

二阶 Goertzel 算法基于一阶 Goertzel 算法的传递函数

用

将分子和分母乘以 1 + a1 * z^-1 的共轭，使分母变为实数，得到

由此得到差分方程

c[n] + a1 * c[n-1] + c[n-2] = y[n] + b1 * y[n-1]

用

a1 = -2 cos(2kp/N) and b1 = -exp(-j2kp/N)

很长一段时间，我一直在想他们为什么要这样做。差分方程现在看起来复杂得多。但最终还是有一些好处。 :)

在这里，所有的解释现在都说：“既然我们只关心 c[n]，我们可以将复数乘法 b1 * y[n-1] 留到计算最后，并且只在最后执行一次”……这并不完全是事实。我们关心 c[n]，而复数计算可以放在最后。但这两者之间没有联系。我深入研究了数字信号处理的理论才找出原因。 :)

关键在于信号路径。差分方程的信号路径如下所示

如果我们要实现这一点，它将是这样的...

c[n] = y[n] + b1 * y[n-1] - a1 * c[n-1] - c[n-2]

...放入一个循环，在每个周期中，都要进行复数乘法 b1 * x[n-1]，因此，整个计算都必须以复数形式进行。比一阶 Goertzel 算法所需的计算量大得多。这并非我们想要的。

信号路径可以绘制成这样

现在，我们有了两个独立的传递函数，并且这两个函数可以互相切换而不影响最终的传递函数。

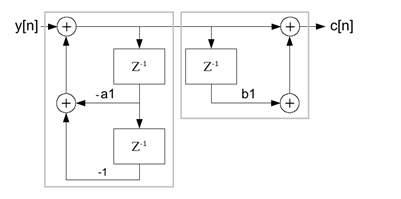
然后重新组合。这种形式称为信号路径的直接形式 II，看起来好得多。反馈部分现在位于函数开头。

将其转化为代码，得到

v[n] = y[n] –a1 * v[n-1] – v[n-2]

对于左侧的反馈部分，

和

c[n] = v[n] + b1 * v[n-1]

对于右侧的前馈部分。

这就是最大的好处。相当复杂的差分方程，只需更改信号路径的绘制方式，就能得到一个非常简短且快速的算法。数学和纯粹的数字信号处理理论的令人印象深刻的交互（而完成这一切的人，Gerald Goertzel，确实令人钦佩？）

反馈部分必须在一个遍历 y 的所有样本的循环中实现。这意味着从 0 到 N-1。

    for (n = 0; n < N; n++)
    {
        v0.real = y[n].real - a1.real * v1.real - v2.real;
        v2 = v1;
        v1 = v0;
    }

我使用了复数数据类型，因为最终我们得到的是复数。

右侧部分只需要在计算结束时计算一次（这与我们只查找 c[n] 无关？）。基本上，右侧部分包含复数乘法 v[n-1] * b1。到目前为止，我们只处理了实数值。这意味着 v[n-1] 是实数，没有虚部。因此，接下来的复数乘法并不复杂。实部变为 v[n-1].real * b1.real，虚部变为 v[n-1].real * b1.imag。最后，我们寻找傅里叶分量 a[n] = c[n].real*2 和 b[n] = -c[n].imag*2。这两个值都应该计算为 c[n] = v[n] + b1 * v[n-1]。现在对于实部，它是

c[k].real = (v0.real + b1.real * v2.real);

由于 v[n] 是实数值且没有虚部。虚部 c[k].imag 的计算变得稍短

c[k].imag = -(b1.imag * v1.real);

最后，由于以下原因，这两个值都必须除以 N

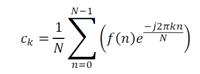
有了这个，所有傅里叶分量 a[0] 到 a[N-1] 和 b[0] 到 b[N-1] 的序列是

for (k = 0; k < N; k++)
{
v0.real = 0;
v0.imag = 0;
v1.real = y[1].real;
v1.imag = y[1].imag;
v2.real = y[0].real;
v2.imag = y[0].imag;
b1.real = -Math.Cos((double)(2.0 * Math.PI * (double)(k) / (double)(N)));
b1.imag = Math.Sin((double)(2.0 * Math.PI * (double)(k) / (double)(N)));
a1.real = -2 * Math.Cos((double)(2.0 * Math.PI * (double)(k) / (double)(N)));
a1.imag = 0;
for (n = 0; n < N; n++)
{
v0.real = y[n].real - a1.real * v1.real - v2.real;
v2 = v1;
v1 = v0;
}
c[k].real = (v0.real + b1.real * v2.real) / (double)(N) * 2.0;
c[k].imag = -(b1.imag * v1.real) / (double)(N) * 2.0;
}

And at the end it takes
c[0].real = c[0].real / 2;
c[0].imag = c[0].imag / 2;

这样实现的话，二阶 Goertzel 算法就是一种非常快速的离散傅里叶变换方法。在我的电脑上，具有 1000 个样本的测试应用程序耗时 8 毫秒。标准的离散傅里叶变换实现需要 120 毫秒才能完成相同的计算。但计算速度的提高是以牺牲一些精度为代价的，而且当样本数量过大时，Goertzel 算法不稳定。即使在我的测试应用程序中，也已经可以看到一些不精确。对于矩形信号，所有实部都应该为 0。但 a[1] = -0.12，a[2] = 0.04，a[3] = -0.11，依此类推。在标准实现中，a[1] = 0.04，a[2] = 0.04，a[3] = 0.04，这是谐波的相位偏移，可能造成很大的差异。

关于稳定性，我读到 Reinsch 算法是二阶 Görtzel 算法的改进版本，并且是稳定的。所以，我也实现了它进行比较。

Reinsch 算法

Reinsch 算法是 Görtzel 算法的修改版。

对于 cos(2Pi*k/N) > 0，Reinsch 取部分

            v[n] = y[n] - a1 * v[n-1] - v[n-2]

并说对于 v[n] – v[n-1] 之间的差值

            v[n] - v[n-1] = y[n] - a1 * v[n-1] - v[n-2] - v[n-1]

他对这个方程进行 +2 * v[n-1] 和 – 2 * v[n-1] 的扩展，由于 a1 = -2cos(2Pi*k/N)，他得到

            v[n] - v[n-1] = y[n] + (2cos(2Pi*k/N) - 2) * v[n-1] + v[n-1] - v[n-2]

现在有两个替换

            (2cos(2Pi*k/N) - 2) = - 4 * sin(Pi*k/N)^2

令 v[n] – v[n-1] = dv[n]，最后的两项 v[n-1] – v[n-2] = dv[n-1]，

我们将得到：

            dv[n] = y[n] - 4 * sin(Pi*k/N)^2* v[n-1] + dv[n-1]

最后得到 v[n]

            v[n] = dv[n] + v[n-1]

这是一个带有 dv[n] 作为反馈部分的循环，看起来像这样

a1.real = - 4 * Math.Pow(Math.Sin((double)(Math.PI * (double)(k) / (double)(N))), 2.0);
a1.imag = 0;
we[k] = a1.real;
for (n = 0; n < N; n++)
{
   dW = y[n].real + a1.real * v1.real + dW;
   v0.real = dW + v1.real;
   v1 = v0;
}
c[k].real = (dW - a1.real / 2.0 * v0.real) / (double)(N) * 2.0;
c[k].imag = (b1.imag * v1.real) / (double)(N) * 2.0;

对于 cos(2Pi*k/N) >= 0，Reinsch 取和而不是差值

            v[n] + v[n-1] = y[n] - a1 * v[n-1] - v[n-2] + v[n-1]

得到

            (2cos(2Pi*k/N) + 2) = 4 * cos(Pi*k/N)^2

和

            v[n] = dv[n] - v[n-1]

这就是像

a1.real = 4 * Math.Pow(Math.Cos((double)(Math.PI * (double)(k) / (double)(N))), 2.0);
a1.imag = 0;
we[k] = a1.real;
for (n = 0; n < N; n++)
{
   dW = y[n].real + a1.real * v1.real - dW;
   v0.real = dW - v1.real;
   v1 = v0;
}
c[k].real = (dW - a1.real / 2.0 * v0.real) / (double)(N) * 2.0;
c[k].imag = (b1.imag * v1.real) / (double)(N) * 2.0;

所以我可以比较这两种算法，结果有点令人失望。

Görtzel 算法的不稳定性是由早期浮点数运算中的数字消隐引起的。如果整个算法都用精度为小数点后 7 位的 float 变量实现，就可能发生这种情况。以这种方式实现，有超过 28000 个样本时，k = 1 的 cos(2Pi*k/N) 变为 1.0。但现在使用双精度值，这种情况就不会再发生。因此，只要 DFT 是在现代 64 位计算机上执行，并且是用 C# 这样的现代语言实现的，这两种算法在多达 100000 个样本时仍然表现相同。这意味着，只要是这样，Reinsch 算法就没有必要了 :-)

二阶 Goertzel 算法是一个非常快速的方法，但它也有其缺点。关于精度，Reinsch 算法也存在同样的问题。我通过将所有使用的 exp(j2k /N) 值的计算放入一个数组并从中提取，对离散傅里叶变换进行了一个稍快的实现。使用该算法，相同的变换运行时间为 20 ms，并且精度与标准实现相同。见

这可能是一个不错的选择。 :-)

然而，二阶 Görtzel 和 Reinsch 算法都是非常复杂的算法，并且都需要大量的数学和计算机科学工作。

© . All rights reserved.