对象跟踪：轻松使用粒子滤波器

查看源代码 下载二进制文件	查看源代码 下载二进制文件
- 点击查看视频
颜色对象跟踪：每个粒子都模拟红色颜色的概率。粒子滤波器用于检测和跟踪红笔。	模板选择：模板的大小、角度和位置由粒子建模。粒子滤波器用于选择更可能的模板子集，从而减少匹配时间。

目录

1. 引言
2. 粒子滤波器
3. 实现
4. 结论
5. 参考文献

引言

NuGet 包：统计学 帮助：离线 - Statistics.ParticleFilter - 下载后取消阻止！

目标跟踪是计算机视觉的主要任务之一。目标跟踪广泛应用于各种应用程序中，例如：视频监控、汽车跟踪（距离估计）、人员检测和跟踪等。目标跟踪器通常需要一些初始化步骤，例如初始目标位置，这可以通过手动或使用 Viola-Jones 检测器或快速模板匹配等目标检测器自动提供。跟踪存在几个主要问题：

• 遮挡
• 多目标
• 尺度、光照、外观变化
• 困难和快速的运动
• ...

尽管目标跟踪问题已经存在多年，但仍未解决，并且存在许多目标跟踪器，有专为特定目的构建的，也有通用的。

卡尔曼滤波器假设线性运动模型和高斯噪声，并且只返回一个假设（例如，被跟踪物体的可能位置）。如果运动快速且不可预测（例如，刮风天树上的叶子），卡尔曼滤波器很可能会失败。粒子滤波器返回多个假设（每个粒子代表一个假设），因此可以处理非高斯噪声并支持非线性模型。除了目标跟踪（其中状态是位置向量 (x, y)）之外，状态可以是任何东西，例如模型的形状。本文将解释粒子滤波器背后的主要思想，并将重点介绍其在目标跟踪中的实际应用以及示例。

粒子滤波器 - 主要思想

粒子滤波器是一种通用函数优化算法，其中解决方案搜索空间通过粒子（采样）进行搜索。那么这意味着什么呢？在我们的例子中，每个粒子都包含测试，以确定对象在粒子所在位置的可能性。在粒子评估完成后，根据粒子的优劣分配权重。然后，通过重采样过程，好的粒子被复制，坏的粒子被移除。下一代粒子接着预测对象可能在哪里。然后对这一代进行评估，循环重复。

与卡尔曼滤波器相反，粒子滤波器可以模拟非线性物体运动，因为运动模型不需要像离散卡尔曼滤波器那样写成状态转移矩阵。此外，粒子滤波器相当容易理解，但也有一个缺点：滤波器的性能取决于粒子数量，粒子数量越多，估计就越好，但成本也越高。尽管如此，粒子滤波器在通用函数优化中被广泛使用，包括目标跟踪。

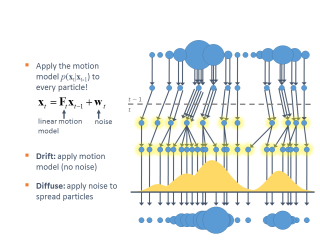
下图显示了粒子滤波器的两个主要步骤。

粒子滤波器的循环。与卡尔曼滤波器相反，粒子滤波器处理一般的概率密度。首先，滤波器从提供的状态转移（例如运动模型）预测下一个状态，然后（如果适用）在校正阶段纳入噪声测量信息。循环重复。
分布表示：假设我们有一些（目前我们不知道的）想要表示的概率密度（红色）。我们可以将其表示为一组（加权）样本。每个蓝色圆圈代表从分布中抽取的一个样本。圆圈半径代表粒子的权重。可以看出，一组加权粒子可以近似一个分布。	分布表示（样本）：粒子数量是粒子滤波器的关键参数。例如，我们希望用粒子表示这种由两个高斯混合组成的分布。将使用蒙特卡罗近似。如果使用足够的粒子，将获得良好的表示。使用的样本是未加权的；如果样本加权，可以获得更好的表示。
粒子：单个粒子也称为样本（参见上图）。这是因为它在目标（后验）分布中的作用（样本）。每个粒子包含 状态估计 - x(t) 相关权重 - w(t) 其中粒子由 n 索引，而 N 是粒子总数。	步骤：我们从之前的估计开始。第一步是粒子重采样和权重归一化（红色）。然后我们对每个粒子应用状态转移（例如运动模型）（绿色）。这两个步骤包含在预测步骤中。更新步骤由测量和权重更新组成。测量使用观测模型进行（金色）。最后，使用观测模型更新粒子的权重，以给出后验分布（红色）。所有步骤构成一个重复的迭代。

预测

预测是第一步，包括根据粒子权重进行粒子选择重采样，下一个状态转移（例如应用运动模型）漂移以及施加噪声扩散。

重采样
1a) 重采样（通用）：第一步是粒子重采样。粒子根据其权重进行重采样，其中权重较高的粒子有更大的机会被选中。同一个粒子可以被多次选中——重复采样。重采样步骤可以比作“自然选择”，最好的样本得以幸存。	1b) 重采样（样本）：我们从上一次迭代的加权粒子开始。重采样从上一个粒子集中抽取新样本。需要重采样步骤以阻止退化。当单个样本具有极度主导的权重时，就会发生退化。粒子重采样后，权重分布设置为均匀分布。
1c) 重采样（退化）：蓝色点代表样本，而红线代表它们近似的分布。如果我们继续根据粒子的权重对其进行加权，权重将累积，好的粒子将继续获得越来越多的权重，而坏的粒子将逐渐减少。最终结果是分布将不再被很好地表示。为了避免这种情况，需要重采样步骤。
漂移和扩散
1a) 漂移和扩散（通用）：首先应用漂移。由于每个粒子在应用漂移（这里是运动模型 F）后具有不同的状态，预测将不同。接下来，施加噪声 w(t) 以覆盖一些不太可能的假设，并使一些相同的粒子稍微分化——重采样步骤。	1b) 漂移和扩散（样本）：这里的漂移操作是运动模型的应用。运动模型单独应用于每个粒子。此运动模型是二维恒定速度运动模型。

更新（修正）

在获得带噪声的测量值后，更新（校正）步骤开始。对每个粒子进行评估，并根据获得的似然更新每个粒子的权重。

2a) 更新（通用）：在获得带噪声的测量值后，根据每个粒子的状态估计评估观测模型（例如直方图相似性）。观测模型模拟了假设我们知道对象的状态 x(t) 时测量值 z(t) 出现的可能性。	2b) 更新（样本）：蓝色圆圈表示由漂移（例如运动模型 x(t)）传播的状态估计粒子。现在，必须使用图像中的数据将状态估计转化为观测值。在这种情况下，图像数据是由粒子状态定义的边界框获得的直方图。此图像显示了由蓝色和橙色框表示的两个估计。由蓝色框定义的估计表示对粉红女孩所在位置的更好猜测。
2c) 更新（样本）：在计算每个状态的直方图距离后，我们可以通过定义的 p(z|x) 更新来更新每个粒子。状态产生与原始直方图相似的粒子将具有更大的权重，而如果直方图与预期模型不匹配，则将获得较低的权重。对每个粒子应用观测模型后，我们现在有了更新的分布！请注意，高权重粒子集中在女孩身上，而低权重粒子则位于外围。	2d) 更新（状态估计）：我们的最后一步是使用更新后的粒子评估状态。可以采用最大似然，但这种方法会产生嘈杂的输出。最常见的方法是粒子状态的中位数或均值。如果使用离散标签，例如，如果状态的一个元素用于标记 3 个人 {1,2,3}，则中位数或均值不适用。

现在您已经了解了基础知识，是时候进行实际示例了，但首先简要介绍一下实现。

实现

粒子滤波器实现为 IEnumerable<TParticle> 或 IList<TParticle> 的一系列扩展方法，其中 TParticle 实现 IParticle 接口。方法实现为在粒子集合（例如粒子滤波器）上定义的扩展。这种实现方式提供了

• 灵活性
• 特定部分的自定义实现
• 可扩展性
• 开发人员学习曲线短

下面的类图显示了实现概要

类图。通用粒子滤波器的实现没有引入任何新类。相反，它将单个粒子实现为一个轻量级接口，并为 ParticleFilter 类中定义的粒子集合（例如粒子滤波器）提供扩展方法。

假设我们想使用恒定速度模型，并且测量模型是对象的位置（正如上图中所示）。该示例的用法如下所示

粒子

粒子实现了两个主要方法：drift 和 diffuse。由于我们不包含任何运动模型，此方法为空。我们通过随机化当前粒子位置来扩散粒子。下面显示的代码省略了一些不重要的实现细节。

class ColorParticle: IParticle
{
    public double Weight { get; set; }
    public PointF Position { get; set; }

    //we do not have velocity (or something else), so nothing :)
    public void Drift()
    { }

    public void Diffuse()
    {
        //randomize the position a little bit
    }
    
    ...
}

初始化

最复杂的步骤是初始化，包括粒子实现（漂移和扩散）和初始化。所示的初始化过程在图像上均匀散射 1000 个粒子。

//ColorParticle is the implementation of the particle of the introductory sample
List<ColorParticle> particleFilter = new List<ColorParticle>();
particleFilter.CreateParticles(1000,  //particles' count
                               ColorParticle.FromArray, //convert arr => position (create from array)
                               new ISampleableDistribution<double>[]  //position range
                               { 
                                    new UniformContinuousDistribution(0, imgSize.Width),
                                    new UniformContinuousDistribution(0, imgSize.Height)
                               });

预测

预测步骤只包含一个方法，如果没有测量值，该方法将重复执行而没有校正方法。它包括重采样、漂移和扩散方法。

private void predict()
{
   particleFilter = particleFilter.Predict();
}

更新（修正）

更新（校正）方法根据其测量值更新粒子的权重。

private void update()
{
    particleFilter.Update(measure);
}

private double measure(ColorParticle p)
{ 
   //get Euclidean distance from the reference color
}

结论

本文介绍了用于目标跟踪问题的离散粒子滤波器及其在 C# 中的实现。粒子滤波器还有更多用途，因为它可作为通用优化问题，如所包含示例之一所示。

源代码和示例代码是 Accord.NET Extensions Framework 的一部分，这是一个主要用于图像处理、对象检测和跟踪的框架，所有这些都打包为流畅的扩展和简单直观的泛型，所以不要忘记看一看 :)

参考文献

[1]	Smith K. "计算机视觉精选主题 - 2D 跟踪 1/2 IJACI" 迄今为止最好的目标跟踪教程 - 本文中使用了一些幻灯片
[2]	Mallikarjuna Rao G. "使用粒子滤波器的视觉目标跟踪：一项调查"

历史

• 2014年1月16日 - 第一个版本发布