65.9K
CodeProject 正在变化。 阅读更多。
Home

对象跟踪：轻松使用卡尔曼滤波器

Darko Jurić
starIconstarIconstarIconstarIcon
emptyStarIcon
starIcon

4.89/5 (32投票s)

2015年1月16日

LGPL3

9分钟阅读

viewsIcon

172619

离散卡尔曼滤波器简要教程，附带 C# 示例

视频图标。 - 点击查看视频
Kalman Filter 2D Kalman Filter Tracking
卡尔曼滤波器轨迹估计： 测量（检测）噪声被设置为一个相对较高的值，但卡尔曼滤波器成功地预测并修正了对象轨迹。 卡尔曼 + Camshift 跟踪： Camshift 用于检测对象，卡尔曼滤波器用于校正和估计对象的轨迹。

目录

  1. 引言
  2. 卡尔曼滤波器
  3. 实现
  4. 结论
  5. 参考文献

引言

计算机视觉的首要任务之一是对象跟踪。对象跟踪广泛应用于各种应用程序中，例如：视频监控、汽车跟踪（距离估计）、人体检测和跟踪等。对象跟踪器通常需要一些初始化步骤，例如初始对象位置，这可以通过手动或使用对象检测器（如 Viola 和 Jones 检测器或快速模板匹配）自动提供。跟踪存在几个主要问题：

  • 遮挡
  • 多目标跟踪
  • 尺度、光照和外观变化
  • 困难和快速运动
  • ...

尽管对象跟踪问题已经存在多年，但尽管有许多对象跟踪器，即使是为特殊目的构建的，以及那些试图普遍解决问题的跟踪器，它仍然没有得到解决。

卡尔曼滤波器，尽管它们可以用于许多其他目的，但经常用于对象跟踪。它们特别适用于已知运动模型的对象，此外，它们还结合了一些额外信息，以便更鲁棒地估计下一个对象位置。它们可以在某些约束条件下用于通用单目标跟踪。本文将解释卡尔曼滤波器背后的主要思想，并将重点介绍其在对象跟踪中的实际应用以及示例。

卡尔曼滤波器 - 主要思想

假设我们有某种检测器，并且我们的检测器不完善：它容易产生误报，并不总是能检测到对象，检测不完善（不提供精确的位置和尺度），而且执行成本高昂。我们还假设我们正在跟踪一名足球运动员。检测到对象后，我们希望利用关于对象的信息，尽可能鲁棒地跟踪它。我们的检测器只会给我们对象的位置，所以我们必须尽可能地利用它。为了预测玩家的下一个位置，我们将需要一个对象运动模型（例如，匀速运动、匀加速运动）。我们的检测器不完善，所以对象位置存在噪声，通常称为测量噪声。此外，选定的运动模型不会完美地描述玩家的运动，所以我们也存在与模型相关的噪声，称为过程噪声。我们希望仅通过以下三个参数来估计玩家的下一个位置：

  1. 对象运动模型
  2. 测量噪声
  3. 过程噪声

因此，我们可以有效地重新检测它，并有望应对对象遮挡。接下来的章节将向您展示如何做到这一点。

Kalman filter cycle.
卡尔曼滤波器的循环。 卡尔曼滤波器的大部分工作可以归结为传播和更新高斯分布，并更新其协方差。首先，滤波器根据提供的状态转换（例如运动模型）预测下一个状态，然后，如果适用，将有噪声的测量信息纳入校正阶段。这个循环会重复进行。

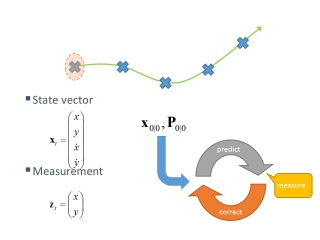
初始状态

我们将首先介绍初始状态以及我们试图实现的目标。以下图片展示了初始状态并同时介绍了最相关的术语。

概述： 仅使用估计和当前状态，我们希望预测下一个状态。第二步（校正）包括有噪声的测量，以便应用状态更新。 初始状态类型： 顶部的绿线表示我们要跟踪的对象，蓝色 X 标记了对象的真实位置。我们希望使用恒定速度模型来模拟运动。因此，状态将包括对象在两个方向上的位置和速度。检测器给我们的是有噪声的对象位置，因此位置是我们的测量值。
初始状态值： 为了开始跟踪过程，我们需要知道初始状态 x0|0 的值。我们还需要有初始不确定性，这由高斯协方差矩阵 P0|0 表示。顶部的橙色椭圆表示描述位置不确定性的二维高斯分布。初始矩阵 P0|0 通常是对角矩阵（假设分量不相关），其中每个分量都有其自己的不确定性 L - 高斯西格玛。

阅读本节时请记住

  • x(t) - 状态向量
  • z(t) - 测量
  • P(t|t-1) - 过程协方差矩阵

预测

预测是第一步，包括下一个状态（位置和速度）预测以及更新我们对对象状态的不确定性（增加不确定性）。

1a) 状态预测： 第一步是使用运动模型预测下一个状态。下一个状态 x(t|t-1) 是通过将前一个状态乘以状态转移矩阵 - F 得到的。Q 表示过程噪声，由于我们处理的是高斯分布，因此它必须服从正态分布。 1b) 协方差预测： 协方差更新是通过将前一次迭代的协方差矩阵乘以状态转移矩阵 F（运动模型）并加上可以为常数的加性过程噪声 Q 完成的。我们预测的更新协方差更宽，因为我们对估计的确定性降低了。
* 状态转移矩阵： 运动模型必须用矩阵 F 表示，因此它必须是线性的。如果模型不是线性的，则必须在某个工作点进行线性化，这在扩展卡尔曼滤波器中使用。所使用的模型是恒定二维速度运动模型，其中位置更新为：p(t) = p(t-1) + v * p(t-1)，其中 p 表示位置，v 表示速度；速度保持恒定。速度被标记为位置随时间的变化率。如果我们多次执行预测步骤，估计位置将遵循恒定速度模型（蓝色点）。协方差矩阵每次都会变宽（蓝色椭圆），因为我们对对象位置的不确定性增加了。

阅读本节时，请记住

  • F - 状态转移矩阵
  • Q(t) - 过程噪声协方差

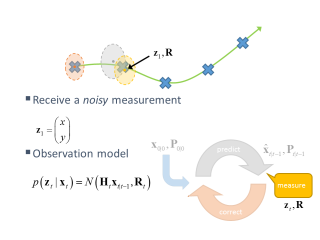
正确

获得有噪声的测量后，校正步骤开始。它包含卡尔曼滤波器更新，包括状态更新和不确定性更新（减少不确定性）。

* 测量： 当（如果）我们收到有噪声的测量（在我们的案例中，是从检测器获得的位置）时，更新过程开始。有噪声的测量 z(t) 被建模为单个高斯分布，其中噪声被建模为通常是常数的协方差矩阵 R(t)。测量的不确定性以金色椭圆表示。 2a) 测量更新： 为了计算校正所需的预测测量值，我们必须从状态中选择测量分量。测量值与状态具有相同的结构，或者它只包含状态的一部分；在我们的例子中，只是对象位置。矩阵 H 是模型选择矩阵，当它与状态相乘时，只选择属于测量值的元素。
* 残差： 为了进行校正，我们必须知道预测误差。因此，计算残差，也称为创新，用 y(t) 表示。残差是通过预测测量值和获得的测量值之间的差异来计算的——参见绿色和金色椭圆。残差协方差 S 以类似的方式计算。 * 卡尔曼增益： 卡尔曼增益 K 指定了我们对预测的信任程度与我们对测量的信任程度。它是预测过程协方差矩阵 P、观测模型 H 和逆残差协方差 S 的乘积。让我们研究两种极端情况：
  • 我们对测量值有信心（我们相信我们的检测器）
    在这种情况下，测量噪声矩阵 R 非常小，导致 K 减小，测量值比预测值权重更大。
  • 我们对预测有信心（我们相信我们的运动模型，而不是很相信检测器）
    在这种情况下，测量噪声矩阵 R 非常大，导致 K 增加，测量值比预测值权重小得多。
2b) 校正： 卡尔曼增益现在用于更新状态 x 和协方差矩阵 P，如图所示。结果是更新后的位置，用金色椭圆表示。 * 最后一步 校正步骤完成后，下一步，再次是预测步骤。这两个步骤迭代运行，以跟踪对象，如图所示。

阅读本节时，您应该知道什么是

  • R(t) - 测量噪声

现在，当您了解了基础知识后，是时候进行实际示例了，但首先简要介绍一下实现。

实现

所提供的实现是通用的：DiscreteKalmanFilter<TState, TMeasurement>。通用参数是状态类型（TState）和测量类型（TMeasurement）。这种实现方式增加了一个抽象层，从而实现了

  • 更容易的代码处理
  • 更容易的调试
  • 可扩展性

下面的类图显示了实现的概述

Class diagram.
类图。 卡尔曼滤波器的实现包括两个类——一个抽象类和一个实现离散卡尔曼滤波器的具体类。常见的运动模型也已实现。

假设我们要使用恒定速度模型，并且测量模型是对象的位置（正如上图所示）。此示例的用法示例如下所示。

初始化

最复杂的步骤是初始化。我们必须设置：过程噪声和测量噪声（Q 和 R）、过程协方差矩阵（P）、状态转移矩阵（F）和模型选择矩阵（H）。内置模型极大地简化了此任务。由于灵活性，初始化步骤稍长。例如，扩展卡尔曼滤波器需要每个步骤都改变的转移矩阵。此外，过程噪声和测量噪声（Q 和 R）可能不是常数，因此它们也可以在每个步骤中改变。

using ModelState = Accord.Extensions.Statistics.Filters.ConstantVelocity2DModel;
KalmanFilter<ModelState, PointF> kalman = null;

var measurementDimension = 2; //just coordinates
var initialState = new ModelState { Position = new PointF(0,0), Velocity = new PointF(0.5f, -2f)};
var initialStateError = ModelState.GetProcessNoise(accelerationNoise: 10); //process cov. mat. - P(0|0)

//create Kalman filter
kalman = new DiscreteKalmanFilter<ModelState, PointF>(   
                initialState, initialStateError,  //x(0) and P(0|0)
                measurementDimension /*(position)*/, 0 /*no control*/,
                //state and measurement <=> array conversion
                x => ModelState.ToArray(x), x => ModelState.FromArray(x), x => new double[] { x.X, x.Y }); 
                
kalman.ProcessNoise = ModelState.GetProcessNoise(accelerationNoise: 10.0); //process noise - Q
kalman.MeasurementNoise = Matrix.Diagonal<double>(kalman.MeasurementVectorDimension, 1.3); //measurement noise - R
           
kalman.MeasurementMatrix = ModelState.GetPositionMeasurementMatrix(); //measurement selection mat. - H
kalman.TransitionMatrix = ModelState.GetTransitionMatrix(); //state transition matrix - F

预测

预测步骤只包含一个方法，如果没有任何测量，该方法将重复执行，而不进行校正。

kalman.Predict(); //predict next state

正确

校正方法接收有噪声的测量值（例如从检测器获得）。

PointF objectPosition = .... //the position obtained by detector
kalman.Correct(objeectPosition); //correct predicted state by measurement
Console.WriteLine(kalman.State.Position.X + " " + kalman.State.Position.Y);

结论

本文介绍了用于目标跟踪问题的离散卡尔曼滤波器及其在 C# 中的实现。如果运动模型是线性的，并且过程噪声和测量噪声是类高斯分布的，那么卡尔曼滤波器代表了状态更新（在我们的案例中是跟踪问题）的最佳解决方案。这些条件在绝大多数应用中都得到了满足。

源代码和示例代码是 Accord.NET Extensions Framework 的一部分，该框架提供了许多主要用于图像处理、对象检测和跟踪的高级算法，所有这些都打包为流畅的扩展和简单直观的泛型，所以不要忘记看一看 :)

参考文献

[1] Smith K. "计算机视觉精选主题 - 2D 跟踪 1/2 IJACI"
迄今为止最好的对象跟踪教程 - 本文中使用了一些幻灯片
[2] Kantor G. "卡尔曼的美丽滤波器"
[3] Kalman, R. E. (1960). "线性滤波和预测问题的新方法"。Journal of Basic Engineering 82 (1): 35–45

历史

  • 2015年1月16日 - 发布第一版
© . All rights reserved.