在 Matlab 中实现梯度下降来解决线性回归问题

• 下载 Linear_Regression_With_One_Variable.zip - 1.9 KB
• 下载 Linear_Regression_With_Multiple_Variables.zip - 1.5 KB

引言

本文围绕 Andrew Ng 在 Coursera 上的机器学习课程展开，我强烈推荐你去看看，它内容非常丰富。在本文中，我将更侧重于第一部分（单变量线性回归¹）的编程部分。

人工智能是当今计算机科学中最有趣的领域之一，而其最有用的领域之一就是机器学习。

机器学习无疑是当今技术中应用最广泛的人工智能形式之一，它用于语音识别、手写识别、垃圾邮件分离、在搜索引擎上搜索时显示最相关的网站以及许多其他方面。

你需要知道的事情

了解矩阵和向量是必要的，因为代码中会用到矩阵乘法，但如果你不熟悉这个概念，不用担心。我将尽可能详细地解释每个步骤。

但是，了解一些 Matlab 并熟悉编码概念对于充分利用本文是必要的。

概念

现在我可以直接告诉你线性回归的理论定义，但因为这是一个动手教程，我宁愿通过一个例子来解释它。

所以假设我们收集了社区的房价数据，这些数据包含每栋房屋的平方米大小和相应的价格，我们想编写一个简单的软件，利用这些数据进行训练，以预测房屋基于其大小的价格²。

解决这个问题的方法之一是线性回归，它基本上是一种寻找问题因变量（在本例中为：价格）和问题自变量（在本例中为：大小）之间关系的方法。现在在这个问题中，我们只有一个自变量，换句话说，我们只处理房屋的一个特征（即房屋的大小），在这种情况下，我们将使用一种称为简单线性回归或单变量线性回归的线性回归形式。

线性回归

学习线性回归如何工作的最好方法是使用一个例子
首先让我们可视化我们的数据集

现在我们要做的是找到一条最能拟合这些数据的直线³，这条线将是我们的假设，我们这样定义它的函数：

• θ₁ 是我们直线的截距
• θ₂ 是我们直线的斜率
• x 是房屋的大小
• h(x) 是给定大小的房屋的预测价格

现在为了让我们的假设尽可能接近真实值，我们必须得到正确的截距和斜率，我们可以通过最小化我们的成本函数来做到这一点。那么什么是成本函数呢？

成本函数

我们的成本函数（或平方误差函数）可以这样定义

• θ 是一个二维向量，包含我们的 θ₁ 和 θ₂
• m 是我们训练样本的数量
• x_i 是我们数据集中第 i 个训练样本的大小
• y_i 是我们数据集中第 i 个训练样本的价格

现在让我来解释一下这个函数是什么，首先，我们看到开头的 ( 1/2m )，这只是为了让推导过程更容易一些⁴，所以不用担心。

接下来，我们看到 ( h_θ(x_i) - y_i )，如果你还记得，h(x) 是给定大小 (x) 的预测价格，而这部分函数只是计算第 i 个训练样本的真实价格与第 i 个训练样本的预测价格（相对于 θ）之间的差异，所以它实际上是计算预测的误差，我们将这个值平方的原因是为了消除这个误差前面的符号，因为它可以是正的也可以是负的，最后求和是为了将我们训练集中所有样本的误差相加。

所以成本函数实际上是计算我们的预测偏差了多少，因此解决这个问题的关键是最小化我们的成本函数，换句话说，使其尽可能小，为了做到这一点，我们必须为我们的 θ₁ 和 θ2 选择正确的值。

事实证明，做到这一点的方法之一是使用一种称为梯度下降的算法。

梯度下降

为了向你解释梯度下降是什么以及它是如何工作的，绘制我们的成本函数会有所帮助，所以我们的成本函数可能会看起来像那条蓝线

现在那个红色圆圈是你可能根据你的数据集和初始 theta（包含截距和斜率的二维向量）而结束的地方，那个绿色圆圈是你想要结束的地方，因为如果你还记得，我们的成本函数的工作是计算我们的预测偏差了多少，所以这个函数的最小值意味着获得最准确的预测。但问题仍然存在，我们如何到达那个绿色圆圈？

事实证明，有一种有用的算法叫做梯度下降，这个算法基本上会朝着函数的局部最小值迈出多个步骤，并在找到它时收敛。

那么首先让我们看看梯度下降是什么样子的

现在让我们解释一下它是如何工作的，这个公式似乎是通过某个值来减小 θj，这个值是我们的成本函数对 theta（相对于 θj）的偏导数乘以 alpha（即所谓的学习率），然后将结果赋值给 θj。但这非常令人困惑和复杂，所以我会单独解释这个公式的每个元素。

首先，你应该知道，当我提到参数时，我指的是我们的 theta 向量，它是一个二维向量，包含我们假设直线的截距和斜率。

现在让我们从我们的成本函数对 theta 的偏导数（相对于 θj）开始，这个偏导数实际上是与我们的成本函数对 theta 相切的直线的斜率，它看起来像这样

上图中，红色圆圈是特定 theta 向量的成本函数值，粗蓝色线是该圆圈的切线，该线的斜率是特定 theta 向量的成本函数的偏导数。现在，这个算法的聪明之处在于它利用切线斜率的符号来决定增加还是减少我们的参数（截距和斜率）的值，并且利用切线斜率的值来决定改变这些值的多少，这使得它对最小化函数很有用。

通过上述解释，现在很清楚这个算法是如何工作的。它简单地取我们的每个参数 θj（我们 theta 向量中的第 j 项），并根据我上面解释的切线斜率增加/减少它。如果你重复这个过程足够多的次数，它会修改我们的参数，以便当我们将其代入成本函数时，我们得到一个尽可能接近零的结果，而那个 alpha 只是一个称为学习率的数字，我们选择它来决定我们的梯度下降步长有多大（我们将在编程部分更多地讨论它）。

所以我几乎解释了解决我们问题所需知道的一切，在下一节中，我们将在 Matlab 中实现这个算法并解决问题。

实现梯度下降

我认为最好是逐个文件地讲解代码，所以首先我将解释每个文件的作用，以便你了解程序的运行方式。

main.m 是准备我们算法所需的所有数据的文件，将这些数据传递给另一个实际包含算法实现的函数，然后向我们展示结果。

gradient.m 是包含梯度函数和梯度下降实现的文件。

cost.m 是一个简短而简单的文件，其中包含一个根据其参数计算成本函数值的函数。

main.m

所以首先，我们加载将用于训练我们软件的数据集。

% Loading the dataset

dataSet = load('DataSet.txt');

% Storing the values in seperate matrices

x = dataSet(:, 1);

y = dataSet(:, 2);

这段代码块基本上是将存储在 DataSet.txt 中的逗号分隔数据列表加载到一个名为 dataSet 的变量中。dataSet 是一个有 2 列的矩阵，第一列是大小，第二列是价格。我们将第一列填充到变量 x 中，将第二列填充到变量 y 中。

% Do you want feature normalization?

normalization = true;

% Applying mean normalization to our dataset

if (normalization)

    maxX = max(x);
    minX = min(x);
    x = (x - maxX) / (maxX - minX);

end

在这一部分，我们正在进行一项称为特征归一化的操作。这是一种在机器学习中经常使用的技巧，事实证明它通过归一化数据确实有助于梯度下降达到收敛，那么这意味着什么呢？

你看，通常在机器学习中，我们的数据集包含非常大的数字，这在许多情况下会导致很多问题，更糟糕的是，当你的数据集中有一组特征在 1 到 5 的范围内，而另一组特征在 1000 到 200000 的范围内时，这可能会导致很多问题，那么我们该怎么办呢？

处理此类问题的一种方法是使用一种称为均值归一化的方法。要应用均值归一化，您只需将以下公式应用于数据集中的每个样本

• x_i 是第 i 个训练样本
• max(x) 是我们数据集中的最大值
• min(x) 是我们数据集中的最小值

现在我们要做的是将这个公式应用于我们数据集中每一个值。当我这样说时，程序员首先想到的可能是一种循环，你可以使用任何类型的循环来完成，但 Matlab 原生支持向量和矩阵，所以我们可以使用它们来编写更简洁、更高效的代码（这就是我在上面的代码中做的）。现在让我解释一下这段代码是如何工作的⁵。

所以代码是

x = (x - maxX) / (maxX - minX);

上面代码中的变量 x 是一个 nx1 矩阵，包含我们所有房屋大小，而 max() 函数简单地找到该矩阵中的最大值，当我们从矩阵中减去一个数字时，结果是另一个矩阵，该矩阵中的值看起来像这样

然后我们将这个矩阵除以另一个数，这个数是我们原始向量 max(x) 中的最大值减去原始向量 min(x) 中的最小值。矩阵除以一个数的过程与它们相减的过程完全相同，只是我们用除法代替减法，将每个条目除以这个数。我过去犯的一个错误是归一化 y 矩阵，你不应该归一化因变量，除非在特殊情况下并且你真正知道自己在做什么。

你可能想知道为什么我在使用 min 和 max 之前将它们存储在变量中，那是因为稍后我们将不得不归一化输入值以获得正确的预测。

所以现在我们有一个名为 x 的变量，其中包含我们数据集的归一化值，以及一个名为 y 的变量，其中包含我们房屋的价格。

% Adding a column of ones to the beginning of the 'x' matrix

x = [ones(length(x), 1) x];

% Plotting the dataset

figure;

plot(x(:, 2), y, 'rx', 'MarkerSize', 10);

xlabel('Size ( squared meters )');

ylabel('Price');

title('Housing Prices'); 

** 如果你不熟悉 plot 函数，不用担心，它不是必需的，仅用于展示我们的工作和调试 **

这段代码的第一部分只是在我们的 x 矩阵中添加一列 1，x 现在是一个 nx2 矩阵，第一列是 1，稍后我将解释为什么我这样做。

在第二部分，我们只是绘制我们的数据集，看看我们正在处理什么（本质上是一个调试代码）。

% Running gradient descent on the data

% 'x' is our input matrix

% 'y' is our output matrix

% 'parameters' is a matrix containing our initial theta and slope

parameters = [0; 0];

learningRate = 0.1;

repetition = 1500;

[parameters, costHistory] = gradient(x, y, parameters, learningRate, repetition);

现在这就是一切发生的地方，我们正在调用一个名为 gradient 的函数，它根据我们发送的参数对我们的数据运行梯度下降，它返回两个东西：第一个是 parameters ，它是一个矩阵，包含最适合我们数据集的直线的截距和斜率；第二个是另一个矩阵，包含梯度下降每次迭代的成本函数值，以便稍后绘制成本函数（另一个调试步骤）。

好的，让我们解释一下参数，x 是一个 nx2 矩阵，包含一列 1 和另一列归一化的房屋大小，y 是一个 nx1 矩阵 ，包含归一化的房屋价格，parameters 是一个 2x1 矩阵，包含我们假设线的初始截距和斜率值，learningRate 是我们梯度下降算法中的 alpha，repetition 是我们将对数据运行梯度下降的次数。

没有确定的方法来确定最佳学习率和重复次数值，你只需反复尝试才能为你的数据集找到最佳值，尽管绘制成本函数可以帮助你，因为它让你看到算法完成任务的好坏。

% Plotting our final hypothesis

figure;

plot(min(x(:, 2)):max(x(:, 2)), parameters(1) + parameters(2) * (min(x(:, 2)):max(x(:, 2))));

hold on;

** 此时，假设线的截距和斜率已被算法修改，得到的线最能拟合我们的数据。 **

这部分只是绘制我们的假设线，乍一看可能很复杂，但它不言自明，我将解释这些函数的作用，你只需通读即可理解，这也是另一个调试步骤。

• parameters(1) 是我们假设线的截距或 θ₁
• parameters(2) 是我们假设线的斜率或 θ₂

% Plotting the dataset on the same figure

plot(x(:, 2), y, 'rx', 'MarkerSize', 10);

这部分只是在绘制假设线的同一个窗口中绘制我们的数据集。

% Plotting our cost function on a different figure to see how we did

figure;

plot(costHistory, 1:repetition);

这只是在另一个窗口中绘制我们的成本函数，以查看我们做得如何（用于调试目的）。

% Finally predicting the output of the provided input

input = 120;

if (normalization)
    input = (input - maxX) / (maxX - minX);
end

output = parameters(1) + parameters(2) * input;

disp(output);

最后，我们预测了一个特定大小（120）的价格并显示结果。当然，这只是一个虚拟数据集，训练样本的数量太少，无法做出准确的预测。请注意，如果你归一化了特征，则必须归一化此输入变量才能获得正确的预测。

gradient.m

这是实际对数据运行梯度下降并调整假设线参数以使其最适合我们训练集的函数。

所以首先，我们将这样声明这个函数

function [ parameters, costHistory ] = gradient( x, y, parameters, learningRate, repetition )

在上面的代码中，我们只是声明了一个名为 gradient 的函数，它接受五个参数并返回两个值。我之前已经解释过这些，但我们现在快速回顾一下

parameters 是此函数返回的第一个值，它是一个 2x1 矩阵，包含我们假设线的截距和斜率。请注意，我们的参数中还有另一个名为 parameters 的变量，它与此变量本质上相同，只有一个区别，函数参数中的那个尚未被算法修改，因此它包含初始截距和斜率，在本例中为零，函数返回的变量是同一个变量，但现在它已被算法修改，并包含可能最适合我们数据的线的截距和斜率。

costHistory 是我们的函数返回的第二个值，它是一个 nx1 矩阵，它将包含梯度下降每次迭代的成本函数值，这在我们稍后尝试为特定数据集找到最佳学习率，或者我们只是想找出我们的算法是否正确工作时会派上用场。

x 是一个 nx2 矩阵，包含一列 1 和另一列我们的自变量，在这种情况下是我们的房屋大小。

y 是一个 nx1 矩阵，包含我们的因变量，在这种情况下是我们的房屋价格。

learningRate 和 repetition 是不言自明的，我还在上一节中解释过它们。

% Getting the length of our dataset

m = length(y);

% Creating a matrix of zeros for storing our cost function history

costHistory = zeros(repetition, 1); 

在上面的代码中，我们将训练样本的数量存储在一个名为 m 的变量中，我们还预先分配了一个名为 costHistory 的 nx1 矩阵，我之前解释过。请注意，我们正在使用 repetition 变量来确定将存储在此向量中的值的数量，原因是在梯度下降的每次迭代中，我们的假设线的截距和斜率都会有不同的值，因此在每次迭代中，我们的成本函数都会有不同的值。

% Running gradient descent

for i = 1:repetition        

    % Calculating the transpose of our hypothesis

    h = (x * parameters - y)';        

    % Updating the parameters

    parameters(1) = parameters(1) - learningRate * (1/m) * h * x(:, 1);

    parameters(2) = parameters(2) - learningRate * (1/m) * h * x(:, 2);        

    % Keeping track of the cost function

    costHistory(i) = cost(x, y, parameters);        

end 

现在我们来到代码的主要部分，即实现梯度下降。首先，我们将创建一个 for 循环，我认为这是不言自明的。

在 for 循环内部是所有事情发生的地方，首先让我解释一下我们正在使用的公式，所以我们说过梯度下降的公式是这样的

如果我们代入成本函数的定义并考虑我们有两个参数（截距 和 斜率），我们最终会得到这样一个算法

现在让我们计算这些偏导数以使实现更容易

有很多方法可以实现这一点，我建议使用你最理解的方法，但我将使用的方法可能是最短和最有效的，所以让我们逐行解释它，首先我们从这一行开始

h = (x * parameters - y)';

这行代码的全部目的是计算我们两个公式中的那个求和，解释这个最好的方法是使用图片，所以首先我将向你展示 x * parameters 会是什么样子

** 如果你不知道如何进行矩阵乘法，只需快速搜索一下，这非常简单 **

因此，在将这些矩阵相乘之后，我们得到另一个矩阵，其中包含我们训练集中每个大小的预测价格或 h(x)，顺便说一下，这就是我在 main.m 中将该列 1 添加到此矩阵的原因。现在我们必须从这些价格中减去真实价格或 y

现在我们几乎将算法的整个求和部分放入一个矩阵中，但是为了继续进行并完成其余的计算，我们必须转置这个矩阵，在这种情况下，这基本上意味着将其转换为一个向量，你稍后会明白我为什么这样做

现在这个向量保存在一个名为 h 的变量中，我们已经准备好进入代码的下一部分

parameters(1) = parameters(1) - learningRate * (1/m) * h * x(:, 1);
parameters(2) = parameters(2) - learningRate * (1/m) * h * x(:, 2);

• parameters(1) 是 θ₁
• parameters(2) 是 θ₂

这部分实际上非常容易理解，但我还是要说明整个过程。现在如果你看梯度下降的原始公式，你会注意到修改 θ₁ （截距）和 θ₂ （斜率）之间有细微的差别，在修改 θ₂ 的最后还有另一个乘法，它是求和的一部分，所以对于 θ₂，我们基本上需要将变量 h 中的每个对象乘以其对应的大小或 x_i，我们再次使用矩阵乘法来做到这一点。但如果你阅读代码，你会发现我们在两行中都乘以 x，但第一行只乘以 x 矩阵的第一列，它本身就是由 1 组成的另一个矩阵，所以这个乘法不会对 h 向量中的值产生任何影响，但如果你进行乘法，你会发现它实际上是将 h 向量中的所有条目相加，并给我们一个标量值（一个数字）来处理，这正是我们想要的。这也是我们转置变量 h 的原因。

然而，在代码的第二行中，我们正在将修改后的斜率（θ₂）乘以 x 矩阵的第二列，该列包含我们数据集中房屋的大小，这正是根据梯度下降的原始公式我们想要的。该乘法将看起来像这样

结果将是一个标量值（一个数字），如果你用 h(x_i) 替换 θ₁ + x_i θ₂ ，即我们的假设函数，你会发现这个结果与梯度下降中修改 θ₂ 的原始公式末尾的求和完全相同。

现在我们有了两个求和，其余的就很容易了，我们只是将求和乘以 1/m 和我们的 learningRate ，然后从它们对应的 theta 中减去它们。

好的，现在我们已经修改了假设线的截距和斜率一次，我们离成本函数的局部最小值更近了一点，是时候编写必要的代码来跟踪成本函数，以便进行调试和选择正确的 learningRate 和 repetition 值，方法是计算我们最近修改的参数的成本函数的返回值，并将它们保存到我们之前创建的预分配向量的一个槽中

costHistory(i) = cost(x, y, parameters);

这一行是不言自明的，成本函数本身的代码在下一节中解释。

cost.m

function [ cost ] = cost( x, y, parameters )

    %   Calculates the cost function

    cost = (x * parameters - y)' * (x * parameters - y) / (2 * length(y));    

end

这部分的代码非常简短直接，所以我们开始吧。

第一行定义了一个函数，它返回一个名为 cost 的变量，它显然将包含特定数据集和一组参数（截距和斜率）的成本函数值，它需要三个参数，包括

• x：一个 n*2 矩阵，由一列 1 和另一列包含房屋大小组成
• y：一个 n*1 矩阵，包含我们所有房屋的价格
• parameters：一个 2*1 矩阵，包含 θ₁ 或 截距和 θ₂ 或我们假设线的斜率

现在让我们再次看看成本函数，只是为了提醒自己它长什么样

好的，现在让我们解释一下代码，代码由三部分组成

1. (x * parameters - y)'
2. (x * parameters - y)
3. (2 * length(y))

第一部分和第二部分的计算已在上一节中详细解释，这里我们只看看它们的样子以及它们的乘积是什么。

第一部分看起来像这样

第二部分看起来像这样

它们的乘积结果将看起来像这样

这（再次）是一个标量值（一个数字），如果你用 h(x_i) 替换 θ₁ + x_i θ₂ ，即我们的假设函数，你会发现它与原始成本函数中的那个求和完全相同。

我们最后将整个结果除以代码的第三部分，即 2*length(y) ，或我们 y 矩阵中值的两倍，现在我们得到了这些特定参数的成本函数值。

测试看它是否有效！

好的，现在我们来实际测试这个程序，看看它运行得如何。首先我将使用另一个虚拟数据集，其中包含一些更容易预测的值，只是为了确保一切正常运行，然后我们再转到房价数据集。

TestDataSet.txt 包含在文章的 rar 文件中，它看起来像这样

1,2

2,4

2,5

3,6

3,7

4,8

5,10

6,12

6,13

6,13

8,16

10,19

所以每个“y”几乎都是“x*2”，现在我们要把这些数据输入到我们的程序中。

这个数据集实际上不需要归一化，但我们将尝试归一化和不归一化两种方法，以确保它们都有效。

你需要注意的一点是，你需要为“learningRate”和“repetition”设置不同的值，这与你的数据集以及你是否正在归一化你的特征有关。你可以通过实验并查看成本函数的图表来找到这些变量的合适值，例如，如果你使用大值，你的 theta 将得到 Inf（无穷大），因此程序将失败。

在对该数据集进行实验后，我发现以下值在不进行归一化的情况下运行良好

learningRate = 0.01;

repetition = 1500;

归一化后可以使用这些值

learningRate = 1;

repetition = 100;

现在看看重复值之间的巨大差异，你会发现通过归一化，程序只需十五分之一的重复次数就能收敛，这使得程序收敛得更快。

好的，这些是没有使用特征归一化的结果

这是我们数据集的图表

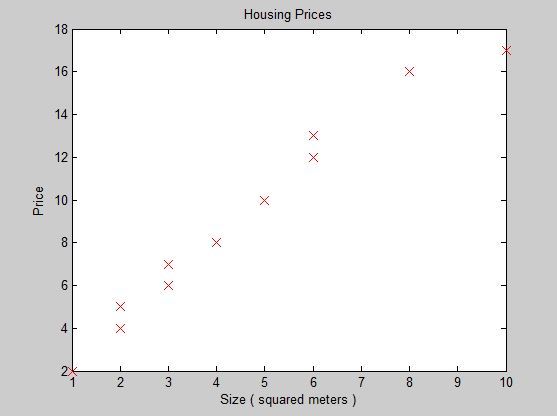
这是我们的程序得出的假设线

现在你可以看到它得出了一个很好的假设线，它覆盖了我们大部分样本，并且很可能给我们准确的预测。

这是成本函数的图

请注意它是如何从顶部开始并以几乎为零结束的。

现在我们要开始进行归一化

这是程序为我们归一化特征得出的假设线

如你所见，尽管算法运行了100次而不是1500次，我们几乎得到了相同的假设线。

这是特征归一化后的成本函数图

此图清晰地展示了程序将成本函数最小化到接近零的良好效果。

无论是否进行归一化，程序都给出了输入为 5 时预测值约为 10，这正是我们期望得到的。

现在对于房价数据集，我强烈建议使用特征归一化，我能够在没有归一化的情况下使成本几乎为零，但学习率 (≈0.0000001) 和重复次数 (≈50000) 效率非常低，但使用归一化后，当学习率设置为 1.3，重复次数设置为 500 时，它会收敛。

这是数据在图表上的样子

现在因为这个数据集中的数据非常分散，线性回归可能不是一个好主意，我们不会得到准确的结果，但我们仍然会尝试

这是我们的程序得出的假设线，它看起来会给我们一些平均预测，但为了了解程序做得有多好，以及是否能做得更好，我们必须查看成本函数图。

现在你可以看到在算法结束时成本几乎为零，所以上面的线在线性回归中已经达到最佳状态，我输入了一些数据集中存在的输入，在大多数情况下，它对真实价格的预测误差约为 ±30，考虑到数据集不太适合线性回归，这已经相当不错了。

结论

这就是你需要在 Matlab 中实现梯度下降以解决线性回归问题所需的所有信息。

请记住，在这个例子中，我们使用的是单变量线性回归，并且数据集非常有限，因此结果不会非常准确，但如果你应用这些技术并使用更好的数据集，你将得到非常令人满意的结果。

此外，我还实现了梯度下降来解决 Matlab 中的多元线性回归问题，链接在附件中，它与单变量非常相似，所以如果你想，可以去看看，这实际上是我在这个网站上的第一篇文章，如果我得到好的反馈，我可能会发布关于多元代码或其他人工智能方面的文章。

希望本文内容对您有所帮助，如果您有任何问题或建议，请留言。

参考文献

1. 本文中使用的线性回归问题和数据集也来自 Coursera。
2. 房屋可能存在也可能不存在于我们的训练集中。
3. 这条线不一定是直的，但因为直线是最简单的情况，我们将使用它。
4. 我们需要得到这个函数对于我们主要算法的偏导数。
5. 该代码的第一部分只是为了能够更轻松地在归一化和不归一化之间切换，你可以忽略它。