使用二叉树进行快速 LZW 压缩
4.78/5 (61投票s)
使用二叉树作为字典的快速 LZW 实现
引言
有一天,我和一位同事谈论压缩时,令我惊讶的是,他告诉我有一种算法在压缩时使用字典,然后将其放在一边,并保存压缩后的数据而无需字典。我问他:“它如何重新构建原始数据?”,他回答:“只需在解压缩过程中重新构建字典即可!!!”
这就是 LZW 压缩。我那天决定阅读有关它的信息并尝试实现这个非常好的想法算法,我花了很长时间来尽可能快地实现它,但我认为我失败了,因为它在正常情况下每秒压缩 1MB。代码似乎很难理解,但如果您通过背景部分或页面下方的任何参考来查看算法,就会很容易理解。
背景
1984 年,Terry Welch 正在为高性能磁盘控制器开发一种压缩算法。他开发了一种相当简单的算法,该算法基于 LZ78 算法,现在称为 LZW。LZW 是一种无损的“基于字典”的压缩算法。基于字典的算法扫描文件以查找出现次数多于一次的数据序列。然后将这些序列存储在字典中,并在压缩文件中,在重复数据出现的地方放置引用。
LZW 思想
LZW 压缩用单个代码替换字符序列。它不分析传入的文本。相反,它只是将它看到的每个新字符序列添加到字符串表中。当输出单个代码而不是一串字符时,就会发生压缩。因此,字典中的任何代码都必须只在压缩缓冲区中第一次出现一个字符串。这意味着字典只是引用压缩缓冲区中的未压缩字符串,而无需让字典复制这些字符串。因此,不必保留字典来解码 LZW 数据流。这可以节省大量存储 LZW 编码数据空间。
LZW 算法输出的代码可以是任意长度的,但它必须比单个字符具有更多的位数。默认情况下,前 256 个代码(使用 8 位字符时)分配给标准字符集。其余代码在算法进行时分配给字符串。示例程序运行时的代码长度为 12 位到 31 位。这意味着,代码 0-255 指的是单个字节,而代码 256-2^n 指的是子字符串,其中 n 等于每个代码的位数,如下面的图所示。

LZW 算法
压缩
LZW 压缩算法可总结如下
w = NIL;
while ( read a character k )
{
if wk exists in the dictionary
w = wk;
else
{
add wk to the dictionary;
output the code for w;
w = k;
}
}
原始算法使用 4094 个条目的字典;前 256 个用于 ASCII 代码,其余用于子字符串。如您所见,算法一次扫描一个字符。如果字符串在字典中,则将字符添加到当前字符串并处理下一个字符。如果工作字符串不在字典中,则将工作字符串添加到字典中,然后发送不带新字符的工作字符串。然后将工作字符串设置为新字符。
压缩示例
Input string is "^WED^WE^WEE^WEB^WET".
w k output index symbol
-----------------------------------------
NIL ^
^ W ^ 256 ^W
W E W 257 WE
E D E 258 ED
D ^ D 259 D^
^ W
^W E 256 260 ^WE
E ^ E 261 E^
^ W
^W E
^WE E 260 262 ^WEE
E ^
E^ W 261 263 E^W
W E
WE B 257 264 WEB
B ^ B 265 B^
^ W
^W E
^WE T 260 266 ^WET
T EOF T
[1] 通过算法的开头进行此字符串的逐步操作,您可以看到在循环的第一次通过中,会检查字符串 “^W” 是否在表中。由于不在,因此输出 “^” 的代码,并将字符串 “^W” 添加到表中。由于我们已经为代码 0-255 定义了 256 个字符,因此第一个字符串定义可以分配给代码 256。在读取第三个字母“E”之后,第二个字符串代码“WE”被添加到表中,并输出字母“W”的代码。这个过程一直持续到第二个单词,读取字符“^”和“W”,匹配字符串编号 256。在这种情况下,输出代码 256,并将一个三字符字符串添加到字符串表中。该过程继续进行,直到字符串耗尽并且所有代码都已输出。
解压缩
LZW 解压缩算法如下
read a character k;
output k;
w = k;
while ( read a character k )
// k could be a character or a code.
{
entry = dictionary entry for k;
output entry;
add w + entry[0] to dictionary;
w = entry;
}
如前所述,解压缩会构建自己的字典,该字典与压缩器的字典完全匹配,因此只需保存代码即可进行压缩。
解压缩示例
Input string is "^WED<256>E<260><261><257>B<260>T".
w k output index symbol
-------------------------------------------
^ ^
^ W W 256 ^W
W E E 257 WE
E D D 258 ED
D <256> ^W 259 D^
<256> E E 260 ^WE
E <260> ^WE 261 E^
<260> <261> E^ 262 ^WEE
<261> <257> WE 263 E^W
<257> B B 264 WEB
B <260> ^WE 265 B^
<260> T T 266 ^WET
[1] 与压缩算法一样,它每次读取新代码时都会将一个新字符串添加到字符串表中。除了这些之外,它所需要做的就是将每个传入的代码翻译成字符串并发送到输出。需要注意的重要一点是,最终的字符串表看起来与压缩过程中构建的表完全相同。输出字符串与压缩算法的输入字符串相同。请注意,前 256 个代码已定义为翻译成单个字符字符串,就像在压缩代码中一样。
代码使用
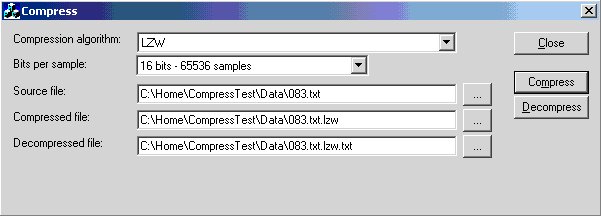
代码的使用非常简单,只需输入缓冲区及其长度,以及输出缓冲区及其长度。compress 函数包含一个额外的参数 nBitsPerSample,用于确定保存字典代码的位数,因此字典条目最多可达 2^nBitsPerSample。
bool CompressLZW(BYTE* pSrc, int nSrcLen, BYTE* &pDes,
int &nDesLen, int nBitsPerSample = 12);
bool DecompressLZW(BYTE *pSrc, int nSrcLen, BYTE *&pDes, int &nDesLen);
代码描述
我只有两个函数 CompressLZW 和 DecompressLZW,我将从第一个开始。
CompressLZW 函数
- 在此函数中,我正在扫描输入缓冲区
pSrc并向字典组件CBinaryTreeNode添加新条目。CBinaryTreeNode是一个二叉树类,它保存所有输入键的唯一实例,并且它以非常快的方式实现这一点,使用二叉搜索。要了解更多信息,您可以查看我在我的文章页面上的相关文章。 - 在输出缓冲区中,我在其前面加上一个 5 字节的头部:4 字节表示原始长度,1 字节表示每样本位数。
1:bool CompressLZW(BYTE *pSrc, int nSrcLen, BYTE *&pDes,
int &nDesLen, int nBitsPerSample = 12)
2:{
3: ...
4: CBinaryTree<CBuffer, CBuffer*, int, int> dictionary;
5: // keep first 256 IDs for ascii Samples
6: dictionary.Serial = 256;
7: // scan the input buffer
8: while(nSrcLen-- > 0)
9: {
10: ...
11: pNode = dictionary.Insert(&node, -1, pNode);
12: if(pNode->Count > 1 && nSrcLen)
13: // (repeated Sample)
14: nSample = pNode->ID, node.m_nLength++;
15: else
16: { // write last success Sample
17: *(DWORD*)(pDes+sizeof(DWORD)+1+
(nDesLen>>3)) |= nSample << (nDesLen&7);
18: nDesLen += nBitsPerSample;
19: // initialize node to next Sample
20: node.m_pBuffer += node.m_nLength-1;
21: node.m_nLength = 2;
22: // copy first byte of the node as a new Sample
23: nSample = *node.m_pBuffer;
24: ...
25: }
26: }
27: ...
28:}
我只包含了算法的主要要点。我认为第 17 行是唯一需要描述的行。
17: *(DWORD*)(pDes+sizeof(DWORD)+1+(nDesLen>>3)) |= nSample << (nDesLen&7);
它将样本代码复制到压缩缓冲区,但需要从正确的位开始复制。我知道有些人总是在脑海中颠倒移位运算符的功能,所以我将深入研究这一行。
sizeof(DWORD)+1:排除缓冲区头部。(nDesLen>>3):>>3表示除以 8 以达到要开始的正确字节。|=:避免覆盖前一个代码。(nDesLen&7):&7表示除以 8 的余数,以获得起始位。nSample << (nDesLen&7):向左移位代码以匹配目标缓冲区中的起始位。
DecompressLZW 函数
- 此函数比压缩函数更快,因为它不需要任何比较,例如在压缩过程中插入
CBinaryTree。 - 在此函数中,我正在扫描输入缓冲区
pSrc并从中获取代码,然后从字典中获取节点字符串指针。 - 我使用简单的
vectorSTL 模板来保存字典。 - 在输出缓冲区中,我在其前面加上一个 5 字节的头部:4 字节表示原始长度,1 字节表示每样本位数。
1:bool DecompressLZW(BYTE *pSrc, int nSrcLen, BYTE *&pDes, int &nDesLen)
2:{
3: // copy bits pre Sample
4: int nBitsPerSample = *(pSrc+sizeof(DWORD));
5: ...
6: // dictionary array
7: vector<CBUFFER *> dictionary;
8: // scan input buffer
9: while(nDesIndex < nDesLen)
10: {
11: // read sample code
12: nSample = (*(DWORD*)(pSrc+sizeof(DWORD)+1+
(nSrcIndex>>3)))>>(nSrcIndex&7) & (nMaxSamples-1);
13: nSrcIndex += nBitsPerSample;
14: // get code string node from the dictionary
15: if(nSample >= 256)
16: if(nSample-256 < (int)dictionary.size())
17: { // normal case, valid dictionary Sample
18: pNodeSample = dictionary.at(nSample-256);
19: nSampleLen = pNodeSample->m_nLength+1;
20: // copy dictionary node buffer to decompressed buffer
21: memcpy(pDes+nDesIndex, pNodeSample->m_pBuffer,
pNodeSample->m_nLength);
22: nDesIndex += pNodeSample->m_nLength;
23: }
24: else // out of range Sample
25: ...
26: else
27: nDesIndexSave = nDesIndex, *(pDes+nDesIndex++)
= (BYTE)nSample, nSampleLen = 2;
28: ...
29: // add current segment to the dictionary
30: dictionary.push_back(new CBuffer(node));
31: // increment next node pointer to the last char of the added Sample
32: node.m_pBuffer += node.m_nLength-1;
33: node.m_nLength = nSampleLen;
34: }
35: ...
36:}
与压缩一样,我只包含了算法的主要要点。我认为第 12 行是此时唯一需要描述的行。
12: nSample = (*(DWORD*)(pSrc+sizeof(DWORD)+1+
(nSrcIndex>>3)))>>(nSrcIndex&7) & (nMaxSamples-1);
它从压缩缓冲区复制样本代码,但需要从正确的位开始复制。
sizeof(DWORD)+1:排除缓冲区头部。(nSrcIndex>>3):>>3表示除以 8 以达到要开始的正确字节。(nSrcIndex&7):&7表示除以 8 的余数,以获得起始位。>>(nSrcIndex&7):右移到起始位以在位 0(靠近边缘)处获取代码。(nMaxSamples-1):nMaxSamples必须是 2 的幂,因为它由 2^nBitsPerSample或 1<<nPitsPerSample计算得出;因此,要将nMaxSamples用作掩码,我们需要减去 1。& (nMaxSamples-1):将其用作掩码,以删除超出代码限制(每样本位数)的额外位。
关注点
- 在压缩函数中,我使用二叉树来保存字典。我曾考虑使用哈希表,也许可以提高插入速度。无论如何,压缩 1MB 的时间不到 1 秒,解压缩时间不到 200 毫秒。
- 此代码的优点是字典索引的位数可变,压缩函数包含一个参数
nBitsPerSample。这意味着,如果字典中的条目数达到最大索引值的限制,我们需要清空字典并开始一个新的空字典。这可以在下面的 CompressLZW 函数部分看到。
int nMaxSamples = 1 << nBitsPerSample; ... while(nSrcLen-- > 0) { if(dictionary.Serial == nMaxSamples) { dictionary.RemoveAll(); dictionary.Serial = 256; } ... } - 与上一点一样,在解压缩函数中,从压缩缓冲区(第五个字节)获取
nBitsPerSample。同样,如果字典中的条目数达到最大索引值的限制,我们需要清空字典并开始一个新的空字典。这可以在下面的 DecompressLZW 函数部分看到。int nBitsPerSample = *(pSrc+sizeof(DWORD)); ... while(nDesIndex > nDesLen) { ... if(dictionary.size() == nMaxSamples-256) ClearDictionary(dictionary); ... } - 如第一个参考[1]中所述,LZW 压缩算法中有一个单一的例外情况,这给解压缩函数带来了一些麻烦。假设表中已定义一个由 (
string,char) 对组成的字符串,并且输入流随后看到一个 (string,char,string,char,string) 序列,或者我们可以说,如果编码算法读取了它在前一步添加到字典中的字符串。在解码过程中,此字符串尚未存在于字典中。字符流中一个字符串连续出现两次仅当其第一个和最后一个字符相等时才可能发生,因为下一个字符串总是以前一个字符串的最后一个字符开头。例如,在压缩过程中。Input string is "...JOEYNA...JOEYNJOEYNJOEY...". w k output index dictionary -------------------------------------------- JOEY N 288(JOEY) 300 JOEYN N A N 301 NA ... JOEYN J 300(JOEYN) 400 JOEYNJ JOEYNJ O 400(JOEYNJ) 401 JOEYNJO O E O 402 OE ...在解压缩算法中,它是这样的:
1:Input string is "...<288>NA...<300><400>O..." 2: w k output index dictionary 3: -------------------------------------------- 4: ... <288> JOEY 299 ...J 5: JOEY J J 300 JOEYJ 6: ... 7: ... <300> JOEYN 399 ...J 8: <400> O JOEYNJ 400 JOEYNJ 9: ...
问题出在第 8 行,因为要添加到字典中的新符号是 JOEYN 加上输入的字符,该字符是代码 400,而该代码尚未进入字典。所以我们需要一个特殊情况,即重复前一个符号的第一个字符作为字典条目的结尾,因此 (JOEYN?) 变为 (JOEYNJ)。为了处理这种情况,我们取前一个符号 JOEN 并以其第一个字符结尾。以下代码处理此情况。
bool DecompressLZW(BYTE *pSrc, int nSrcLen, BYTE *&pDes, int &nDesLen) { ... while(nDesIndex < nDesLen) { nSample = (*(DWORD*)(pSrc+sizeof(DWORD)+1+ (nSrcIndex>>3)))>>(nSrcIndex&7) & (nMaxSamples-1); nSrcIndex += nBitsPerSample; if(nSample >= 256) if(nSample-256 < (int)dictionary.size()) { // normal case, valid dictionary Sample nDesIndexSave = nDesIndex; ... } else { // out of range Sample nSampleLen = nDesIndex-nDesIndexSave+2; // copy previous decompressed Sample as a new one + ... memcpy(pDes+nDesIndex, pDes+nDesIndexSave, nDesIndex-nDesIndexSave); nDesIndex += nDesIndex-nDesIndexSave; // add first char of the previous decompressed Sample *(pDes+nDesIndex++) = *(pDes+nDesIndexSave); nDesIndexSave += nSampleLen-2; } else ... ... } ... }在此代码中,我仅使用变量
nDesIndexSave保存旧符号条目,以便在符号超出范围时使用。
源代码文件
LZW.cpp、LZW.h 和 BinaryTree.h。
更新
- 2005-01-20:我已解决了解压缩中的一个非常特殊的错误,如果您在此日期之前获取了代码,请更新。
- 2008-01-01:解决了大文件压缩的文件尾部不匹配错误。感谢“Wael AlGhool”。
- 2008-01-15:更新了压缩的伪代码。
参考文献
- Mark Nelson 的《LZW 数据压缩》,发表于 1989 年 10 月的《Dr. Dobb's Journal》。
感谢...
我非常感谢我的同事们在实现和测试此代码时给予我的帮助。(JAK)
