65.9K
CodeProject 正在变化。 阅读更多。
Home

二维空间中两个移动对象的拦截

Mike Oberberger
starIconstarIconstarIconstarIcon
emptyStarIcon
starIcon

4.97/5 (21投票s)

2015年5月14日

CPOL

22分钟阅读

viewsIcon

55053

downloadIcon

1051

计算一个速度向量，该向量允许第一个移动对象在给定已知位置和当前速度的情况下，在游戏或模拟环境中拦截第二个移动对象

Image of intercepting vectors

引言

这些信息将允许你确定一个物体（“追逐者”）必须移动的方向，以便它能够拦截目标物体（“跑步者”）。它假设你了解两个物体在二维空间中的位置。它假设你了解你的追逐者可以移动的速度。它假设你了解跑步者当前的速度和方向。

追逐者和跑步者都被抽象为平面上的点。这足以满足许多模拟和视频游戏场景。如果使用游戏对象的包围体进行碰撞检测，游戏对象之间的碰撞会比这个算法预测的稍早发生。

背景

在大多数视频游戏中，近似真实世界的物理现象就足够了。例如，由于计算机以离散方式运行（一个指令接一个指令），因此在**指令之间**发生的事情必须对许多事物进行近似。有时游戏通过完全跳过物理学来获得更好的效果，只是简单地允许物体的速度从0瞬间改变到*maxSpeed*，而无需关心力和惯性的物理学。这种物理学的暂停对于许多游戏来说是完美的——想象一下如果吃豆人每次转弯时都必须减速会怎样。

在本文中，我将描述一个寻找拦截点的过程，假设惯性和加速度被近似或忽略，并且游戏可以定期重新计算这个拦截点（如果需要，每帧游戏都会计算）。如果我们的游戏可以抛开物理学，允许追逐者的方向和速度瞬间设置（没有随时间变化的加速度），那么该算法是100%准确的（不是近似值）。

这里有一篇文章 文章链接，它提供了一个非常彻底的方法来做类似的事情。我对一种更简单的方法感兴趣，它在视频游戏中很有用。

这种方法大量使用了向量，在许多 其他 文章中都有详细描述。我将提供理解二维向量在此文章框架内如何使用的基础知识。

代码是用 C# 实现的，但（希望）很容易翻译成其他语言。

一些2D向量数学

注意——我在此承认向量有许多不同的用途，可以表示许多不同的事物，可以用许多不同的形式表达，等等等等。我希望通过省略进一步承认所有可能的不同使用或实现向量的方式来简化本文。

由于本文主要依赖简单的二维向量，我将回顾这个主题并澄清其中使用的符号。二维向量将由两个元素组成——x和y。这些是实数，但在包含的软件中使用时将由浮点值表示。

标量是只有大小而没有方向的量。标量值通常由基本类型表示，例如 `int`、`float` 等。标量“只是一个数字”——没有什么特别之处。我将使用双精度浮点数来表示标量。

向量是一个既有方向又有大小的量。通过对向量的 x 和 y 元素执行操作，可以推导出向量的方向和大小。X 和 y 是标量值，它们共同构成一个向量。重要的是要注意，x 和 y 的语义假设了一个 笛卡尔坐标系。使用一个 极坐标系，其中一个元素表示长度，另一个元素表示方向，也同样可行。我将从*存储的*笛卡尔坐标中*推导出*极坐标。

向量将用大写粗体变量表示（例如 **V**）。标量将用小写粗体变量表示（例如 **s**）。向量 **V** 的 x 和 y 分量将表示为 **V.x** 和 **V.y**。

向量可以是两种语义类型——位置（点）向量和速度向量。两者都以相同的形式表示，即一对 x 和 y 值。位置向量表示从*原点* (0,0) 到平面上一点的向量。这直接对应于对具有 (x,y) 坐标位置的基本理解。

速度向量表示方向和速度。它不位于二维平面上的任何“位置”。然而，它可以很容易地表示两个点向量之间的差异。速度向量表示一个点在*一个单位时间*内将移动多远以及朝哪个方向移动。速度向量的*大小*表示速度的*分量*。速度向量的*单位向量*表示速度的*方向*分量。

二维速度向量和二维位置向量的唯一区别在于语义。如何使用向量决定了它是什么。这与向量具有某种内在识别特征来确定它是位置向量还是速度向量的观念形成对比。它没有这种特征。

此图显示了两个位置向量 **P1** 和 **P2** 以及一个速度向量 **V**。这张图片的英语翻译是：如果一个游戏对象在点 **P1**，并且它以速度 **V** 移动，并且经过一个单位时间，那么该游戏对象将在点 **P2**。

在图中，**P1** 的值为 (2,-3)，**P2** 的值为 (-2,-1)。**V** 的值为 (-4,2)。此外，**V = P2 - P1**。这读作*从 **P1** 到 **P2** 的向量*。这两个项的顺序很重要。另请注意，对于某些人来说，将“目标”点减去“起始”点可能感觉“倒置”。

向量与标量有许多类似的算术运算，其中大部分都是直观的。我将展示本算法中使用的那些运算。

操作 (Operation) 符号 算法
加法 R = P + Q
$R.x = P.x + Q.x$
$R.y = P.y + Q.y$
减法 R = P - Q
$R.x = P.x - Q.x$
$R.y = P.y - Q.y$
标量乘法 **R =** c**P**
$R.x = cP.x$
$R.y = cP.y$

大小（“长度”）

 m = **|P|**
$m=\sqrt{P.x^2 + P.y^2}$
法线（“单位向量”） **R =** 归一化** (P)**
$R=\frac{1}{|P|}P$
点积 点积 **= P · Q**
$P\cdot Q = P.xQ.x + P.yQ.y$

前三个操作（加法、减法和标量乘法）是直观的。我不会在这里讨论它们。

**模长**运算表示向量的*长度*。该公式与计算两点之间欧几里得距离的公式相同。速度向量的*模长*是速度的*分量*。位置向量的模长是该点到原点的距离。两个位置向量之差的*模长*是两个位置之间的*距离*。

向量的**法线**等于向量与向量大小的倒数进行标量乘积。这也被称为*单位向量*，因为法线向量的长度将始终为1个单位（无论是英寸、像素、英里等任何“单位”）。*法线*表示速度向量的*方向*，就像*大小*表示速度向量的*速度*一样。计算位置向量的法线并不是很有用，但计算两个位置向量*之差*的法线可以非常有用。

点积

最后一个运算，即 **点积**，有时是最难理解的。点积与两个向量之间夹角的*余弦*有直接关系。在下图所示中，令 **A** 和 **B** 代表两个向量——请假装有箭头指向远离 **ϴ** 所表示的点。

在图中，**A** 和 **B** 在符号 **ϴ** 处共享一个共同点。这使得解释更容易，但这并非必需。为了解释，**A** 和 **B** 表示从共同点发出的向量。**ϴ** 表示这两个向量之间形成的角。**A** 和 **B** 的*点积*与角 **ϴ** 的余弦相关。

$\begin{aligned}A\cdot B=|A||B|\cos\Theta \end{aligned}$

这是一个非常重要的关系，因为它直接导致

$\begin{aligned}\cos\Theta=\frac{A\cdot B}{|A||B|}\end{aligned}$

... 并且 ...

$\begin{aligned}\Theta=\cos^{-1}\frac{A\cdot B}{|A||B|}\end{aligned}$

给定两个向量，很容易找到它们之间的夹角。最后一个方程很有趣，但对于我们的追逐者和跑步者来说并非必要。这个问题只需要角度的余弦。

关于点积的一个有趣之处在于，它允许计算两个向量之间夹角的余弦，而无需调用三角函数。计算点积比计算余弦快得多。即使你在一台 Haswell（约 2013 年）处理器上编写汇编语言，FMUL 和 FSQRT 指令也只需要 1 个时钟周期，而 FDIV 需要 1 或 2 个。然而，FCOS 单独就需要 110 个时钟周期。即使考虑延迟，FCOS 仍然慢得多。*参考：Agner Fog 的著作*。*诚然，这与本文有点无关，但我认为它很有趣。*

简要回顾余弦定理

该算法的核心组成部分是 余弦定理。在上图中，如果 A、B 和 C 被视为*三角形的边长*，则余弦定理指出

$\begin{aligned}C^2= A^2 + B^2 - 2AB\cos\Theta \end{aligned}$

该图对于 A、B 和 C 的具体含义有些模糊。当图在*向量* **A**、**B** 和 **C** 的点积的上下文中描述时，其上下文与在三角函数方面描述时不同。如果余弦定理重新表述为以与*点积*描述中相同的方式使用 A、B 和 C，则余弦定理变为

$\begin{aligned}|C|^2= |A|^2 + |B|^2 - 2|A||B|\cos\Theta \end{aligned}$

回想上面点积的定义

$\begin{aligned}A\cdot B=|A||B|\cos\Theta \end{aligned}$

显然，点积 $\( |A||B|\cos\Theta \)$ 等于更新的余弦定理的最后一项，从而得到一个新的方程

$\begin{aligned}|C|^2= |A|^2 + |B|^2 - 2(A\cdot B) \end{aligned}$

这产生了一个没有任何三角函数调用的余弦定理。

最后一个回顾主题——二次方程

一个*二次方程*的形式是

$\begin{aligned}ax^2+bx+c=0\end{aligned}$

其中 *x* 是未知值。为了根据 *x* 求解二次方程，我们可以使用 *二次公式*

$\begin{aligned}x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\end{aligned}$

如果二次方程有实数解（非复数），则二次公式将提供 x 的实数值。

至此，我应该有足够的信息来使用向量和余弦定理重新描述追逐者和跑步者的问题了。

2D 与 3D

在这个简单的场景中，追逐者和跑步者都将由二维平面上的点表示。这里描述的概念可以相当直接地转换为三维空间，因为整个过程都发生在一个平面内。通过考虑追逐者、跑步者以及等于跑步者位置加上其速度向量的某个非零倍数的第三个点，所有这些都在三维空间中，你就可以拥有定义三维空间中任何平面所需的三个唯一点。

由此，对所有坐标应用变换矩阵将产生3D和2D之间必要的转换。然而，这不是本文的主题。

代码背后的数学

设置问题

我选择“追逐者”和“跑步者”，因为在我解决这个问题时，我一直想到“大灰狼”和“BB鸟”。众所周知，大灰狼从来没有真正抓到过BB鸟，但我假装他可以。

所以，想象一下追逐者（大灰狼）看到了跑步者（BB鸟）。追逐者可以知道跑步者的速度以及跑步者前进的方向。追逐者也知道他自己能跑多快。通过将自己置于正确的位置，即使追逐者比跑步者慢，仍然可能存在一个追逐者可以移动的方向以拦截跑步者。

首先，让我们描述在使用此算法之前已知的变量。如您所见，我对图片应用了我的特殊版权规避技术。

**PC** = 追逐者的位置，作为位置向量（x 和 y 坐标）
**PR** = 跑步者的位置，作为位置向量
**SC** = 追逐者的速度（标量）（尚未显示）
**VR** = 跑步者的速度向量（速度和方向）

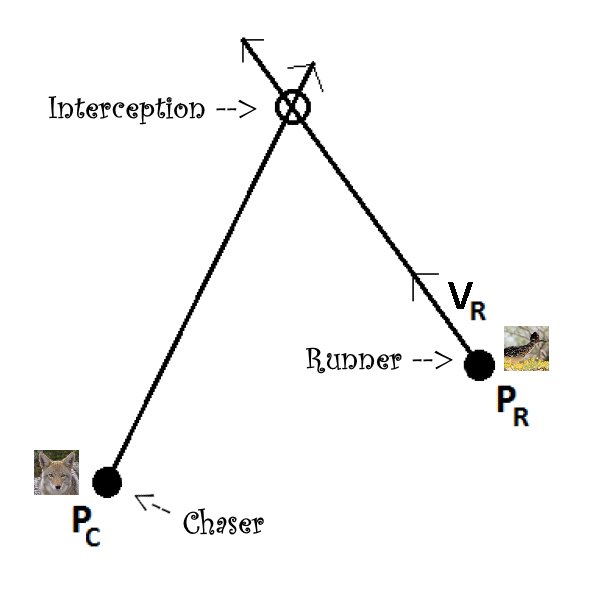
根据这些给定的输入，可以很容易地计算出其他一些基本信息。

**SR** = 跑步者的速度（一个标量），等于 **VR** 的大小（未显示）
**d** = 追逐者和跑步者之间的初始距离
**D** = *从*跑步者*到*追逐者的向量

在前面的图片中，显然出现了一个三角形。新添加的边是一个向量 **D**，它等于 **PC - PR**。还显示了三角形一条边的长度，标记为“**d**”。这只是跑步者和追逐者之间的距离。它可以描述为向量 **D** 的**大小**，可以写成 |**D**| 或 |**PC - PR**|。

图片尚未显示跑步者或追逐者的速度。这是因为速度在图形化显示之前需要更多的上下文。

但另外两条看起来构成三角形的线呢？它们的长度呢？

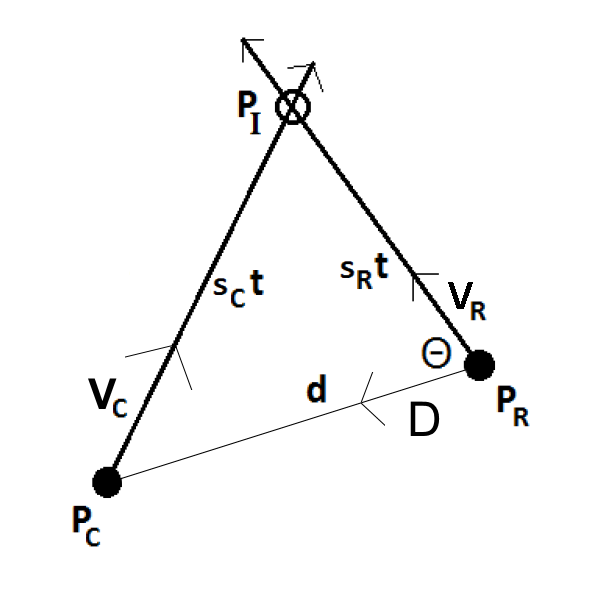
*注：在此图中，三角形*内部*的符号都表示*标量值*（距离或角度），而三角形*外部*的符号表示*向量*（位置或速度）。*

此图中新增了三个元素。首先是角度 **ϴ**。**ϴ** 是向量 **D** 和 **VR** 之间的角度。回想我们的*点积*，我们知道

$\begin{aligned}\cos\Theta = \frac{D\cdot V_R}{|D||V_R|}=\frac{D\cdot V_R}{ds_R}\end{aligned}$

它现在还不是完全有用，但请记住它以备后用。**cos(ϴ)** 现在已经用已知值定义了。

之前图中可疑地缺失的速度分量已添加到此图中。**PC** 和 **PI** 之间向量的*长度*将是追逐者的速度 **sC** 乘以 **t**。**t** 是拦截所需的时间。**t** 是一个未知数——它将是我们未来步骤中“求解”的值。此时，我们只知道拦截将需要*一定时间 **t*** 发生。这提供了三角形第二条边的长度。

既然我们假设会发生拦截，并且拦截会在未来的某个时间点 **t** 发生在点 **PI**，我们就知道必须将跑步者的速度 **sR** 乘以相同的时间 **t**，才能得到*跑步者*在到达 **PI** 之前必须行进的距离。这提供了三角形最后一条边的*长度*。

请记住，此算法的目标是计算以下值：

**VC** = 追逐者的速度向量（我们知道其速度，我们需要其方向）
**PI** = 追逐者和跑步者之间的拦截点
**t** = 拦截所需时间
...如果两者甚至可能拦截的话！

在本节中，假设追逐者将成功拦截跑步者。描述数学原理后，我将解释如何判断何时无法进行拦截。这可能是由于几个不同的原因——追逐者的速度为0，追逐者太慢且已经落后等等。很容易精确检测出追逐者无法拦截跑步者的确切原因。

我们已经掌握了解决问题所需的所有设置和信息！

运用已知信息

问题中真正的未知变量是 **t**，即拦截发生所需的时间。如果我们知道 **t**，那么我们知道上面图片中的所有其他信息。**PI** 等于 **PC + VCt** 和 **PR + VRt**。当 **PR + VRt** 已知时，通过将这两个方程设置为相等并求解 **VC**，可以很容易地找到 **VC**。

让我们首先回顾一下算法的*输入*。这些值不需要计算——它们是提供的。

变量 计算 描述
PC 鉴于 追逐者的当前位置
PR 鉴于 跑步者的当前位置
SC 鉴于 追逐者能够达到的速度
VR 鉴于 跑步者的当前速度和方向

有一些非常基本的值是直接从这些给定值计算出来的。

变量 计算 描述
D
$P_C-P_R$
 从跑步者到追逐者的向量
d
$|D|$
 追逐者和跑步者之间的距离
SR
$|V_R|$
 跑步者的速度
cos(ϴ)
$\frac{D\cdot V_R}{ds_R}$
 不需要实际角度——只需要它的余弦

所有重要内容现在都已定义。接下来，需要将余弦定理应用于边长分别为 **SCt**、**SRt** 和 **d** 的*三角形*。回顾余弦定理：

$\begin{aligned}C^2= A^2 + B^2 - 2AB\cos\Theta \end{aligned}$

查看图片，应该很明显A、B和C的赋值如下：

$C=s_Ct$
$B=s_Rt$
$A=d$

...将这些变量代入余弦定理方程

$(s_Ct)^2= (s_Rt)^2+d^2-2ds_Rt\cos \Theta$

...然后展开平方项

$s_C^2t^2= s_R^2t^2+d^2-2ds_Rt\cos \Theta$

...利用简单的代数，t 的系数可以移动，形成以下方程

$(s_C^2-s_R^2)t^2+2ds_R\cos\Theta t-d^2=0$

...这显然是一个二次方程，如本文前面所述

$\begin{aligned}ax^2+bx+c=0\end{aligned}$

...其中，在这种情况下，变量 a、b 和 c 取以下值：

$a=s_C^2-s_R^2$
$b=2ds_R\cos\Theta$
$c=-d^2$
$x=t$

查看“b”分量，请回顾上面所示的 **cos(ϴ)** 的计算。我将使用这两个公式重新编写“b”分量：

$\cos\Theta=\frac{D\cdot V_R}{ds_R}$
$b=2ds_R\cos\Theta$
$b=2ds_R\frac{D\cdot V_R}{ds_R}$

...消去分母...

$b=2(D\cdot V_R)$

重要的是要注意，此时所有这些值既是标量又是已知值。当这些值代入*二次公式*时，我们得到 *t* 的值，这些值准确地告诉我们拦截将*何时*发生。

$\begin{aligned}t=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\end{aligned}$
$a=s_C^2-s_R^2$
$b=2(D\cdot V_R)$
$c=-d^2$

一旦我们知道拦截发生的时间，我们就可以将这个时间 *t* 应用于跑步者的速度向量，以获得拦截点。

$P_I=P_R+V_Rt$

已知 **PI**，我们可以利用 **sC** 和 **PI** 与 **PC** 之间的向量来得到 **VC**。

$P_I=P_C+V_Ct$
$V_C=\frac{P_I-P_C}{t}$

现在计算出了所有三个有趣的值：追逐者需要奔跑的方向，追逐者和跑步者之间的拦截点，以及拦截所需的时间。问题已经*大部分*解决了。那么边缘情况以及无法拦截时会发生什么呢？

二次公式结果的解释

二次公式可以返回两个 *t* 值，因为满足二次方程的 *t* 可能有两个正确值。此外，方程可能没有实数值解。

当二次公式的这一部分

$b^2-4ac$

为负数时，方程没有实数值解。这立即意味着在提供的信息下，追逐者无法拦截跑步者。

同样，当 t 的两个可能值都为负数时，这也意味着追逐者拦截跑步者的唯一可能机会是回到过去，在过去拦截跑步者。两个 t 值都为负数意味着没有拦截的机会，因为我们不假装时间旅行是可行的。

当一个 *t* 值为负，另一个为正时，则使用正的 *t* 值来确定 **PI**。负值被忽略——它表示追逐者必须回到过去才能拦截跑步者的概念。

当 *t* 的两个值都为正时，使用两个值中*较小*的一个来计算 **PI**。假设追逐者希望尽早拦截。这通过以下图示可视化：

由于追逐者被假定具有*恒定速度*，他可以在两个地方拦截跑步者。注意：如果允许追逐者选择任意慢的速度，那么拦截可能发生在图中所示的两个箭头之间的任何位置。

余弦定理和/或二次公式不适用的边缘情况

边缘情况 #1：追逐者已经追上了跑步者 (PC ≈ PR)

这很简单——拦截点是 **PC**（或 **PR**），时间是 0，追逐者的速度向量是 (0,0)。

边缘情况 #2：追逐者的速度为 0

当追逐者无法移动时，显然无法发生拦截（假设我们首先检查了边缘情况 #1）。

边缘情况 #3：跑步者的速度为 0

当跑步者无法移动时，计算会退化为这些简单的方程：

$P_I=P_R$
$t=\frac{d}{s_R}$
$V_C=-s_R\frac{D}{d}$

边缘情况 #4：跑步者的速度等于追逐者的速度

如果追逐者的速度等于跑步者的速度，那么就不再是二次方程，因为“a”值变为零。发生这种情况时，会出现一个线性方程，并且不能使用二次公式（它会尝试除以零）。我在此软件中的二次求解器会检测到这种情况，并将二次公式替换为：

$t_1=t_2=-\frac{c}{b}$

当它检测到“a==0”时。算法实现依赖于这种自动替换，而不是显式检查相等的速度。

本文的数学和理论部分现已完成。接下来是软件。

算法的 C# 方法实现

直接进入正题，这是算法本身的 C# 代码。它的编写方式让读者应该能够理解其原理，而不必完全了解所有支持和辅助类、属性和方法。它还通过将“边缘情况”和“假设拦截”情况以一种合理的方式编织在一起，遵循了本文上一节中执行的步骤。

/// <summary>
/// Called internally to calculate the interception data.
/// </summary>
private void SetResults()
{
    // Don't re-calculate if none of the input parameters have changed.
    if (m_calculationPerformed)
        return;

    // Make sure all results look like "no interception possible".
    ClearResults();

    // Set this to TRUE regardless of the success or failure of interception. This
    // prevents this routine from doing anything until one of the input values has been
    // changed or the application calls ClearResults()
    m_calculationPerformed = true;

    // If the inputs are invalid, then everything is already set for a "no interception"
    // scenario.
    if (!HasValidInputs)
        return;

    // First check- Are we already on top of the target? If so, its valid and we're done
    if (ChaserPosition.AreSame( RunnerPosition ))
    {
        m_interceptionPossible = true;
        m_interceptionPosition = ChaserPosition;
        m_timeToInterception = 0;
        m_chaserVelocity = SVector2d.Zero;
        return;
    }

    // Check- Am I moving? Be gracious about exception throwing even though negative
    // speed is undefined.
    if (ChaserSpeed <= 0)
        return; // No interception

    SVector2d vectorFromRunner = ChaserPosition - RunnerPosition;
    double distanceToRunner = vectorFromRunner.Length;
    double runnerSpeed = RunnerVelocity.Length;

    // Check- Is the Runner not moving? If it isn't, the calcs don't work because
    // we can't use the Law of Cosines
    if (runnerSpeed.IsClose( 0 ))
    {
        m_timeToInterception = distanceToRunner / ChaserSpeed;
        m_interceptionPosition = RunnerPosition;
    }
    else // Everything looks OK for the Law of Cosines approach
    {
        // Now set up the quadratic formula coefficients
        double a = ChaserSpeed * ChaserSpeed - runnerSpeed * runnerSpeed;
        double b = 2 * vectorFromRunner.Dot( RunnerVelocity );
        double c = -distanceToRunner * distanceToRunner;

        double t1, t2;
        if (!CMath.QuadraticSolver( a, b, c, out t1, out t2 ))
        {
            // No real-valued solution, so no interception possible
            return;
        }

        if (t1 < 0 && t2 < 0)
        {
            // Both values for t are negative, so the interception would have to have
            // occured in the past
            return;
        }

        if (t1 > 0 && t2 > 0) // Both are positive, take the smaller one
            m_timeToInterception = Math.Min( t1, t2 );
        else // One has to be negative, so take the larger one
            m_timeToInterception = Math.Max( t1, t2 );

        m_interceptionPosition = RunnerPosition + RunnerVelocity * m_timeToInterception;
    }

    // Calculate the resulting velocity based on the time and intercept position
    m_chaserVelocity = (m_interceptionPosition - ChaserPosition) / m_timeToInterception;

    // Finally, signal that the interception was possible.
    m_interceptionPossible = true;
}

该方法试图在不同点证明无法发生拦截。当这一点被证明时，例程会立即返回。我向那些坚持每个方法应该只有一个出口点的纯粹主义读者致歉——我并不总是同意你们，但我尊重你们的意见。

关于包含此方法的类，需要注意的事项：

  1. 该类有四个读/写属性，每个对应一个输入值：`ChaserPosition`、`ChaserSpeed`、`RunnerPosition` 和 `RunnerVelocity`。
  2. 该类有三个只读属性用于主要输出：`ChaserVelocity`、`TimeToInterception` 和 `InterceptionPoint`。访问这些值中的任何一个都会触发数据的重新计算，**当且仅当**任何输入数据已更改时。
  3. 该类有一个只读属性 `InterceptionPossible`，它表示对于给定的输入，拦截是否可能。
  4. 该类有一个只读属性 `HasValidInputs`，当所有输入值都设置为有效值时，该属性为 TRUE。默认情况下，它们具有无效值，并且应用程序需要设置所有这些值。
  5. 所有属性都是不可变的值类型。如果不是，这种使用模式将不起作用。

关于向量类的一些注意事项

  1. 它是一个不可变的值类型。
  2. 它具有算术使用模式（例如 P + Q）以及流畅使用模式（例如 P.AddTo( Q )）。
  3. 通过将 X 或 Y 设置为 NaN（或无穷大），它支持“无效值”。

还有另一个名为 `CMath` 的辅助类，其中包含以下内容：

  1. 检测“接近”的双精度值。如果您不喜欢我对“接近”的定义，请随时将其更改为适合您的值。
  2. 一个二次方程求解器

使用该类

在下面的示例中，包含拦截算法的类的使用方式如下：

var intercept = new CInterceptCalculator2d()
{
    ChaserPosition = coyote.Position,
    ChaserSpeed = coyote.Speed,
    RunnerPosition = roadrunner.Position,
    RunnerVelocity = roadrunner.Velocity
};

if (!intercept.InterceptionPossible)
    Console.Writeline( "The coyote is too slow to intercept the roadrunner" );

coyote.Velocity = intercept.ChaserVelocity;
// could look at intercept.TimeToInterception    
// could look at intercept.InterceptionPoint

类 `CInterceptCalculator2d` 维护一个内部状态，每次其输入属性之一发生变化时都会检测到。当查询其中一个输出属性时，它将检查自上次计算以来是否有任何输入发生变化，并在必要时重新计算。应用程序无需调用任何特殊方法来执行计算——只需在设置所有输入值后查询一个输出值，即可获得正确答案。

如果输入值未全部设置，则输出值将等于 `SVector2d.NotAVector`。以下代码可用于检测此情况：

var intercept = new CInterceptCalculator2d()
{
    ChaserPosition = coyote.Position,
    ChaserSpeed = coyote.Speed,
    RunnerVelocity = roadrunner.Velocity // runner position not set!
};

assert( ! intercept.ChaserVelocity.IsAVector )
assert( intercept.InterceptionPoint == SVector2d.NotAVector )

模拟器 - ZIP 文件内容

本文附带了一个模拟器，它可视化了拦截算法的使用。这是一个 Windows Forms 应用程序。运行时，用户会看到一只“鸽子”（一个白点）在屏幕顶部移动。他还会看到一把“枪”（一个红点）和枪管（一条红线）。枪管将始终指向需要发射子弹（一个绿点）的位置，以便击中移动的鸽子。

用户可以拖动枪支在屏幕上移动，以查看这如何影响枪管的角度。当用户按下“F”键时，子弹将从枪支中射出，沿直线飞行直到击中鸽子。如果鸽子在子弹飞行过程中改变方向，子弹显然会射失鸽子。

CInterceptCalculator.cs

这是主要的拦截计算器对象。

SVector2d.cs

这个文件包含了我的向量类的全部内容。里面有一些东西不是这个应用程序立即使用的，但希望你会从中发现一些有趣的东西。

CMath.cs

多年来我编写的辅助和便利方法的集合。主要为此应用程序提供二次公式和“IsClose”功能。

CMovableObject.cs, CCircle.cs, CRectangle.cs

这些是模拟中使用的可移动对象。矩形在此模拟中未使用。

FInterceptSimulation.cs

这是包含模拟的主 Windows Form。这里没有 MVC 模式——这是一个简单的测试程序，用于展示拦截算法的功能。

如果这些文件中的任何代码对您不清楚，请随时提问，我将很乐意回答您的问题。

关注点

我为一门应邀开发的视频游戏人工智能课程撰写了本文的实质内容。这是该课程的主题之一。我以前从未真正思考过拦截的原理——我一直认为这是一个容易解决的问题（当然，“容易”在这里是个模糊的词……）。

虽然本文中提出的任何单个概念都没有任何“难度”，但将它们整合在一起是一次有趣的练习。从那时起，我将这个主题作为另一门视频游戏开发课程的客座讲师，现在已经对其进行了完善，以供 CodeProject 读者阅读。

© . All rights reserved.