按升序排列整数

引言

本文是文章“按2d曲线排序”的后续文章。本文讨论了在 O(n) 中寻找排序算法。

目前，这种算法不存在，因为最佳复杂度是O(n log(n))。

一个想法

我认为可以通过乘以一个我称为M的数值来找到给定数字的后继者。
存在一个代数公式来展示这个定义。

例如，获取给定数字的后继者可以是

1. 2 = 1 * M
2. 3 = 2 * M
3. 4 = 3 * M
4. 5 = 4 * M
5. n + 1 = n * M

然后，剩下的是

想法是寻找一个代数函数，使得数字n乘以这个函数得到最接近n的后继者。如果所有元素都已经排序，则M的值将是最准确的。

每当我在列表末尾添加一个新的整数时

• 列表的前一个元素
• M的浮点值
• 之前的问题

但我希望得到一个M函数，它考虑到列表的元素。为了找到一个数字的后继者，这个后继者必须在这个给定的列表中找到。因此，M的浮点值是在该数字添加到列表后获得的准确值。

目标

我们希望对整个列表进行排序，因为它的复杂度是O (n)。为了获得这样的复杂度，我们假设存在一个公式可以给出所有后继者。

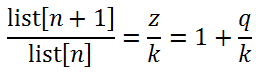
1. 如果列表已经按升序排序，则 q >= 0。
2. 但是，如果列表没有完全按升序排序，则 q < 0。

示例

为了表达一个考虑到所有先前值的数学方程式，这个方程式对M的所有排列给出相同的值。这意味着排列占用未排序的列表。只有一个顺序，即收敛于排序列表的排列序列。

值的总和

假设我有n个值 。如果我将所有值相加，那么的任何排列都会得到相同的结果。

现在，通过添加每个，我们假设可以将这个总和乘以一个给定的数字，并且这个结果等于一个特定的，它由该的索引位置标识。这个提议的演示可能是准确的，我们尝试选取和来查找它们的值。为此，我们希望假设将总和乘以一个数字s将给出或。

我们存储一个元素对的列表，这些元素保留了元素和先前计算的值。在每次迭代中，我们计算n的值。此值是完整模式的数量。

算法

[<<[

    print("start"),
    u = [ 3, 4, 20, 5.1, 6, 7, 20, 22 ],
    sum = 0,
    foreach(x from u) {
       sum = sum + u(x)
    },
    fun getIndex(sum, x) {
       output(1/((sum-x)/x+1))
    },
    z = [],
    foreach(x from u) {
       z = z getIndex(sum, u(x))
    },
    print(z),
    sum2 = 0,
    foreach(x from z) {
       sum2 = sum2 + z(x)
    },
    print(sum2),
    print(z.length),
    r = [],
    fun toInt(x) {
       n = 0,
       fun selectIndice(t) {
           p = [ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ],
           select {
               break {},
               default {
                  count = 9,
                  while(count >= 0) {
                     if (p(count) <= t) {
                        t = p(count),
                        jump "break"
                     },
                     count = count - 1
                  }
               }
           },
           output(t)
       },
       count = 1,
       while(x >= 1) {
          t = selectIndice(x % 10),
          x = (x-t) / 10,
          n = n + t*count,
          count = count * 10
       },
       output(n)
   },
   foreach(x from z) {
       k = z(x) * sum / 22 * z.length * z.length,
       print(k),
       m = toInt(k),
       print(m),
       r = r m
   },
   print(r)
]>>]

输出是：

8,11,58,14,17,20,58,64

这些数字是数组中的基数位置，因为其大小为 64 个项目。

历史

• 2022 年 10 月 24 日：初始版本