无数组数值螺旋模式
如何生成一个不使用数组的螺旋数值模式

图片 0 - 控制台屏幕上的 10 维螺旋模式
引言
该程序来自 QA 中的这个问题:在 C# 程序中制作模式。
虽然直接(且直观)的解决方案使用数组来跟踪已填充的位置,但这里提供的解决方案没有使用数组,从而实现了 O(1) 的空间复杂度,而不是 O(N^2)。
该程序的源代码已在链接页面上提供,这里我将展示导致该算法的“思路”。
想法
为了提供一个无数组的解决方案,有必要将每个数字与其在屏幕上的位置相关联,也就是找到映射
(x,y) -> n
其中
(x,y)是模式中数字的坐标,在一个“合适的”坐标系中。n是数字本身。
让我们goto细节...
问题
给定一个维度(例如 5),在控制台上生成一个螺旋模式,如下面的图片所示。
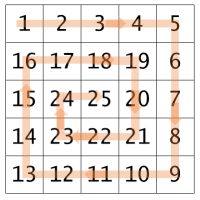
图片 1 - 维度 5 螺旋模式
反向问题
现在考虑以下“反向”问题

图片 2 - 维度 5 反向螺旋模式
当然,这非常等价:解决反向问题实际上解决了原始问题。
坐标系
一个“合适的”(即方便的)坐标系如图 3 和图 4 所示。

图片 3 - 合适的坐标系

图片 4 - 坐标系应用于奇数(左侧)和偶数(右侧)模式维度
这种系统很方便,因为它突出了系统的对称性,并且很好地适用于奇数和偶数模式维度。
值得注意的是,数字的位置(块)有
- 在奇数维度的模式中,偶数坐标为
.., -2, 0, 2, ..(参见图 4 的左侧) - 在偶数维度的模式中,奇数坐标为
.., -3, -1, 1, 3, ..(参见图 4 的右侧)
距离
在这种坐标中,一个有用的量是distance,定义如下
d(x,y) = max(abs(x), abs(y))
因此,例如
d(-3, 5) = 5d( 2, 2) = 2d( 2,-5) = 5
算法
现在,回到反向算法(请原谅双关语),让我们尝试找出如何将数字 18 分配到位置 (4,-2)。
解决方案是计算从中心开始,沿着反向模式,到所选坐标的块数。
图片 5 清楚地表明有两个贡献
- 内正方形(黄色块)
- 部分环(橙色块)
计算内正方形贡献很简单:(D-1)^2 块(其中 D = d(4,-2) = 4 是距离)。

图片 5 - 位置 (4,-2) 处数字的贡献

图片 6 - 内正方形和部分环贡献,在奇数和偶数维度模式中
部分环贡献更加困难。 根据位置的不同,可能存在四种情况(参见图片 7、8)
- 情况 A:“在底部的某个地方”
- 情况 B:“在顶部的某个地方”
- 情况 C:“在左侧的某个地方”
- 情况 D:“在右侧的某个地方”

图片 7 - 部分环贡献,情况 A, B

图片 7 - 部分环贡献,情况 C, D
以下代码段中显示了这些情况的公式
public static int ring_contribution(int d, int x, int y)
{
if (y == -d)
return (d - 1) + (d + x) / 2; // Case A, somewhere in the bottom
else if (y == d)
return (d - 1) + 2 * d + (d - x) / 2; // Case B, somewhere in the top
else if (x == -d)
return (d - y) / 2 - 1; // Case C, somewhere in the left
else
return 2 * d + (d + y) / 2 - 1; // Case D, somewhere in the right
}
将内正方形和部分环的贡献相加,可以得出反向问题的预期结果,进而得出原始问题的结果。
关注点
我相信这没有什么用处。 然而,再次痛打落水狗对我来说很有趣。
历史
- 2018 年 11 月 19 日 - 首次发布
