带有交互式地图的在线地理编码器
用于查找地理坐标并在必应地图上应用它们的 Web 应用程序
引言
地理坐标提供了一种统一的方法来识别地球上的任何地点。城市街道可能会更改名称和编号,但通用的坐标系不受日常虚荣和时间挑战的影响,可在行星级别上呈现永久性的时不变值。通常,地理坐标系包括经度、纬度和海拔(高度),但最常用的是前两个,即经度/纬度。它们可以用度:分:秒(所谓的DMS)格式或十进制度(DD)格式(应用程序中使用)表示。
地理坐标可以通过全球定位系统(GPS)设备获得,但这种技术需要在感兴趣的点进行物理存在。作为替代方案,可以使用地理编码软件应用程序(或简称地理编码器或地理定位器)将邮政地址转换为相应的经度/纬度对。这种地理编码器与由Microsoft Bing™技术驱动的交互式在线地图结合使用,允许不同的视图、全景和缩放;它可以在线完全免费使用[1],同时服务于实用和教学目的(无需注册)。
用法
使用方法相当简单直观:为了获得感兴趣的地理点的经度/纬度信息和地图,无论是在美国还是在世界范围内,请按照以下步骤操作
- 打开Web浏览器并导航到地理编码器
- 在搜索框中输入邮政地址,然后单击“查找”屏幕按钮。注意:美国的地点只需通过其邮政编码即可识别
- 屏幕重新加载完成后,可能需要几秒钟,您应该能够看到感兴趣的点的经度/纬度以及相应的Bing地图。您可以选择首选的地图视图模式(道路、航空或鸟瞰),调整缩放级别(从1到19)并执行全景功能
多语言支持
在线地理编码器具有多语言功能,可以接受多种外语的搜索查询:西班牙语、德语、意大利语、法语、俄语、希腊语等。以下是一些示例测试结果,对应于世界地标,以原始语言输入搜索查询
- Metropolitan Museum, New York | Lat: 40.779437/Lon: -73.963244
- Grand Central Terminal, NY | Lat: 40.752726/Lon: -73.977229
- Colosseo, Roma | Lat: 41.89021/Lon: 12.492231
- Ακρόπολη Αθηνών | Lat: 37.971532 /Lon: 23.725749
- Brandenburger Tor, Unter Der Linden | Lat: 52.516275 /Lon: 13.377704
- Champs-Elysées, Paris | Lat: 48.869576/Lon: 2.30825
- Eiffel Tour, Champs De Mars | Lat: 48.85837/Lon: 2.294481
- Museo del Prado, Madrid | Lat: 40.413782/Lon: -3.692127
- Cappella Sistina, Rome | Lat: 41.902947/Longitude: 12.454484
- Музей Эрмитаж, Санкт Петербург | Lat: 59.939832/Lon: 30.31456
演示
以下屏幕截图演示了具有交互式Bing地图的多语言地理编码器的用法(参见图1-4)
图1. 纽约哥伦布圆环广场,地理坐标(距纽约市的距离从此点计算)
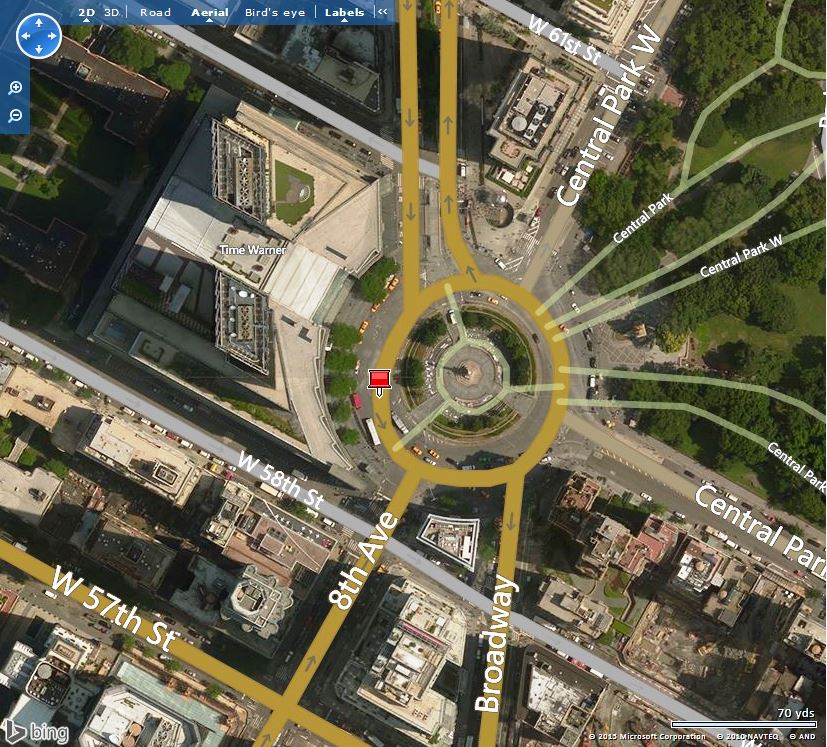
图2. Bing地图上的纽约哥伦布圆环广场,示例屏幕截图(航空视图模式)

图3. 德国柏林勃兰登堡门的坐标

图4. Bing地图上的勃兰登堡门(鸟瞰视图模式)
关注点
计算地球表面上两个地理点之间的大圆(正距)距离是常见的GIS任务。它可以通过使用下面列出的球面地球投影算法来完成[2]
/*****************************************************************************************
Module : GIS.cs
Description : Calculate distance between two geo-points on surface
*****************************************************************************************
Author : Alexander Bell
Copyright : 2011-2015 Infosoft International Inc
*****************************************************************************************
DISCLAIMER : This Module is provided on AS IS basis without any warranty
*****************************************************************************************
TERMS OF USE : This module is copyrighted. Please keep the Copyright notice intact.
*****************************************************************************************/
using System;
namespace BusNY
{
internal enum UnitSystem { SI = 0, US = 1 }
internal static class GIS
{
#region internal: properties (read-only)
internal static double EarthRadiusKm { get {return _radiusEarthKM;} }
internal static double EarthRadiusMiles { get { return _radiusEarthMiles; } }
internal static double m2km { get { return _m2km; } }
internal static double Deg2rad { get { return _toRad; } }
#endregion
#region private: const
private const double _radiusEarthMiles = 3959;
private const double _radiusEarthKM = 6371;
private const double _m2km = 1.60934;
private const double _toRad = Math.PI / 180;
#endregion
#region public Method: Spherical Earth projection
public static double DistanceSEP(double Lat1,
double Lon1,
double Lat2,
double Lon2,
UnitSystem UnitSys ){
try
{
double _radLat1 = Lat1 * _toRad;
double _radLat2 = Lat2 * _toRad;
double _dLat = (_radLat2 - _radLat1);
double _dLon = (Lon2 - Lon1) * _toRad;
double _a = (_dLon) * Math.Cos((_radLat1 + _radLat2) / 2);
// central angle, aka arc segment angular distance
double _centralAngle = Math.Sqrt(_a * _a + _dLat * _dLat);
// great-circle (orthodromic) distance on Earth between 2 points
if (UnitSys == UnitSystem.SI) { return _radiusEarthKM * _centralAngle; }
else { return _radiusEarthMiles * _centralAngle; }
}
catch { throw; }
}
#endregion
}
}

