从线性索引到上三角矩阵索引

Maniezzo

5.00/5 (3投票s)

2023年9月20日

公共领域

3分钟阅读

7913

114

几行代码，用于从线性化数组中获取上三角矩阵（包括主对角线）的 i-j 索引。

引言

“如果主对角线以下的条目都为零，则方阵称为上三角矩阵”（维基百科），因此包括主对角线。

这肯定是我自己的一个不足，可能是懒惰，但是稍微浏览了一下用于将一维线性索引转换为二维上三角索引的公式，我发现很多页面提出的公式都没有考虑主对角线（例如，这个），但是很少有人考虑它。好吧，人们可以使用假的行/列数，但那是不优雅的，不是吗？所以我认为最好自己推导公式，这本身并不是一件伟大的事情，并把它们放在这个技巧中。也许其他人会发现它们有用，或者可能我没有看到错误，并且有人会指出它。

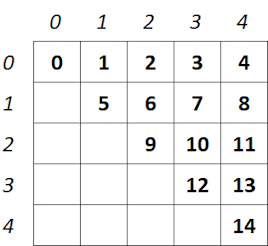
这个想法是，例如，有一个包含 15 个单元格的数组（例如，[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14]），这些单元格在概念上对应于下图所示的二维上三角矩阵的单元格。主对角线以下的所有空白单元格都为 0。例如，我需要推导出数组中索引为 10 的单元格在矩阵中的索引为 2,3。

Upper triangular matrix with linear indices

推导

逐步演练

假设二维矩阵有 $n$ 行（和 $n$ 列），因此有 $n^2$ 个单元格，它们都在主对角线以下为 0。第一个任务是确定每一行 $i, 0\leq i \lt n$ 的第一个一维索引 $k$。请注意，这只需从总单元格数中减去到第 $i$ 行的单元格数中减去到该行的主对角线以下的单元格数即可获得。这意味着所需的索引 $k$ 可以获得为

$k = i\cdot n - \frac{i(i-1)}{2}$

或者，等效地（请原谅我的咬文嚼字）

$2k = 2i\cdot n - i^2 + i$

因此

$i^2 - (2n+1)i +2k = 0$

解决为

$i = \frac{2n+1 \pm \sqrt{ (2n+1)^2 - 8k}}{2}$

得到

$i = \frac{1}{2}\left( 2n+1 \pm \sqrt{4n^2 + 4n -8k +1} \right)$

其中只需要考虑正分量。

有了索引 $i$，然后通过从 $k$ 中减去到对应行的第一个元素的所有元素，很容易得到索引 $j$

$j = k - \left( i\cdot n - \frac{i(i-1)}{2} \right)$

这也允许通过拥有 $i$ 和 $j$ 来获得 $k$。

已实现代码

实际上没有必要展示两行代码，但这里是。演示项目要求输入 n 并编写上三角矩阵，其中单元格已通过这两行放置

//
// 2D index computation
//
i = (int) (0.5*(2*n+1-Math.Sqrt(4*n*n + 4*n - 8*k + 1)));
j = (int) (k - (i*n - 0.5*i*i - 0.5*i));

这是 C#，但当然，只需在这里和那里更改几个括号，你就可以在 Python、C++... 中得到等效的代码

额外细节

最后一个细节。您可能有一个线性数组，并想知道该数组保存的上三角矩阵的 2D 矩阵的行/列数是多少。好吧，如果数组的单元格数为 $m$，那么这个数字必须满足方程

$m = \frac{n(n+1)}{2}$

因此 $2m = n^2 + n$ 或 $n^2 + n - 2m =0$，因此

$n = \frac{-1 \pm \sqrt{1+8m}}{2}$

你没有得到一个正整数？你一开始就没有正确的单元格数。

结论和关注点

这个技巧介绍了用于计算将线性数组重塑为上三角矩阵时（即，主对角线以下的所有单元格都为零的 2D 方阵）单元格索引所需的公式的简单推导。此选项比预期的更通用，例如，它提供了一种在内存中存储对称矩阵的有效方法。

历史

2023 年 9 月 20 日：初始版本