最优控制两连杆机械臂

目录

• 问题陈述
• 优化策略
• 运动
• 第一次运动
  • 输入
  • 结果瞬态
• 第二次运动
  • 输入
  • 结果瞬态
• 闭环系统的计算反馈和永久输入
• 讨论

问题陈述

在本博客中，我想将我CodeProject文章简单最优控制软件 [1] 中介绍的技术和软件应用于两连杆机械臂的控制。文章的.NET代码为此问题提供了解决方案。机械臂的数学模型取自Stephen Dodds（导师Dr. Mahboub Baccouch）的著作两连杆机械臂：仿真与控制设计 [2]。预计读者熟悉[1]，因为其中术语、符号和公式在此处被广泛使用。

下面展示了[2]中两连杆垂直定向机械臂的简化模型。

两连杆机械臂简化模型

此处，M_i是集总质量，L_i是连杆长度，Θ_i是连杆的位移角。模型的数学描述由公式(1)给出。

	(1)

该系统本质上是非线性的。为了对其进行最优控制，我们将应用线性二次控制结合拟线性化方法以及[1]中提供的相应软件。

根据[1]中使用的符号，状态向量x对应于(1)中的向量z。系统由两个产生力矩T₁和T₂的电机驱动，这两个电机旋转连杆。为简单起见，假设电机是无惯性的。维度为2的控制向量m对应于力矩。力矩在公式(1)中表示为f_Θ1和f_Θ2。

我们的目标是提出一种控制方案，使系统从初始位置过渡到指定的最终位置并固定在该最终位置。过渡过程应快速。但是，在此过渡期间，角速度和力矩的值应保持在某些合理范围内，以避免损坏系统的机械结构。

对于数值示例，假设质量单位为kg，长度单位为m，时间单位为s，力矩单位为N·m。因此，g = 9.81 m/s²。为了便于阅读，角度单位为度。数值示例采用以下参数

Δt = 0.01, N = 1001。

优化策略

上述目标应形式化。建议的方法是最小化[1]中描述的积分二次成本函数。下面，我们将展示两种优化策略在此系统中的应用。情况1的特点是

• Θ₁和Θ₂角度的期望永久最终值，分别是期望坐标r₀和r₂，
• Θ的永久权重因子为Q₀₀和Q₂₂，以及
• 外部控制参数（力矩）的永久限制，通过单位矩阵Z和零向量u实现。

情况2意味着

• Θ₁和Θ₂角度的可变期望值（分别为r₀和r₂）计算如下

  r_k = 如果 k < s⋅N 则 x_init + (r_final - x_init) / (s⋅N) 否则 r_final     (2)

  其中，k是时间步，s是阈值，s < 1。


• 角度Θ的期望导数永久为零，
• 单位权重矩阵Q，以及
• 力矩不受控制，即矩阵Z = 0。

在这两种情况下，我们都只进行一次迭代，结合恒定的权重矩阵，即可获得恒定的反馈值。

这两种优化策略应用于以下两种运动。

运动

第一次运动

xinit =

$ \begin{bmatrix} 0 \\ 0 \\  0 \\ 0 \end{bmatrix} $

,

xfinal =

$\begin{bmatrix} 45 \\ 0 \\  30 \\ 0 \end{bmatrix}$

和

第二次运动

xinit =

$ \begin{bmatrix} 45 \\ 0 \\  30 \\ 0 \end{bmatrix} $

,

xfinal =

$\begin{bmatrix} 60 \\ 0 \\  -30 \\ 0 \end{bmatrix}$

第一次运动

输入

案例 1

$ Q = \begin{bmatrix} 5000 &0 &0 &0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 5000 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} , Z = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} , r = \begin{bmatrix} 48.5 \\ 0 \\ 32 \\ 0 \end{bmatrix} , u = 0$

案例 2

$ Q = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} , Z = 0 , r = \begin{bmatrix} (2)其中 \hspace{2 mm} s=0.6, r_{final}=48.6\\ 0 \\ (2)其中 \hspace{2 mm} s=0.6, r_{final}=32\\ 0 \end{bmatrix} $

结果瞬态

Θ1

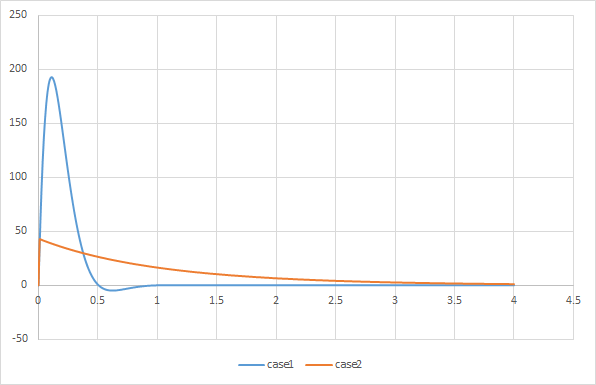dΘ1/dt

T1

Θ2

dΘ2/dt

T2

第二次运动

输入

案例 1

$ Q = \begin{bmatrix} 5000 &0 &0 &0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 5000 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} , Z = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} , r = \begin{bmatrix} 66.5 \\ 0 \\ -19 \\ 0 \end{bmatrix} , u = 0$

案例 2

$ Q = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} , Z = 0 , r = \begin{bmatrix} (2) 其中 \hspace{2 mm} s=0.6, r_{final}=66.5\\ 0 \\ (2) 其中 \hspace{2 mm} s=0.6, r_{final}=-20.5\\ 0 \end{bmatrix} $

结果瞬态

Θ1

dΘ1/dt

T1

Θ2

dΘ2/dt

T2

闭环系统的计算反馈和永久输入

案例 1

反馈  

46.7	7.07	-46.6	-7.06
46.6	7.06	46.6	7.06

第一次运动的输入

13.4

65.5

第二次运动的输入

69.5

38.6

案例 2

反馈

49.9	50.5	-49.8	-50.5
49.7	50.5	49.8	50.5

尽管形式上在情况2下，闭环系统的输入不是恒定的，但计算结果非常接近以下恒定值。

第一次运动的输入

14.4

70.0

第二次运动的输入

75.5

39.9

讨论

两连杆机械臂的最优控制问题并非易事。该系统本质上是非线性的。其解决方案需要通过两个通道（力矩）进行有效的协同控制。如上所示，[1]中提出的最小化积分二次成本函数的技术允许设计人员轻松计算各种控制策略。事实上，我进行了大量计算，使用了期望向量和权重矩阵的各种值，而上述结果只是其中的一小部分。对于讨论的两组输入数据，我们都设法仅通过一次迭代就获得了合理的控制策略，确保了反馈的恒定值。有趣的是，获得的控制策略包括从第二连杆的角度和角速度到第一个执行器的正反馈，这两种控制情况都是如此。由于质量M₁和M₂以及连杆长度L₁和L₂相等，因此两个控制通道具有相似的反馈值。

为了进一步研究，需要检查所提出策略控制的系统在稳定性和对模型不准确性的敏感性。当然，生成更多控制策略（例如，通过多次迭代）总是很有趣的。对于控制的技术实现，提供反馈参数（连杆角度和角速度）的有效测量/估计将是有用的。对于实际系统，应将执行器的动力学包含在被控对象的数学模型中。