三角学 JPEG 处理绘图位图数学转换图形图像 Visual Studio 2010 设计/图形架构师高级中级开发 Visual Studio Windows .NET ASP.NET C#

数字信号处理中的傅里叶变换

Jakub Szymanowski

4.98/5 (59投票s)

2016 年 3 月 7 日

MIT

13分钟阅读

83630

2807

本文介绍了离散傅里叶变换 (DFT 和 FFT 算法) 在数字信号处理中的概念和实现。

引言

频率分析是信号处理中最流行的方法之一。它是信号分解的工具，用于进一步滤波，实际上是从彼此中分离信号分量。

尽管跨越这两个世界（时域和频域）的边界过程可能被视为高级情况，但这样做是值得的，因为另一个世界为我们提供了新的机会并简化了许多问题。

本文介绍了计算离散傅里叶变换各种版本的实现，从傅里叶变换的定义，通过减少计算的算法，直到 Cooley-Tukey 快速傅里叶变换方法。

此外，它还介绍了在信号频谱上执行的最简单操作的重要性及其对时域的影响。

信号

信号可以定义为任何物理值的可变性，它可以表示为单个或多个自变量的函数。在本文中，我们将关注一维时间函数。

在现实世界中，遇到的时间函数位于连续域中。然而，计算机科学的发展导致模拟信号处理变得罕见。在数字世界中创建、实现和测试信号处理算法比设计和开发模拟（电子）设备更具成本效益。

从连续域到离散域

为了获得模拟信号的数字表示，需要将其转换为离散时间域并进行量化。

奈奎斯特-香农采样定理是连续时间信号和离散时间信号之间的联系。该定理也可称为惠特克-奈奎斯特-科捷尔尼科夫-香农采样定理——作者姓氏的选择取决于我们讨论该问题的国家。为了简洁起见，我们将直接称其为采样定理。

采样定理回答了如何采样连续时间信号以获得离散时间信号，并能从中恢复原始（连续时间）信号。根据该陈述，为了获得正确采样的离散时间信号，采样频率必须至少是原始信号中可观察到的最高频率的两倍。

信号分解到频域

这一切始于 1807 年，法国数学家和物理学家约瑟夫·傅里叶引入了三角级数分解（如今称为傅里叶级数方法），以解决金属板上的偏微分热方程。傅里叶的想法是将复杂的周期函数分解为最简单的振荡函数——正弦和余弦的和。

约瑟夫·傅里叶

如果函数f(x)是周期为T的周期函数，并且在区间[x₀, x₀ + T]上是可积的（其积分是有限的），那么它可以转换为级数

$\begin{aligned} f(x) = \frac{a_0}{2} + \sum_{n=1}^{\infty} (a_n \cdot cos(\frac{2 n \pi}{T}x) + b_n \cdot sin(\frac{2 n \pi}{T}x)) \end{aligned}$

其中

$\begin{aligned} a_n = \frac{2}{T} \int_{x_0}^{x_0 + T} f(x) \cdot cos(\frac{2 n \pi}{T}x) dx \\ b_n = \frac{2}{T} \int_{x_0}^{x_0 + T} f(x) \cdot sin(\frac{2 n \pi}{T}x) dx \end{aligned}$

离散傅立叶变换

定义

傅里叶级数可以称为傅里叶变换的先驱，对于数字信号（离散傅里叶变换），它由以下公式描述

$\begin{aligned} X(k) = \frac{1}{N} \sum_{n=0}^{N-1} x(n) \cdot e^{-j \frac{2 \pi}{N} k n } \end{aligned}$

傅里叶变换是可逆的，我们可以通过计算返回到时域

$\begin{aligned} x(n) = \sum_{k=0}^{N-1} X(k) \cdot e^{j \frac{2 \pi}{N} k n } \end{aligned}$

在某些表示法中，我们可以看到除以N被转移到逆计算中——只要我们在正向和反向傅里叶变换中都应用除以N，它就不会干扰计算。

正向和反向离散傅里叶变换的实现如下所示。

/// <summary>
/// Calculates Discrete Fourier Transform of given digital signal x
/// </summary>
/// <param name="x">Signal x samples values</param>
/// <returns>Fourier Transform of signal x</returns>
public Complex[] DFT(Double[] x)
{
    int N = x.Length; // Number of samples
    Complex[] X = new Complex[N];

    for (int k = 0; k < N; k++)
    {
        X[k] = 0;

        for (int n = 0; n < N; n++)
        {
            X[k] += x[n] * Complex.Exp(-Complex.ImaginaryOne * 2 * Math.PI * (k * n) / Convert.ToDouble(N));
        }

        X[k] = X[k] / N;

    }

    return X;
}



/// <summary>
/// Calculates inverse Discrete Fourier Transform of given spectrum X
/// </summary>
/// <param name="X">Spectrum complex values</param>
/// <returns>Signal samples in time domain</returns>
public Double[] iDFT(Complex[] X)
{
    int N = X.Length; // Number of spectrum elements
    Double[] x = new Double[N];

    for (int n = 0; n < N; n++)
    {
        Complex sum = 0;

        for (int k = 0; k < N; k++)
        {
            sum += X[k] * Complex.Exp(Complex.ImaginaryOne * 2 * Math.PI * (k * n) / Convert.ToDouble(N));
        }

        x[n] = sum.Real; // As a result we expect only real values (if our calculations are correct imaginary values should be equal or close to zero)
    }

    return x;
}

在反向傅里叶变换的代码实现中，常常会犯一个错误，即通过其幅值将复数值转换为实数——在这种情况下，我们将得到|x(n)|而不是x(n)。

离散傅里叶变换的实际计算示例（按定义）

为了验证算法，让我们创建一个由两个正弦波之和组成的信号

$\begin{aligned} x_1(n) = sin(0.02 \pi n) \end{aligned}$

$\begin{aligned} x_2(n) = 0.25 \cdot sin(0.2 \pi n) \end{aligned}$

我们将x₁(n)表示为原始信号，将x₂(n)表示为干扰信号（噪声）。这两个信号的和x(n) = x₁(n)+x₂(n)在这种情况下是干扰信号。

$\begin{aligned} x(n) = x_1(n) + x_2(n) \end{aligned}$

$\begin{aligned} n = 0, 1, ..., 100 \end{aligned}$

图 1. 原始信号和干扰信号

图 2. 信号之和（干扰信号）

由于我们将信号创建为两个正弦波之和，因此根据傅里叶定理，我们应该在其频率图像中看到集中在两个频率f₁和f₂以及它们的负值-f₁和-f₂。

图 3. 干扰信号的幅度谱。

如果傅里叶定理正确，那么通过从频谱中去除由干扰信号产生的条带，我们应该能够得到原始信号。

图 4. 去除干扰频率后的频谱及反向 DFT 结果

正如我们在图 4 中观察到的，我们的输出信号接近原始信号，失真是由数值运算产生的额外条带引起的。让我们将它们全部移除，只保留两个主要条带。

图 5. 仅包含主频率的频谱及其反向 DFT 结果。

图 5 中的输出信号看起来像完美的正弦波。但要查看输出信号与原始信号之间的细微差别，请参见下面的比较。

图 6. 原始信号与输出信号比较。

在图 3 中我们看不到任何负值，那么为什么我们说计算出的频谱集中在两个频率f₁和f₂以及它们的负值-f₁和-f₂周围呢？

这是因为我们习惯于分析定义在对称于原点的范围内的信号。如果我们记我们受干扰的信号x(n)为

$\begin{aligned} x(n) = x_1(n) + x_2(n) \end{aligned}$

$\begin{aligned} n = -50, -49, ..., -1, 0, 1, ..., 49, 50 \end{aligned}$

图 7. 移位信号

并在我们的算法中进行微小改动

/// <summary>
/// Calculates forward Discrete Fourier Transform of given digital signal x with respect to sample numbers
/// </summary>
/// <param name="x">Signal x samples values</param>
/// <param name="SamplesNumbers">Samples numbers vector</param>
/// <returns>Fourier Transform of signal x</returns>
public Complex[] DFT(Double[] x, int[] SamplesNumbers)
{
    int N = x.Length; // Number of samples
    Complex[] X = new Complex[N];

    for (int k = 0; k < N; k++)
    {
        X[k] = 0;

        Double s1 = SamplesNumbers[k]; // Get sample index

        for (int n = 0; n < N; n++)
        {
            Double s2 = SamplesNumbers[n]; // Get sample index
            X[k] += x[n] * Complex.Exp(-Complex.ImaginaryOne * 2 * Math.PI * (s1 * s2) / Convert.ToDouble(N));
        }

        X[k] = X[k] / N;
    }
    return X;
}

我们将得到如下所示的幅度谱。

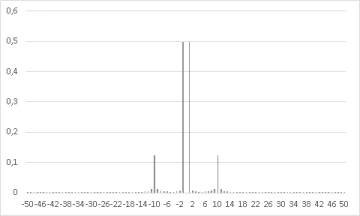
图 8. 移位信号的幅度谱

反向 DFT 方法也需要进行相同的更改。

/// <summary>
/// Calculates inverse Discrete Fourier Transform of given spectrum X with respect to sample numbers
/// </summary>
/// <param name="X">Spectrum complex values</param>
/// <param name="SamplesNumbers">Samples numbers vector</param>
/// <returns>Signal samples in time domain</returns>
public Double[] iDFT(Complex[] X, int[] SamplesNumbers)
{
    int N = X.Length; // Number of spectrum elements
    Double[] x = new Double[N];

    for (int n = 0; n < N; n++)
    {
        Complex sum = 0;
        Double s1 = SamplesNumbers[n]; // Get sample index

        for (int k = 0; k < N; k++)
        {
            Double s2 = SamplesNumbers[k];  // Get sample index
            sum += X[k] * Complex.Exp(Complex.ImaginaryOne * 2 * Math.PI * (s1 * s2) / Convert.ToDouble(N));
        }

        x[n] = sum.Real; // As a result we expect only real values (if our calculations are correct imaginary values should be equal or close to zero)
    }

    return x;
}

请注意，通过将信号移位到相对于原点对称的位置，我们计算出了移位后的频谱

$\begin{aligned} X(k) \rightarrow X(k - \frac{N}{2}) \end{aligned}$

如果通过以下公式更改原始信号，也可以实现相同效果

$\begin{aligned} x(n) \rightarrow (-1)^n \cdot x(n) \end{aligned}$

在这种情况下，无需存储实际的样本数量。使用此方法如下所示。

/// <summary>
/// Shifts spectrum by changing original signal before Fourier Transform
/// </summary>
/// <param name="x">Original signal</param>
/// <returns>Shifted signal</returns>
public Double[] Shift(Double[] x)
{
    int N = x.Length;

    for (int i = 0; i < N; i++)
    {
        x[i] = (int)Math.Pow(-1, i) * x[i];
    }

    return x;
}

计算量减少的离散傅里叶变换

让我们再次查看正向离散傅里叶变换的定义

$\begin{aligned} X(k) = \frac{1}{N} \sum_{n=0}^{N-1} x(n) \cdot e^{-j \frac{2 \pi}{N} k n } \end{aligned}$

将辅助变量记为W_N

$\begin{aligned} W_N = e^{-j \frac{2 \pi }{N}}\end{aligned}$

那么我们的公式将变为

$\begin{aligned} X(k) = \frac{1}{N} \sum_{n=0}^{N-1} x(n) \cdot W_N ^{k n} \end{aligned}$

我们还可以注意到，如果k = 0或n = 0，我们会得到

$\begin{aligned} W_N^{k n} = 1 \end{aligned}$

因此，DFT 的表示形式可以写成矩阵形式

$\begin{aligned} \begin{bmatrix} X[0] \\ X[1] \\ \vdots \\ X[N-1] \end{bmatrix} = \frac{1}{N} \begin{bmatrix} 1 & 1 & 1 & \dots & 1 \\ 1 & W_N & W_N^2 & \dots & W_N^{N-1} \\ 1 & W_N^2 & W_N^4 & \dots & W_N^{N-2} \\ 1 & W_N^3 & W_N^6 & \dots & W_N^{N-3} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & W_N^{N-1} & W_N^{N-2} & \dots & W_N \end{bmatrix} \cdot \begin{bmatrix} x[0] \\ x[1] \\ \vdots \\ x[N-1] \end{bmatrix} \end{aligned}$

由此可见，为了确定N个样本信号的离散傅里叶变换，我们必须执行N²次乘法运算，并确定矩阵W_N中的（N-1）²个系数。请记住，乘法运算是处理器上最耗时的运算之一。

让我们回到因子W_N，并考虑N = 4个样本信号x(n)。为了计算 X(k)，我们需要找到矩阵系数的值

$\begin{aligned} \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & W_4 & W_4^2 & W_4^3 \\ 1 & W_4^2 & W_4^4 & W_4^2 \\ 1 & W_4^3 & W_4^2 & W_4 \end{bmatrix} \end{aligned}$

我们有

$\begin{aligned} W_4 = e^{-j \frac{\pi}{2}} = cos(-\frac{\pi}{2}) + j \cdot sin(-\frac{\pi}{2}) = cos(\frac{\pi}{2}) - j \cdot sin(\frac{\pi}{2}) = -j \end{aligned}$

其中

$\begin{aligned} e^{j \phi} = cos(\phi) + j \cdot sin(\phi) \end{aligned}$

是欧拉公式。

接下来的值是

$\begin{aligned} \begin{matrix} W_4^2 = -1 \\ W_4^3 = j \\ W_4^4 = -1 \end{matrix} \end{aligned}$

注意到

$\begin{aligned} \begin{matrix} W_4^2 = -W_4^0 \\ W_4^3 = -W_4^1 \end{matrix} \end{aligned}$

对于N=8也可以注意到类似的情况

$\begin{aligned} \begin{matrix} W_8^1 = e^{-j \frac{\pi}{4}} = cos(\frac{\pi}{4}) - j \cdot sin(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}(1 - j) = \frac{1-j}{\sqrt{2}} \\ W_8^2 = (\frac{(1-j)^2}{2}) = -j \\ W_8^3 = -j \cdot \frac{1-j}{\sqrt{2}} = \frac{-1-j}{\sqrt{2}} \\ W_8^4 = \frac{-1-j}{\sqrt{2}} \cdot \frac{1-j}{\sqrt{2}} = -1 \\ W_8^5 = - \frac{1-j}{\sqrt{2}} \\ W_8^6 = - (\frac{1-j}{\sqrt{2}})^2 = j \\ W_8^7 = j \cdot \frac{1-j}{\sqrt{2}} = \frac{1+j}{\sqrt{2}} \\ W_8^8 = \frac{1+j}{\sqrt{2}} \cdot \frac{1-j}{\sqrt{2}} = 1 \end{matrix} \end{aligned}$

这导致

$\begin{aligned} \begin{matrix} W_8^4 = -W_8^0 \\ W_8^5 = -W_8^1 \\ W_8^6 = -W_8^2 \\ W_8^7 = -W_8^3 \end{matrix} \end{aligned}$

总的来说，对于N个样本信号，我们可以写成

$\begin{aligned} \begin{matrix} W_N^z = - W_N^{z - \frac{N}{2}} \\ z = \frac{N}{2}, \frac{N}{2} + 1, \frac{N}{2} + 2, ..., N \end{matrix}\end{aligned}$

这个观察使我们得出结论，在确定 DFT 时，我们只计算N/2 - 1个频谱系数，而其他系数可以从前面的系数获得——这是频谱对称性的性质。由于这个观察，算法内的运算次数减少了四倍。只有当我们处理物理信号（即实值信号）时，这个观察才成立。

/// <summary>
/// Calculates forward Discrete Fourier Transform of given digital signal x with reduced number of multiplications
/// </summary>
/// <param name="x">Signal x samples values</param>
/// <returns>Fourier Transform of signal x</returns>
public Complex[] DFT2(Double[] x)
{
    int N = x.Length; // Number of samples
    Complex[] X = new Complex[N];

    // Zero-index element calculation
    X[0] = x.Sum() / N;

    for (int k = 1; k < N/2 + 1; k++)
    {
        X[k] = 0;

        for (int n = 0; n < N; n++)
        {
            X[k] += x[n] * Complex.Exp(-Complex.ImaginaryOne * 2 * Math.PI * (k * n) / Convert.ToDouble(N));
        }

        X[k] = X[k] / N;

        // Miss additional calculation for center element
        if (k != N / 2)
        {
            X[N - k] = new Complex(X[k].Real, -X[k].Imaginary);
        }
    }

    return X;
}

/// <summary>
/// Calculates forward Discrete Fourier Transform of given digital signal x with respect to sample numbers and reduced number of multiplications
/// </summary>
/// <param name="x">Signal x samples values</param>
/// <param name="SamplesNumbers">Samples numbers vector</param>
/// <returns>Fourier Transform of signal x</returns>
public Complex[] DFT2(Double[] x, int[] SamplesNumbers)
{
    int N = x.Length; // Number of samples
    Complex[] X = new Complex[N];

    for (int k = 0; k < N / 2 + 1; k++)
    {
        X[k] = 0;
        Double s1 = SamplesNumbers[k];

        for (int n = 0; n < N; n++)
        {
            Double s2 = SamplesNumbers[n];
            X[k] += x[n] * Complex.Exp(-Complex.ImaginaryOne * 2 * Math.PI * (s1 * s2) / Convert.ToDouble(N));
        }

        X[k] = X[k] / N;

        // Miss additional calculation for center element
        if (k != N/2)
        {
            X[N - k - 1] = new Complex(X[k].Real, -X[k].Imaginary);
        }
    }

    return X;
}

示例

图 9. 图 2 中信号的幅度谱。使用计算量减少的 DFT 计算

图 10. 图 7 中信号的幅度谱。使用计算量减少的 DFT 计算

快速傅里叶变换

傅里叶变换公式可以分解为

$\begin{aligned} X(k) = \frac{1}{N} \sum_{n=0}^{N-1} x(n) \cdot e^{-j \frac{2 \pi}{N} k n } = \frac{1}{N} \sum_{n=0}^{\frac{N}{2}-1} x(2n) \cdot W_N^{2nk} + \frac{1}{N} \sum_{n=0}^{\frac{N}{2}-1} x(2n + 1) \cdot W_N^{(2n+1)k} \end{aligned}$

其中

$\begin{aligned} W_N^{2nk} = e^{-j \frac{2 \pi}{N} 2 n k} = e^{-j \frac{2 \pi}{\frac{N}{2}}nk} = W_{\frac{N}{2}}^{n k} \end{aligned}$

和

$\begin{aligned} W_N^{(2n+1)k} = W_N^{2nk + k} = W_N^{2nk} \cdot W_N^{k} = W_{\frac{N}{2}}^{n k} \cdot W_N^{k} \end{aligned}$

因此

$\begin{aligned} X(k) = \frac{1}{N} \sum_{n=0}^{\frac{N}{2}-1} x(2n) \cdot W_{\frac{N}{2}}^{n k} + \frac{1}{N} \cdot W_N^{k} \sum_{n=0}^{\frac{N}{2}-1} x(2n + 1) \cdot W_{\frac{N}{2}}^{n k} \end{aligned}$

这可以写成一个更简单的形式，将对偶数样本的计算与对奇数样本的计算分开

$\begin{aligned} X(k) = X_E(k) + W_N^k \cdot X_O(k) \end{aligned}$

因此，参照我们之前对N = 8情况的计算，可以写成

$\begin{aligned} \begin{matrix} X(0) = X_E(0) + W_8^0 \cdot X_O(0) \\ X(1) = X_E(1) + W_8^1 \cdot X_O(1) \\ X(2) = X_E(2) + W_8^2 \cdot X_O(2) \\ X(3) = X_E(3) + W_8^3 \cdot X_O(3) \\ X(4) = X_E(0) + W_8^4 \cdot X_O(0) = X_E(0) - W_8^0 \cdot X_O(0) \\ X(5) = X_E(1) + W_8^5 \cdot X_O(1) = X_E(1) - W_8^1 \cdot X_O(1) \\ X(6) = X_E(2) + W_8^6 \cdot X_O(2) = X_E(2) - W_8^2 \cdot X_O(2) \\ X(7) = X_E(3) + W_8^7 \cdot X_O(3) = X_E(3) - W_8^3 \cdot X_O(3) \\ \end{matrix} \end{aligned}$

这可以用图表示

图 11. DFT 分解为偶数和奇数样本计算。

请注意，元素：

和

可以以相同的方式计算：x(0)、x(4)、x(1) 和x(5) 在它们的图表中是偶数索引，而x(2)、x(6)、x(3) 和x(7) 是奇数索引。将它们组合成有序对，上面的图可以重绘

最后，在本例中

图 12. 快速傅里叶变换（RADIX-2）用于N = 8信号。

为了表示N = 8信号的 DFT 定义，我们不得不执行 64 次乘法运算，但由于上述观察，我们只执行了 12 次。信号中的样本数量越多，使用 FFT 算法在计算数量上带来的好处就越大，因为对于N个样本信号的计算量可以确定为

$\begin{aligned} \begin{matrix} \frac{N}{2} log_2(N) \end{matrix} \end{aligned}$

这种计算的基本元素称为“蝶形”（butterfly）

其中

$\begin{aligned} \begin{matrix} Y(k) = y(k) + W_N^k \cdot y(k + \frac{N}{2}) \\ Y(k + \frac{N}{2}) = y(k) - W_N^k \cdot y(k + \frac{N}{2}) \end{matrix} \end{aligned}$

只能假设N是2的幂，才能对较小的基本“蝶形”进行连续分解。

快速傅里叶变换的实践

适当数量的样本

处理信号的最简单方法是使其样本数量是2的幂，只需用零填充缺失的样本。根据信号结构，可以从右侧、左侧或两侧添加。

图 13. 图 2 中补充的信号

排序样本

为了将连续的信号样本连接成相应的对，我们使用了预排序算法。然而，FFT 算法可以在未排序的样本上执行，并且排序操作（以相同的方式）可以在频谱的样本上执行。

在硬件频谱分析仪和低级编程语言中，排序样本要容易得多，因为该操作基于索引样本的二进制表示中的位进行简单反转。

在我们的N = 8信号中，我们可以注意到

$\begin{aligned} \begin{matrix} x(0) & 000 & \rightarrow & 000 & x(0) \\ x(1) & 001 & \rightarrow & 100 & x(4) \\ x(2) & 010 & \rightarrow & 010 & x(2) \\ x(3) & 011 & \rightarrow & 110 & x(6) \\ x(4) & 100 & \rightarrow & 001 & x(1) \\ x(5) & 101 & \rightarrow & 101 & x(5) \\ x(6) & 110 & \rightarrow & 011 & x(3) \\ x(7) & 111 & \rightarrow & 111 & x(7) \end{matrix} \end{aligned}$

一般情况下的方法实现

/// <summary>
/// Input data sorting using bit reversal method
/// </summary>
/// <param name="x">Original input signal samples</param>
/// <returns>Sorted signal samples</returns>
public Double[] FFTDataSort(Double[] x)
{
    int N = x.Length; // signal length

    if (Math.Log(N, 2) % 1 != 0)
    {
        throw new Exception("Number of samples in signal must be power of 2");
    }

    Double[] y = new Double[N]; // output (sorted) vector

    int BitsCount = (int)Math.Log(N, 2); // maximum number of bits in index binary representation
    
    for (int n = 0; n < N; n++)
    {
        string bin = Convert.ToString(n, 2).PadLeft(BitsCount, '0'); // index binary representation
        StringBuilder reflection = new StringBuilder(new string('0', bin.Length));

        for (int i = 0; i < bin.Length; i++)
        {
            reflection[bin.Length - i - 1] = bin[i]; // binary reflection
        }

        int number = Convert.ToInt32(reflection.ToString(),2); // new index

        y[number] = x[n];

    }

    return y;

}

然而，该操作可以执行得更快，无需将索引号转换为二进制形式

/// <summary>
/// Input data sorting using index shift method
/// </summary>
/// <param name="x">Original input signal samples</param>
/// <returns>Sorted signal samples</returns>
public Double[] FFTDataSort2(Double[] x)
{
    int N = x.Length; // signal length

    if (Math.Log(N, 2) % 1 != 0)
    {
        throw new Exception("Number of samples in signal must be power of 2");
    }

    int m = 1; // original index
    
    for (int n = 0; n < N - 1; n++) // n - new index
    {
        if (n < m)
        {
            Double T = x[m-1];
            x[m-1] = x[n];
            x[n] = T;
        }

        int s = N / 2; // shift operator

        while (s < m)
        {
            m = m - s;
            s = s / 2;
        }

        m = m + s;
    }

    return x;

}

图 14. 排序后的信号样本（图 2 的信号，在右侧补充）

快速傅里叶变换算法

FFT 算法的实现如下所示。

/// <summary>
/// Calculates forward Fast Fourier Transform of given digital signal x
/// </summary>
/// <param name="x">Signal x samples values</param>
/// <returns>Fourier Transform of signal x</returns>
public Complex[] FFT(Double[] x)
{
    int N = x.Length; // Number of samples

    if (Math.Log(N, 2) % 1 != 0)
    {
        throw new Exception("Number of samples in signal must be power of 2");
    }


    Complex[] X = new Complex[N]; // Signal specturm

    // Rewrite real signal values to calculated spectrum
    for (int i = 0; i < N; i++)
    {
        X[i] = new Complex(x[i], 0);
    }

    int S = (int)Math.Log(N, 2); // Number of calculation stages

    for (int s = 1; s < S + 1; s++) // s - stage number
    {
        int BW = (int)Math.Pow(2, s - 1); // the width of butterfly
        int Blocks = (int)(Convert.ToDouble(N) / Math.Pow(2, s)); // Number of blocks in stage
        int BFlyBlocks = (int)Math.Pow(2, s - 1); // Number of butterflies in block
        int BlocksDist = (int)Math.Pow(2, s); // Distnace between blocks

        Complex W = Complex.Exp(-Complex.ImaginaryOne * 2 * Math.PI / Math.Pow(2, s)); // Fourier Transform kernel

        for (int b = 1; b < Blocks + 1; b++)
        {
            for (int m = 1; m < BFlyBlocks + 1; m++)
            {
                int itop = (b - 1) * BlocksDist + m; // top butterfly index
                int ibottom = itop + BW; // bottom butterfly index

                Complex Xtop = X[itop-1]; // top element -> X(k)
                Complex Xbottom = X[ibottom-1] * Complex.Pow(W, m - 1); // bottom element -> X(k + N/2)

                // Butterfly final calculation
                X[itop-1] = Xtop + Xbottom;
                X[ibottom-1] = Xtop - Xbottom;
            }
        }
    }

    // Spectrum scaling
    for (int i = 0; i < N; i++)
    {
        X[i] = X[i] / Convert.ToDouble(N);
    }

    return X;
}

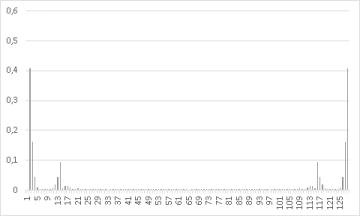
图 15. FFT - 排序样本信号的幅度谱（来自图 14）

图 16. FFT - 移位信号（来自图 14）的幅度谱，已排序样本

通过对前向 FFT 方法进行微小更改，可以实现反向快速傅里叶变换

/// <summary>
/// Calculates inverse Fast Fourier Transform of given spectrum
/// </summary>
/// <param name="X">Spectrum values</param>
/// <returns>Signal samples</returns>
public Double[] iFFT(Complex[] X)
{
    int N = X.Length; // Number of samples
    Double[] x = new Double[N];
    int E = (int)Math.Log(N, 2);

    for (int e = 1; e < E + 1; e++)
    {
        int SM = (int)Math.Pow(2, e - 1);
        int LB = (int)(Convert.ToDouble(N) / Math.Pow(2, e));
        int LMB = (int)Math.Pow(2, e - 1);
        int OMB = (int)Math.Pow(2, e);

        Complex W = Complex.Exp(Complex.ImaginaryOne * 2 * Math.PI / Math.Pow(2, e)); // changed sign - our minor change

        for (int b = 1; b < LB + 1; b++)
        {
            for (int m = 1; m < LMB + 1; m++)
            {
                int g = (b - 1) * OMB + m;
                int d = g + SM;

                Complex xgora = X[g - 1];
                Complex xdol = X[d - 1] * Complex.Pow(W, m - 1);

                X[g - 1] = xgora + xdol;
                X[d - 1] = xgora - xdol;
            }
        }
    }

    for (int i = 0; i < N; i++)
    {
        x[i] = X[i].Real;
    }

    return x;
}

图 17. 使用反向快速傅里叶变换从图 15 的频谱恢复的信号。

正如所注意到的，用额外零样本补充的信号对频谱有影响——在图 15 和 16 中可以看到额外的条带。尽管如此，只要我们保留它们以进行进一步计算，我们就能恢复原始信号。

然而，让我们看看是否仍然可以通过 FFT 方法将信号与噪声分离并恢复。

首先，去除疑似干扰的条带

图 18. 滤波后的信号频谱

其次，计算反向 FFT

图 19. 反向 FFT - 恢复的信号

第三，裁剪额外的样本

图 20. 没有额外样本的信号。

最后，比较原始（未受干扰）信号与我们的滤波结果。

图 21. 原始信号与输出信号比较（快速傅里叶变换）。

使用代码

本文介绍的所有信号处理算法均在附带的源代码中实现。要开始使用 DiscreteFourierTransform 库，只需声明其命名空间

using DiscreteFourierTransform;

创建新对象

DiscreteFourierTransform.DiscreteFourierTransform dft = new DiscreteFourierTransform.DiscreteFourierTransform();

并开始您在频域中的数字信号处理之旅。

库方法和应用程序

测试信号

DLL 中包含干扰的正弦信号和样本索引

Double[] signal = dft.testsignal();
int[] n = dft.testsignalindexes();

离散傅立叶变换

// --- Discrete Fourier Transform by definition

Complex[] X = dft.DFT(signal); // discrete fourier transform by definition

Double[] A = dft.Amplitude(X); // amplitude spectrum from X

Complex[] Xa = dft.DFT(signal, n); //discrete fourier transform by definition with samples numbers

Double[] signal2 = dft.Shift(signal); // Signal shift method

Complex[] Xb = dft.DFT(signal2); // discrete fourier transform by definition of shifted signal

// Compare Xa and Xb and see if we were correct!

反向离散傅里叶变换

// --- Inverse Discrete Fourier Transform by definition

Double[] x = dft.iDFT(X); // inverse discrete fourier transform by definition

Double[] xa = dft.iDFT(Xa, n); // inverse discrete fourier transform by definition (with samples numbers)

Double[] xb = dft.iDFT(Xb); // inverse discrete fourier transform by definition of shifted signal

// Compare x, xa and xb. Any other operation needs to be performed at xb to restore original?

计算量减少的离散傅里叶变换

// --- Discrete Fourier Transform with reduced number of calculation

Complex[] X2 = dft.DFT2(signal); // discrete fourier transform with reduced number of calculation

Complex[] X2a = dft.DFT2(signal, n); // discrete fourier transform with reduced number of calculation with samples numbers

Complex[] X2b = dft.DFT2(dft.Shift(signal), n); // discrete fourier transform with reduced number of calculation (shifted signal)

快速傅里叶变换

带零的信号打包

// Signal pack with zeros

Double[] signalpack = dft.SignalPackRight(signal); // Complement at right to N = nearest power of 2

Double[] signalpack2 = dft.SignalPackLeft(signal); // Complement at left to N = nearest power of 2

Double[] signalpack3 = dft.SignalPackBoth(signal); // Complement at both sides to N = nearest power of 2

样本排序

// Samples sorting

Double[] signal3 = dft.FFTDataSort(signalpack); // using bit reverse

Double[] signal4 = dft.FFTDataSort2(signalpack); // using shift method

// Compare signal3 and signal4 - should be equal!

快速傅里叶变换

Complex[] X3 = dft.FFT(signal3); // fast fourier transform

Complex[] X3a = dft.FFT(dft.Shift(signal3)); // shifted spectrum - fast fourier transform

反向快速傅里叶变换

频谱条带排序

Complex[] X3s = dft.FFTDataSort(X3); // spectrum sort using bit reverse

Complex[] X3as = dft.FFTDataSort2(X3); // spectrum sort using shift method

反向快速傅里叶变换

Double[] x3 = dft.iFFT(X3s); // inverse fast fourier transform

// ----------------- Compare x3 with signal!!! ---------------