	Marin Mersenne 1588-1648 梅森数定义：梅森数的形式为 M_n = 2ⁿ – 1，其中 n 是正整数。梅森素数定义：梅森素数的形式为 M_p = 2^p - 1，其中 p 和 2^p - 1 都是素数。
	Pierre de Fermat 1601-1665 费马数定义：费马数的形式为 F_n = 2^{2^n}+1，其中 n 是正整数。费马小定理。设 p 为素数，且 p \| b。则 b^p^-1 º 1 (mod p)
	Leonhard Euler 1707-1783 欧拉伪素数定义：以 2 为底的欧拉伪素数的形式为 E_n = 1 mod n，并且是以 2 为底的最小正指数 cn+1 的最大数，其中 c 是正整数，n 是最小正指数。所有因子都为此形式。（参见 Germain）欧拉-费马定理。*若 gcd(b, n) = 1，则 b^f(n) º 1(mod n)。
	Sophie Germain 1776-1831 热尔曼伪素数定义：热尔曼数 G_n = cn+1，其中 c 是正整数，n 是以 2 为底的最小正指数。若 n 为奇数或 n = 2^x，则 G_n* = 2kn+1 或 c = 2k。若 n 为偶数，除了 n = 2^x，则 G_n* = c * n + 1。所有因子都为此形式。
	Francois Lucas 1842-1891 费马-卢卡斯数定义：费马-卢卡斯数的形式为 FL_n = 2ⁿ+1，其中 n 是正整数。阶（ord）定义：设 gcd(b, n) = 1。使 b^mº 1(mod n) 的最小正整数 m 称为 b 模 n 的阶，记为 ord_nb。

我们中的许多人在高中和大学时期都熟悉这些古典数论学家及其公式。本文将通过公式化来阐述他们的公式之间的关系以及它们的欧拉伪素数属性。例如，M_p = E_p（见下方的图 1），它有一个素数基底，但具有不同的素数基底，从而产生 (p-1) ... 0 的二进制序列。类似地，F_n = 2^{2^n}+1 等同于欧拉伪素数类，其中 J = 2*2ⁿ 或 2ⁿ⁺¹，则 E_j = F_n 有一个素数基底为 2，并产生一个位 n + 位 0 的二进制序列，其中位 n 是 2ⁿ⁺¹ 的乘法函数。这也适用于其他素数基底。例如，E₉ = 73 有一个素数基底为 3，在计算环境中具有两个置位位 {1, 0}。然而，在数学环境中，这两个位是 {2, 1}。当乘以 3 时，因为 9 = 3²，序列变为位 {6, 3} + 位 0。此方法也适用于多个素数基底。例如，E₁₅ = 151 有两个素数基底，3 和 5，素数基底序列交织在以下序列模式中。序列的起始是 15 = 3 * 5，3 + 5 = 8，所以第一个置位位是 15 – 8 = 7，然后 7 – 3 = 4，然后 4 – 3 = 1，然后 7 – 5 = 2。序列变为位 {7, 4, 1, 2} + 位 0。注意：E_2n = FL_n

图 1

图 2 显示了上述过程的结果，使用一个和两个素数基底，以及每个基底的指数为一。它还显示了梅森数在简化为欧拉伪素数时的关系。图 3 和图 4 显示的数据与第一个图类似，指数大于或等于一，并显示了其他基底的费马数并简化为欧拉伪素数。图 5 显示了费马-卢卡斯数，这是一个比费马数更大的类，以及它们如何被简化为欧拉伪素数。在所有这些图中，黑色集合字符是二进制序列，彩色字符是整数结果。

图 2

图 3

图 4

图 5

下面的代码生成上述图表中具有一个和两个基底序列的信息，指数可达计算机资源允许的范围。

private static BigInteger NonOrderedSeq(long p1, long p2, long multiplier)
{
    long h, n;
    BigInteger result = new BigInteger(0);
    BigInteger temp1 = new BigInteger(0);
    BigInteger temp2 = new BigInteger(0);
 
    if (p1 == 1)
        h = p2;
    else
        h = (p1 - 1) * p2;
 
    while (h > 0)
    {
        n = h;
        while (n >= p1)
        {
            n = n - p1;
            if (p1 == 1)
                result = result + BigInteger.setBit(n * multiplier);
            else
                temp1 = temp1 + BigInteger.setBit(n * multiplier);
        }
 
        h = h - p2;
    }
 
    if (result == 0)
        if (multiplier == 1)
            result = temp1 + BigInteger.setBit(0);
        else
        {
            temp2 = temp1 << Convert.ToInt32(multiplier);
            result = temp2 - temp1;
            result = result + BigInteger.setBit(0);
        }
    return result;
}

在上面的图 5 中，您可能已经注意到，在某些双基底的情况下，序列尚未完全简化为欧拉伪素数。例如，E₆ = 1 但显示为 3，E₂₀ = 41 但显示为 205。所有大于 1 的基底都有一个阶因子。下面的图 6 是这些因子的小集合。因子确定如下：

Order_factor22 = Number/Factor2^e 然后用 Factor2 除以序列
Order_factor32 = Number/Factor3^e 然后用 Factor3 除以序列
Order_factor42 = Number/Factor4^e 然后用 Factor4 除以序列
等等

图 6

下面的图 7 提供了确定欧拉伪素数的通用公式，该公式根据素数基底的数量进行计算。

图 7

下面的图 8 和图 9 显示了通用公式如何应用于具体情况。

图 8

图 9

请注意，在上面的图 9 的二进制序列中，除法前的乘法结果会非常大。这会在有限的计算环境中缩小探索范围，并随着 E 的 n 增加而减慢结果。下面的图 10 显示了如何通过除法来实现这一点。下面的图 11 显示了除法分组如何分解为帕斯卡三角形。下面的图 12 显示了除法从三角形的基部移动到顶点的帕斯卡三角形，这相当于通过矩阵进行乘法和除法。然而，对于上面的图 9 中的 A₇，计算被限制在最大位 24023。

下面的代码创建了用于除法的帕斯卡三角形。

        private static object[,] PyramidPairing(long numOfBases)
        {
            long j, k;
            object[,] elements = new object[numOfBases, numOfBases];
            for (j = 0; j <= numOfBases-1; j++)
            {
                if (j == 0)
                    elements[j, j] = 1;
                else
                    for (k = 0; k <= j; k++)
                    {
                        if (k == 0)
                            elements[j,k] = elements[j-1,k];
                        if (k > 0 && k < j)
                            elements[j,k] = Convert.ToInt64(elements[j-1,k-1]) + 
                                            Convert.ToInt64(elements[j-1,k]);
                        if (k == j)
                            elements[j,k] = elements[j-1,k-1];
                    }
            }
            return elements;
        }

图 10

图 11

图 12

欧拉伪素数代码片段

安装

        public static BigInteger Euler(object[,] ArrIn)
        {
            #region Euler setup
 
            object[,] Arr1;
            object[,] Arr2;
            object[,] element;
            BigInteger[] division;
            BigInteger number = new BigInteger(1);
            long i, j, k, nGroup, numDiv, iCount;
            long p1, p2;
 
            Arr1 = ArrIn;
           
            if (Arr1.GetUpperBound(0) < 1)
            {
                p1 = 1;
                p2 = Convert.ToInt32(Arr1[0, 0]);
            }
            else
            {
                p1 = Convert.ToInt32(Arr1[0, 0]);
                p2 = Convert.ToInt32(Arr1[1, 0]);
            }

            #endregion Euler setup

BaseA 序列

            #region BaseA Sequence

            ///
            /// Creates the matrixed sequences
            /// If one or two base sequence then
            /// division[i] with i = 0 contains the result.
            ///
            Arr2 = AExp(Arr1);
            division = new BigInteger[Arr2.GetUpperBound(0) + 1];
            for (i = 0; i <= Arr2.GetUpperBound(0); i++)
                division[i] = new BigInteger(Number_Theory.NumberTheory.baseA2(p1.ToString(), 
                              p2.ToString(), Convert.ToInt64(Arr2[Arr2.GetUpperBound(0)-i, 0])));
 
            #endregion BaseA Sequence

大于 2 的素数基底

            #region Prime Base Greater Than 2

            //  Prime bases greater than 2

            if (Arr1.GetUpperBound(0) > 1)
            {
                element = PyramidPairing(Arr1.GetUpperBound(0) - 1);
                numDiv = Convert.ToInt64(BigInteger.Power(new BigInteger(2), 
                         Arr1.GetUpperBound(0) - 1).ToString());
                Boolean[] bDivides = new Boolean[numDiv/2];
                //division = new BigInteger[numDiv];
                numDiv = numDiv - 1;
 
                ///
                /// Divides up the pyramid from the base to the apex
                /// with Division[i] where i = 0 is the apex.
                ///
                for (i = element.GetUpperBound(0); i >= 0; i--)
                {
                    iCount = 0;
                    numDiv = 0;
                    bDivides = new Boolean[division.GetLength(0) / 2];
                    BigInteger[] hold = new BigInteger[division.GetLength(0) / 2];
                    for (j = 0; j <= i; j++)
                    {
                        nGroup = Convert.ToInt64(element[i, j]);
                        for (k = 0; k <= nGroup - 1; k++)
                        {
                            bDivides[iCount] = false;
                            if (division[numDiv] % division[numDiv + nGroup] == 0)
                                bDivides[iCount] = true;
 
                            hold[iCount] = division[numDiv] / division[numDiv + nGroup];
                            numDiv = numDiv + 1;
                            iCount = iCount + 1;
                        }
                        numDiv = numDiv + nGroup;
                    }
                    division = new BigInteger[hold.GetLength(0)];
                    for (j = 0; j <= hold.GetUpperBound(0); j++)
                        division[j] = hold[j];
                }
            }
 
            #endregion Prime Base Greater Than 2

阶基底因子？

            #region Order Base Factor?
            ///
            /// Checks for the order base factor
            /// for bases greater than one and
            /// reduces the result if factor exists.
            ///
            if (Arr1.GetUpperBound(0) > 0)
            {
                for (j = 0; j <= Arr1.GetUpperBound(0); j++)
                    number = number * BigInteger.Power(new BigInteger(Convert.ToInt64(Arr1[j, 0])), 
                             Convert.ToInt64(Arr1[j, 1]));
 
                if (division[0] % number != division[0].One())
                    division[0] = 
                       division[0] / new BigInteger(Convert.ToInt64(Arr1[Arr1.GetUpperBound(0), 0]));
            }
            #endregion Order Base Factor?
 
            return division[0];
        }

图 13 显示了 E_n 到 10,000 所需的时间（以十分之一秒为单位），按基底数量划分。

图 13

图 14 显示了 E_n 到 3,000 位十进制数字所需的时间（以十分之一秒为单位），按基底数量划分。

图 14

图 15

下面的图 16 是一个示例，说明了寄存器大小对计算欧拉伪素数的影响。

图 16

欧拉伪素数的因子是热尔曼素数/伪素数，而热尔曼伪素数的因子是热尔曼素数/伪素数。下面的图 17 显示了这种关系。然而，从大的欧拉数中找到热尔曼伪素数仍然非常耗时，而且与欧拉数不同，目前似乎没有直接计算热尔曼数的方法。

图 17

问题：当链接到 Access 数据库时，可能会出现以下错误：“本地计算机上未注册 ‘Microsoft.ACE.OLEDB.12.0’ 提供程序。” 要解决此问题和/或获得问题的有限解释，请访问以下链接： https://social.msdn.microsoft.com/Forums/en-US/1d5c04c7-157f-4955-a14b-41d912d50a64/how-to-fix-error-the-microsoftaceoledb120-provider-is-not-registered-on-the-local-machine?forum=vstsdb

Time32 更新数据

图 18

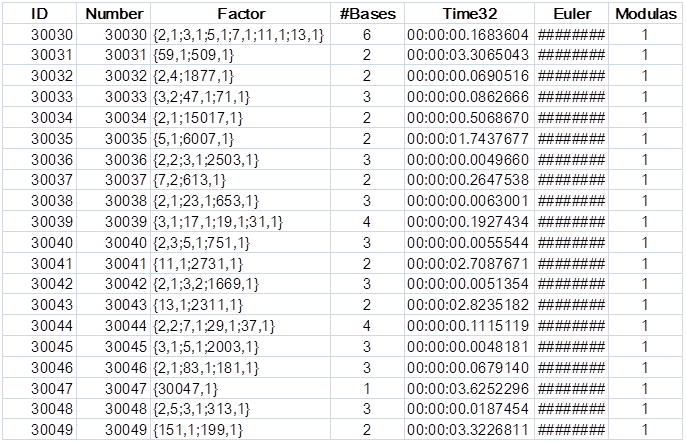
“Time32 Update Data”例程从 Excel 更新 Access 数据库，以计时生成欧拉伪素数。

图 19

Using the Code

本项目是作为一个概念原型构建的，因此它没有一个更成熟产品的用户友好错误检查。C# 代码是为 64 位系统构建的。Microsoft Office 2007 是一个 32 位环境，需要将 Excel-DNA 编译为 32 位。如果您希望此项目在 64 位 Microsoft Office 版本上运行，您将需要重新编译 Excel-DNA 以支持 64 位。BigInteger Library 已被修改以支持任意大小的整数，并且使用了 C# BigInteger Class 中的例程来扩展支持本项目所需的算法。我还修改了 BigInteger Library，增加了移位除法以提高精度，但会略微降低计算速度。BigInteger Library 中还有一些其他支持例程，我已对其进行了修改以提高其精度或支持本项目。代码应该可以用于 C# 项目、Excel VBA 和 Excel 电子表格的实验。要在 Excel 中使用，请在电子表格中打开BigInteger-packed.xll，将出现两个函数库，“BigInteger”和“Number Theory”。在 VBA 环境中引用BigInteger-packed.xll对于某些宏构建本项目使用的电子表格或在其他 VBA 应用程序中使用是必需的。Microsoft Access 和 Excel 需要引用以下库：

Visual Basic For Applications
Microsoft Access 12.0 Object Library
OLE Automation
Microsoft Office 12.0 Access database engine Object
Microsoft ActiveX Data Objects 6.1 Library
BigIntExcel

如果您使用的是 .NET 4.0 或更高版本，您可能希望修改此项目代码以使用 Microsoft 的 Numeric 库。根据我的研究，除法算法是准确性和速度的关键。

关注点

由于“RegisterSize”函数会更改静态字段的值，因此此代码不是线程安全的。通过删除此函数，应该可以相当直接地使此项目成为线程安全的。目前我还没有探索在多 CPU 环境中使用并行处理。Microsoft Excel 2007 中 BigInteger 的最大大小为 32,767 位十进制数字，如果超过此阈值，将导致计算错误。请参阅 https://support.office.com/en-us/article/Excel-specifications-and-limits-16c69c74-3d6a-4aaf-ba35-e6eb276e8eaa。

本文有两个明显的数学遗漏。查找 BigInteger 的阶的算法对于查找具有大 e 的整数的阶来说很慢。第二，正如我在本文前面提到的，（据我所知）没有直接的方法来找到 Sophie Germain 因子。然而，存在一些用于查找 Sophie Germain 因子的技术，但它们超出了本文的范围，而且这些技术对于查找大的 Sophie Germain 因子来说相当慢。注意： Jacques BASALDÚA 论文的链接已失效。我没有重新发布它们。他需要自己重新发布。另外，D:\BaseASeq\ProgramsC#\ExcelDna-0.32\Distribution\ExcelDnaPack.noexe 在编译 C# 代码之前应更改为 .exe。我已删除 ExcelDNA 中的所有 .exe 文件，因此如果您需要它们，则需要重新编译或从原始 zip 文件中解压缩。

历史

这是该软件的第一个版本。