从平稳性到混沌的随机性

• 下载 R 源代码和示例文件 - 1 MB

引言

本文的目的是，除了对复杂性和随机性进行一些数学哲学思考外，还可以利用开源免费的统计程序 R，对分析复杂时间序列的一些有用技术进行简要回顾。

如果您更喜欢本文的西班牙语版本，可以访问我的博客。

背景

存在一些非常简单的数学模型，仅通过改变一个参数，我们就可以得到一系列具有从平稳到混沌的广泛动态行为的时间序列，其中还包含不同程度的周期性。

这类模型的典型例子是逻辑斯谛方程，这是一个非常简单的迭代函数，其数学表达式如下：

X_n+1 = UX_n(1-X_n)

该方程的值域是 (0, 1) 开区间，而参数 U 的取值范围是 (0, 4) 开区间。当 U 参数接近 0 时，生成的时间序列是完全平稳的，只取一个值；但当 U 达到临界点 3 时，突然变为周期性的，交替取两个不同的值。

随着 U 参数值的升高，直到大约 3.5699，值的数量（即周期）会翻倍，当达到这个极限值时，再次达到一个临界点，时间序列的动态就会变得混沌。

混沌的程度随着 U 参数的增加而增加（除了某些特殊的周期性岛屿点），直到 U = 4，此时时间序列发散到无穷大。

但是，我们可以更进一步，尝试达到随机性，使用相同的确定性过程，正如您将在文章结尾看到的。

另一个可用于研究这类过程的简单系统是三角映射，其表达式如下：

X_n+1 = U(1 – 2|0.5 - X_n|)

在这个方程中，参数 U 的取值范围是 (0, 1) 开区间。

Using the Code

样本代码包含源代码文件 beyond-chaos.R 中的一些 R 函数。

#########################################################################
#
# Logistic equation
# u: parameter
# length: number of terms in the series
# initial: initial value for the series
#
#########################################################################
fLog<-function(u,length,initial) {
 c<-1:(length+300);
 c[1] <- initial;
 for (i in 2:(length+300)) {
  c[i]<-u*c[i-1]*(1-c[i-1]);
 }
 return(c[-(1:300)]);
}
#########################################################################
#
# triangular application
# u: parameter
# length: number of terms in the series
# initial: initial value for the series
#
#########################################################################
fTriangular<-function(u,length,initial) {
 c<-1:(length+300);
 c[1] <- initial;
 for (i in 2:(length+300)) {
  c[i]<-u*(1-2*abs(0.5-c[i-1]));
 }
 return(c[-(1:300)]);
}
#########################################################################
#
# Normal random time series promediating chaotic series
# u1: parameter for the seeds series
# u2: parameter for the promediated series
# seed: initial value for the seed series
# length: number of terms in the returned series
# count: number of series to promediate
# fr: function to promediate (fLog or fTriangular)
#
#########################################################################
randFunc<-function(u1,u2,seed,length,count,fr) {
 v<-fr(u1,count,seed);
 x<-rep(0,length);
 for(i in 1:count) {
  x = x+fr(u2,length,v[i]);
 }
 return(x/count);
}
#########################################################################
#
# Logistic helper for web diagram
# u: parameter
# x: value of Xn
#
#########################################################################
fWebLog<-function(u,x) {
    return (u*x*(1-x));
}
#########################################################################
#
# Triangular helper for web diagram
# u: parameter
# x: value of Xn
#
#########################################################################
fWebTriangular<-function(u,x) {
    return (u*(1-2*abs(0.5-x)));
}
#########################################################################
#
# Draws a web diagram
# p: parameter
# steps: number of terms of the time series to draw
# fw: function to use (fWebLog or fWebTriangular)
#
#########################################################################
webDiagram<-function(p, steps=500, fw) {
    xn<-seq(0,1,length.out=1000);
    xn1<-sapply(xn,fw,u=p);
    plot(xn,xn1,type='l',col="red");
    lines(xn,xn,lty=4);
    x0<-runif(1);
    xn<-x0;
    xn1<-0;
    for (i in 1:steps) {
        xf<-fw(p, x0);
        xn<-c(xn,x0);
        xn1<-c(xn1,xf);
        xn<-c(xn,xf);
        xn1<-c(xn1,xf);
        x0<-xf;
    }
    lines(xn,xn1);
}
#########################################################################
#
# draws a Feyenbaun diagram of bifurcation
# start: first value of the parameter
# end: final value of the parameter
# step: increment in the parameter
# fw: function to use (fLog or fTrangular)
#
#########################################################################
feigenbaum<-function(start,end,step,fw) {
 pu<-seq(start,end,by=step);
 orbit<-sapply(pu,fw,initial=0.1,length=300);
 r<-sort(rep(pu,300));
 plot(r,orbit,pch=".");
}
#########################################################################
#
# draws a recurrencePlot for the RP property of the result of crqa function
# rp: RP property of the object (recurrence plot)
#
#########################################################################
recurrencePlot<-function(rp) {
 x<-rep(1:(dim(rp)[1]),dim(rp)[2])[as.vector(t(rp))==T];
 y<-as.vector(sapply(1:(dim(rp)[2]),rep,dim(rp)[1]))[as.vector(t(rp))==T];
 plot(x,y,pch=".",pty="s",asp=1);
}
#########################################################################
#
# Helper to build a dataframe with delayed time series to train
# recurrent neural networks
# data: original time series
# lags: number of delayed versions of the original time series
#
#########################################################################
lagTS<-function(ts,lags) {
 y<-as.zoo(ts);
 for (l in 1:lags) {
  y<-cbind(y,Lag(y,k=l));
 }
 return(na.omit(y));
}

从 zip 文件中解压后，只需使用 R 命令 source 加载它。

source("beyond-chaos.R")

探索混沌

这些系统的动态的平稳和周期区域没有什么有趣的特性可供检查，所以，只考虑它们是 U 参数某些值的可能状态，然后我们来更详细地看看混沌区域。

为了了解系统随着参数变化的行为，我们可以绘制一个 Feigenbaum 图，在那里你可以清楚地看到序列值的分岔以及直到混沌区域的值集的增长。

为此，请使用 feigenbaum 函数（改编自R-bloggers 的这篇博文）。参数包括参数 U 的值区间的起始和结束点、参数的增量步长以及您想要用于生成数据的函数。

这个函数可以是两个之一：fLog，用于绘制逻辑斯谛方程的分岔图；或 fTriangular，用于绘制三角映射的相应图。这两个函数会在序列的开始处计算 300 个额外的项，这些项会被丢弃以消除暂态动态状态。

例如，对于逻辑斯谛方程：

feigenbaum(2.5,4,0.003,fLog)

可以使用一个称为网络图（web diagram）的图形工具来检查动态的复杂程度。这种图的绘制方式如下：首先，我们绘制函数在整个值区间（在此例中为 0 到 1 之间）的曲线，然后，我们绘制直线 y = x。我们取 x 轴上的任意一个值，并从这里向函数曲线绘制一条垂直线。从这里，一条新的水平线到 y = x 线，然后，从这里，再次向上绘制一条垂直线到曲线。这个过程会重复一定次数。

要绘制此图，您可以使用 webDiagram 函数。参数是给定函数的 U 参数、绘制的步数以及用于获取值的函数。您可以使用 fWebLog 和 fWebTriangular 函数来绘制逻辑斯谛或三角函数的网络图。

例如，这是逻辑斯谛方程周期性序列的网络图。

webDiagram(3.4,fw=fWebLog)

这是三角映射混沌区域的另一个网络图。

webDiagram(0.99,fw=fWebTriangular)

如果您想了解更多关于网络图的信息，可以访问我的博客。

复杂系统的第一个有趣的特性是它们对初始条件的**敏感性**。由于这些系统是确定性的，如果您生成一些时间序列，总是从完全相同的初始值开始，那么您将总是得到完全相同的时间序列。但如果您改变一点点初始值，您将得到完全不同的时间序列。

例如，看看使用逻辑斯谛方程以 0.1 和 0.1001 作为初始值绘制两个时间序列会发生什么。

plot(fTriangular(0.95,100,0.1),type="l")
lines(fTriangular(0.95,100,0.1001),col="red")

在这种情况下，我使用了三角映射，并配合 fTriangular 函数，U 参数为 0.95，生成了 100 个序列项。您可以使用 fLog 函数和 U 参数 3.98 等来获得类似的结果，以生成混沌序列。

这种对初始条件的敏感性使得自然复杂系统的状态几乎无法重现，并且大大限制了预测的可能性，除了非常短的时间。

但是，这些过程的确定性性质可以通过使用神经网络来拟合生成时间序列的函数来检验。例如，我将使用 R 的 RSNNS 包，结合循环 Elman 神经网络。

我用来拟合时间序列的神经网络的程序是使用一个数据集对其进行训练，该数据集由一些列组成，其中每列都是同一时间序列延迟一项。这样，在每一行中，我们都有当前项以及 n 个前项。为此，我使用 lagTS 函数，该函数接受时间序列和要构建的先前项的数量，并返回一个 dataframe，其第一列包含要预测的序列。（关于循环神经网络的更多信息，可以在我的博客中找到）。

require(RSNNS)
require(quantmod)
tsl<-fLog(3.98,1000,0.2)
y<-lagTS(as.ts(tsl),10)
train<-1:900
inputs<-y[,2:11]
outputs<-y[,1]
fit<-elman(inputs[train],outputs[train],size=c(3,2),
    learnFuncParams=c(0.1),maxit=1000)
pred<-predict(fit,inputs[-train])

我使用前 900 行来训练网络，然后使用训练好的网络对剩余的 90 个值进行预测。这是要预测的 90 个序列项。

plot(as.vector(outputs[-train]),type="l")

这是神经网络预测的序列，叠加在原始序列之上，用红色表示。

lines(pred,col="red")

看起来神经网络可以完美预测混沌系统，但事实并非如此。如果您尝试预测序列的下一个项以外的内容，结果会很快失去准确性。但重要的是要指出，由于过程的确定性特征，网络能够很好地逼近原始函数。让我们看看最无序的序列，也就是随机序列会发生什么。

您可以使用 rnorm 等函数来生成正态分布的随机序列，但这些函数通常是伪随机数生成器，它们也使用确定性过程来获取值。与之不同，我将从这个网站获取一个真正随机的时间序列，该网站使用大气噪声来生成序列。（实际上，使用一个好的伪随机数生成器，您会得到几乎相同的结果，但这种方式更严格。）

我获得了一个具有均匀分布的大气白噪声样本。在一个 wav 音频文件中。所以我会使用 audio 包来读取它。

require(audio)
wv<-load.wave("soundfile.wav")

然后，我重复之前的过程，但首先将数据归一化到 0 到 1 之间的值，以便网络工作得更好。

tsr<-(wv[1:1000] - min(wv[1:1000]))/(max(wv[1:1000])-min(wv[1:1000]))
y<-lagTS(as.ts(tsr),10)
inputs<-y[,2:11]
outputs<-y[,1]
fit<-elman(inputs[train],outputs[train],size=c(3,2),
    learnFuncParams=c(0.1),maxit=1000)
pred<-predict(fit,inputs[-train])
plot(as.vector(outputs[-train]),type="l")
lines(pred,col="red")

并不容易，是吗？我们能否无限提高这些系统的复杂性？因为当 U 参数达到最大值时，系统就会发散到无穷大。

从混沌到随机

看起来我们无法无限提高这些系统的复杂性，因为当 U 参数达到最大值时，系统就会发散到无穷大。

仅使用一个序列是无济于事的，但如果我们使用多个呢？如果您还记得中心极限定理，如果您将一些服从相同分布的变量相加，最终的分布会趋向于正态分布（即随机）。您可以使用它们的初始条件敏感性来生成多个完全不同的时间序列，使用相同的 U 参数，然后对它们进行平均。

为此，我编写了 randFunc 函数，其参数如下：u1 是我将用于生成初始值的某个时间序列的 U 参数；u2 是生成的 N 个时间序列的 U 参数；seed 是初始值的种子；length 是最终时间序列的长度；count 是要平均的序列数量；最后，fr 是要使用的函数（fLog 或 fTriangular）。

您可能会认为我们需要平均很多序列才能得到一个随机序列。让我们用五个试试。

r5<-randFunc(3.9,3.99,0.2,1000,5,fLog)

现在，我们进行一些正态性检验。

shapiro.test(r5)
W = 0.99781, p-value = 0.2119
qqnorm(r5)
qqline(r5)

看起来一切都很好，不是吗？但此外，我将尝试使用更复杂的工具——重构图（recurrence plot）来寻找确定性的痕迹。我将为此使用 crqa 包。

重构图并非易事，如果您想了解更多关于它的信息，可以访问我的博客。为了了解我正在搜索的内容，让我们先看看使用逻辑斯谛方程绘制的确定性系统的重构图。

Require(crqa)
tsl<-as.ts(fLog(3.98,198,0.2))
rqa<-crqa(tsl,tsl,delay=1,embed=1,rescale=0,radius=0.03,
    normalize=0,mindiagline=2,minvertline=2,side="both")

返回的 rqa 对象包含一些用于进行重构分析的属性和值。其中一个是 RP，它包含重构图本身。我不知道直接绘制它的方法，所以，我编写了 recurrencePlot 函数来完成这个任务。调用方式如下：

recurrencePlot(rqa$RP)

这张图的关键在于，除了可识别的方形结构外，对角线是确定性系统的特征。rqa 对象有一个属性称为确定性率或 DET，该序列的值为：

rqa$DET
68.86727

将此与随机大气噪声的重构图进行比较：

tsl<-as.ts(wv[1:200])
rqa<-crqa(tsl,tsl,delay=1,embed=1,rescale=0,radius=0.05,
    normalize=0,mindiagline=2,minvertline=2,side="both")
recurrencePlot(rqa$RP)

正如您所见，确定性结构已经消失，点主要是孤立的，而不是形成对角线。DET RQA 度量也比前一种情况低得多。

rqa$DET
9.7621

那么，假设从逻辑斯谛方程获得的随机序列怎么样？这是相应的重构图。正如您所见，与真正随机时间序列的重构图没有明显区别。

tsl<-as.ts(r5[1:200])
rqa<-crqa(tsl,tsl,delay=1,embed=1,rescale=0,radius=0.01,
    normalize=0,mindiagline=2,minvertline=2,side="both")
recurrencePlot(rqa$RP)

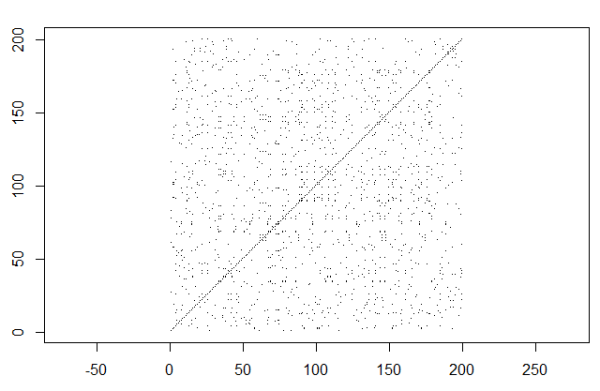
DET 度量也和随机序列一样低。

<span style="line-height: 115%; font-family: "Courier New"; font-size: 11pt"><font color="#000000">rqa$DET
8.093995</font></span>

由此我们可以得出的一个结论是，数据的随机性，甚至它们的噪声，可能仅仅是一种幻觉，由于测量过程的分辨率不足以区分所有涉及的变量。

考虑到这一点，以及简约原则，大自然中真的存在随机性吗？或者复杂性足以解释它，而我们必须将随机性视为测量仪器不足的结果？

感谢大家的阅读！！！