编码挑战:最小圆问题
4.86/5 (20投票s)
思考算法...
引言
我们大多数人在大多数时候都使用现成的库/函数进行计算,这些库/函数已经实现了解决我们问题的最佳算法。只有少数人会进行数学脑力练习,为新问题或情况创建算法。我们现在将做的正是如此……在不查阅我们最喜欢的搜索引擎的情况下,仅凭我们自己的大脑和一些基本数学知识来构建一个算法。
包围一组点集中的最小圆问题是一个古老(约150年)的数学问题,但至今仍未有完美的解决方案……为了寻找一个快速的解决方案,不同的人创建了不同的算法,执行时间各不相同,例如 O(n<sup>4</sup>)、O(h<sup>3</sup>n)、O(n log n),最终——在大约30年前——O(n)。
在本文中,我们将创建一个 O(n) 的算法,这可能是最快的算法之一……
使用代码
文章中的代码示例来自附件代码,无法直接执行——您需要支持输入和输出的代码……要获得完整解决方案,请下载附件的项目,该项目使用 VS Code 和 .NET Core 创建(因此您也可以在 Linux 或 Mac 上使用)。
基础
关于开发人员是否应该学习数学,以及学习到什么程度,这是一个长期的争论。然而,对于这个问题,您必须了解一些基础知识,才能在没有适当数学证明的情况下理解我(是的,我不会深入详细的数学证明,因为这可能会写成一本书)。
为了简单起见,我们假设一些
- 集合中至少有三个点
- 集合中的任何三个点都不会形成一条直线
您必须了解/理解
- 三个点(一个三角形)定义唯一的圆
- 圆由其中心和半径定义,因此圆上的点被视为在圆内
- 您必须理解简单的向量计算,例如两点之间的距离、两个向量的交点……(或者至少相信我提供的公式)
特殊情况
这是点集小于四个点的情况。对于这些情况,每种情况都有一个精确的解决方案
- 一个点:该点本身就是圆心,半径为零
- 两个点:圆心是连接两点的向量的中点,半径是该向量长度的一半
- 三个点:形成一个三角形,解决方案是外接圆(通过所有三个点的圆)
- 形成一条直线的三个点:这类似于两点的情况,在丢弃中间点之后
虽然这些情况都有解决方案,但我不希望将它们包含在代码中,因为我想专注于我们主要算法的开发……
审视问题
这个问题最有趣的部分是,人类只需看着点集就能很容易地解决它。然而,计算机不会看,也不会看见。例如,看看下面的点集,给自己几分钟时间,您就会发现哪些是定义包围圆的关键点。

最直接的解决方案 - 暴力法
基本思想是遍历点集中的点,并扩展初始圆以包含它们。起始圆由集合中的前三个点(外接圆)构成,因此实际的遍历从第四个点开始……
因此,在每一步,我们都有一个圆,由前一步的三角形和一个新点构成。想法是用新点替换离新点最近的点,然后重新计算外接圆……这种方法是完全线性的,因为我们只遍历每个点一次,所以执行时间仅取决于点集中的点数。
让我们看看代码的主要部分
public static Circle BruteForce(Set Set)
{
Circle oCircle = new Circle();
oCircle.Init(Set[0], Set[1], Set[2]);
for (int nIndx = 3; nIndx < Set.Count; nIndx++)
{
Point oNew = Set[nIndx];
double nD = Math.Sqrt(Math.Pow(oCircle.O.X - oNew.X, 2) + Math.Pow(oCircle.O.Y - oNew.Y, 2));
Dictionary<double, Point> oSel = new Dictionary<double, Point>();
if (nD > oCircle.R)
{
oSel.Add(Math.Sqrt(Math.Pow(oCircle.A.X - oNew.X, 2) + Math.Pow(oCircle.A.Y - oNew.Y, 2)), oCircle.A);
oSel.Add(Math.Sqrt(Math.Pow(oCircle.B.X - oNew.X, 2) + Math.Pow(oCircle.B.Y - oNew.Y, 2)), oCircle.B);
oSel.Add(Math.Sqrt(Math.Pow(oCircle.C.X - oNew.X, 2) + Math.Pow(oCircle.C.Y - oNew.Y, 2)), oCircle.C);
List<double> oList = oSel.Keys.ToList();
oList.Sort();
oSel[oList[0]] = oNew;
oCircle = new Circle();
oCircle.Init(oSel[oList[0]], oSel[oList[1]], oSel[oList[2]]);
}
}
return (oCircle);
}
由三个点创建的圆(通过 Init 方法)。我使用每个点到新点的距离作为索引来选择要替换的点并重新计算圆。我跳过已经位于当前圆内的点……
让我们看看结果

D 后的圆,蓝色圆是添加 E 后的圆。
F 被跳过,因为它在添加 E 后已经位于圆内。
现在,这是一个不错、可靠的解决方案,但只有一个问题——并不总是给出正确答案……
让我们看看另一个点集及其结果

D 被跳过,因为它已经在圆内,但添加 E 时一切都错了……
圆(绿色弧线)太大了,而 D 在它外面……
从结果来看,人们可能会得出结论,与其替换离新点最近的点来创建新圆,不如创建两个可能的圆(我们不使用最远的点,因为它只会镜像圆而不是扩展它),然后选择最小的那个。
这是这种暴力破解版本的代码
public static Circle BruteForce2(Set Set)
{
Circle oCircle = new Circle();
oCircle.Init(Set[0], Set[1], Set[2]);
for (int nIndx = 3; nIndx < Set.Count; nIndx++)
{
Point oNew = Set[nIndx];
double nD = Math.Sqrt(Math.Pow(oCircle.O.X - oNew.X, 2) + Math.Pow(oCircle.O.Y - oNew.Y, 2));
Dictionary<double, Point> oSel = new Dictionary<double, Point>();
if (nD > oCircle.R)
{
oSel.Add(Math.Sqrt(Math.Pow(oCircle.A.X - oNew.X, 2) + Math.Pow(oCircle.A.Y - oNew.Y, 2)), oCircle.A);
oSel.Add(Math.Sqrt(Math.Pow(oCircle.B.X - oNew.X, 2) + Math.Pow(oCircle.B.Y - oNew.Y, 2)), oCircle.B);
oSel.Add(Math.Sqrt(Math.Pow(oCircle.C.X - oNew.X, 2) + Math.Pow(oCircle.C.Y - oNew.Y, 2)), oCircle.C);
List<double> oList = oSel.Keys.ToList();
oList.Sort();
Circle oC1 = new Circle();
oC1.Init(oSel[oList[0]], oNew, oSel[oList[2]]);
Circle oC2 = new Circle();
oC2.Init(oNew, oSel[oList[1]], oSel[oList[2]]);
oCircle = oC1.R < oC2.R ? oC1 : oC2;
}
}
return (oCircle);
}
但看看下一个样本集,我们发现它也毫无用处……
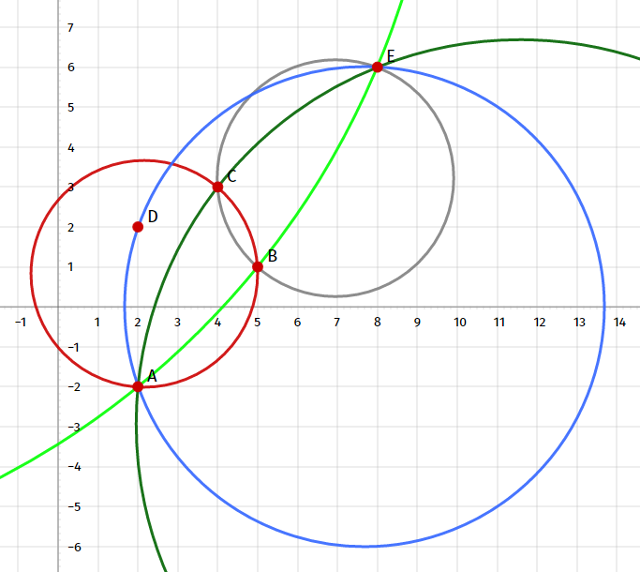
D 被跳过,因为它已经在圆内。
我们比较了圆 ACE(深绿色弧线)和 ABE(浅绿色弧线),发现 ACE 更小,然而真正的解决方案是蓝色圆。
到目前为止——使用纯粹的直觉和简单的逻辑——我们一无所获,是时候加入更多内容了……
走向真正的解决方案
在与计算机打交道一段时间后,我们习惯于将问题视为一个机器,并将其分解以便机器能够处理。在某些情况下——就像这个——它并不如预期那样奏效……所以我邀请您重新思考我们的方法……
停顿一下,试着回忆一下您是如何解决我给您的第一个样本的(当我让您观察并解决时)。我个人是通过消除点集中的内部点,并将注意力集中在周长上的点来解决的。只处理那些点给了我一个即时解决方案……
因此,我得出结论,我们不应该使用点集中的所有点来找到最小圆,而应该只使用那些位于点集周长上的点。很容易理解,那些位于点集中心区域的点在最终结果中不起实际作用,而位于周长上的点才是重要的。
为了找到周长上的点,我引入了一个新问题(不要惊慌——它有一个最简单的解决方案):包围所有点的最小矩形。
要确定矩形,我们只需要扫描点集,找到点的 X 和 Y 坐标的最大值和最小值。
现在,很容易看出并理解一个穿过该矩形所有四个边缘点的圆也会包围点集中的所有点。因此,所有位于最小矩形内的点也都会位于最小圆内,而那些位于最小矩形上的点,要么位于最小圆上,要么位于最小圆内。
然而,这不一定是最小的圆,因为——取决于点在矩形上的位置——其中一些点可能在圆上而不是在圆内……

所以这个解决方案有两个步骤
- 从点集中移除所有无关点
- 对剩余点运行简单的暴力破解
这里是代码
public static Circle BruteForceFixed(Set Set)
{
Set oSet = new Set();
oSet.AddRange(Set);
oSet.RemoveAll(oPoint =>
(oPoint.X < oSet.Max(oTemp => oTemp.X)) &&
(oPoint.X > oSet.Min(oTemp => oTemp.X)) &&
(oPoint.Y < oSet.Max(oTemp => oTemp.Y)) &&
(oPoint.Y > oSet.Min(oTemp => oTemp.Y)));
List<Point> oEdges = oSet.FindAll(oPoint =>
((oPoint.X == oSet.Max(oTemp => oTemp.X)) && (oPoint.Y == oSet.Max(oTemp => oTemp.Y))) ||
((oPoint.X == oSet.Max(oTemp => oTemp.X)) && (oPoint.Y == oSet.Min(oTemp => oTemp.Y))) ||
((oPoint.X == oSet.Min(oTemp => oTemp.X)) && (oPoint.Y == oSet.Max(oTemp => oTemp.Y))) ||
((oPoint.X == oSet.Min(oTemp => oTemp.X)) && (oPoint.Y == oSet.Min(oTemp => oTemp.Y)))
);
if(oEdges.Count >= 2)
{
oSet.Clear();
oSet.AddRange(oEdges);
}
if (oSet.Count == 2)
{
oSet.Add(new Point() { X = oSet[0].X, Y = oSet[1].Y });
}
return (BruteForce(oSet));
}
这段代码处理了您可能已经问过的特殊情况……由两个边缘点定义的最小矩形……这当然会导致我们之前提到的特殊情况之一,为了克服它,我添加了一个第三个——虚构的——点到集合中,一个第三个边缘点……
我还考虑了集合中至少有两个最小矩形边缘点的情况——在这种情况下,所有其他点都无关紧要,对它们运行暴力破解将给出错误的答案……
但是看!即使这个解决方案也无法拯救我们。看看这个点集

H 在蓝色圆之外!
结束
总结一下我们到目前为止学到的
- 对点进行简单遍历并不能解决所有点集
- 识别最小矩形只在周长上的点实际定义该矩形的情况下才有帮助(意味着其中至少两个是边缘点)
从这一切中,我们可以确定两种情况
- 由两个点定义的最小圆
- 由三个点定义的最小圆
我们已经为每种情况确定了一些场景,但总是发现漏洞。然而,看看最后一个点集和下面的点集,我们可以发现一些非常重要的事情。

D 在它外面!
从这些图像中,我们可以构想一个定义,它可以帮助我们决定何时使用两个点,何时使用三个点来定义集合的周长。
一个结论是,点将来自距最小矩形中心最远的三个点集。要判断我们将使用所有三个还是仅使用其中两个,我们需要检查它们之间每对点的距离。我们正在寻找这些距离中最长的一个,以检查它是否足够长可以作为圆的直径……如果足够长,那么我们只需要这两个点来定义圆,否则我们需要三个点。
我们如何知道它足够大?如果第三个点到中心的距离小于该距离的一半,那么即使是第三个点也位于最小圆内……让我们在图上看看

A、B 和 C 是距矩形中心最远的点。然而,B 的距离小于 A 和 C 之间距离(此三点中最大的)的一半,所以我们只需要由 A 和 C 定义的圆!

E、F 和 H 是距矩形中心最远的点。E 的距离大于 F 和 H 之间距离(此三点中最大的)的一半,所以我们也需要由 E、F 和 H 定义的圆!
所以解决方案如下
- 找到最小矩形的中心点
- 找到距该中心最远的三个点
- 如果最小矩形的边缘上有两个点,那么这两个点也定义了最小圆
- 如果最小计算机的边缘上有一个点,那么我们就有三个点来定义圆
- 否则,将该三角形的最长边与第三个点到中心的距离进行比较,以确定有多少点定义了最小圆
- 计算圆
所有这些组合在一起的代码
public static Circle BruteForceFinal(Set Set)
{
Set oSet = new Set();
Circle oCircle = new Circle();
Point oO = new Point()
{
X = ((Set.Max(oPoint => oPoint.X) + Set.Min(oPoint => oPoint.X)) / 2),
Y = ((Set.Max(oPoint => oPoint.Y) + Set.Min(oPoint => oPoint.Y)) / 2)
};
oSet.AddRange(Set.OrderByDescending(oPoint => Math.Sqrt(Math.Pow(oPoint.X - oO.X, 2) + Math.Pow(oPoint.Y - oO.Y, 2))).Take(3));
List<Point> oEdges = oSet.FindAll(oPoint =>
((oPoint.X == Set.Max(oItem => oItem.X)) && (oPoint.Y == Set.Max(oItem => oItem.Y))) ||
((oPoint.X == Set.Max(oItem => oItem.X)) && (oPoint.Y == Set.Min(oItem => oItem.Y))) ||
((oPoint.X == Set.Min(oItem => oItem.X)) && (oPoint.Y == Set.Max(oItem => oItem.Y))) ||
((oPoint.X == Set.Min(oItem => oItem.X)) && (oPoint.Y == Set.Min(oItem => oItem.Y)))
);
Console.Write("Edges: ");
foreach (Point oPoint in oEdges)
{
Console.Write(string.Format("({0}, {1})", oPoint.X, oPoint.Y));
}
Console.WriteLine();
if (oEdges.Count == 2)
{
oSet.Clear();
oSet.AddRange(oEdges);
}
else if (oEdges.Count == 0)
{
Dictionary<double, Point> oTemp = new Dictionary<double, Point>();
oTemp.Add(D(oSet[0], oSet[1]), oSet[2]);
oTemp.Add(D(oSet[0], oSet[2]), oSet[1]);
oTemp.Add(D(oSet[1], oSet[2]), oSet[0]);
KeyValuePair<double, Point> oLarge = oTemp.OrderByDescending(oItem => oItem.Key).First();
if (oLarge.Key > D(oLarge.Value, oO))
{
oSet.Remove(oLarge.Value);
}
}
if (oSet.Count == 2)
{
oSet.Add(new Point() { X = oSet[0].X, Y = oSet[1].Y });
}
oCircle.Init(oSet[0], oSet[1], oSet[2]);
return (oCircle);
}
这就是最后的结论……
摘要
我没有花太多时间来分享我的陈述的数学证明,也没有解释计算两条线交点的相当复杂的代码(您只能在附件代码中看到它),这是因为我的重点更多地是让您意识到,一个好的算法涉及将机器般的思维与人类思维相结合。
最后几点
如果您对最终解决方案的 O(n) 性质有疑问,请考虑这一点:O(n) 意味着唯一改变执行时间的因素是我们遍历的元素数量。因此,即使我们进行两次或多次遍历,我们在每次遍历中都只访问每个元素一次,所以我们仍然是 O(n)。
关于图片的说明。如果您需要创建此类图片,请搜索“scetchometry”。它是免费且非常棒的……
