点集的凹包

Alasdair Craig

4.96/5 (30投票s)

2017年8月16日

CPOL

8分钟阅读

72309

5323

一种使用 k-最近邻方法的凹壳计算已发布算法的 C++ 实现。

引言

该算法在 A. Moreira 和 M. Santos 于 2007 年在葡萄牙米尼奥大学发表的论文《Concave Hull: A k-nearest neighbours approach for the computation of the region occupied by a set of points》中有描述。

我在未优化的算法上取得了显著的性能提升。我认识到使用 Flann 库进行 k-最近邻搜索和 OpenMP 并行化进行点在多边形内测试将使该算法受益。本文演示了我的发现，例如什么会影响计算时间。

我对数据集变大时的性能感到好奇。我使用地面点数据集，例如航空激光雷达扫描的数据集，作为测试数据集。我的程序轻量级，仅依赖于 Flann。

示例

下面的示例显示了一个点集，其中蓝色多边形是计算出的凹壳。

示例 1： 771 个输入点，166 个凹壳点，计算时间 0.0 秒。

示例 2： 4726 个输入点，406 个凹壳点，计算时间 0.1 秒。

示例 3： 54323 个输入点，1135 个凹壳点，计算时间 0.4 秒。

示例 4： 312428 个输入点，1162 个凹壳点，计算时间 26.0 秒（参见下文的分析部分）。

工作原理

Moreira-Santos 算法是一种迭代解决方案，其中初始最近邻 K 值设置为 3，并 iteratively 增加，直到找到一个包围所有点的多边形。这就是凹壳。进一步增加 K 会使壳体更平滑，但可能使其不太美观。

当 k-最近邻搜索使用 K=3 时，这意味着找到任何测试点最近的三个点。太小的 K 意味着找不到包围的壳体。太大的 K 可能意味着壳体中重要的凹陷被平滑掉了。

算法在第一个生成有效凹壳的 K 值处停止。我的程序有一个命令行参数，可以传递一个更高的 K 值来生成更平滑的多边形（如果需要）。理想情况下，应该进行一些视觉检查，以确定确定壳体的第一个 K 值是否足够，或者增加的 K 值是否能产生更令人愉悦的结果。

请参阅下文的寻找性能部分，了解我如何实现比未优化算法更高的性能。

分析

从 K=3 开始计算壳体所需的时间与输入点的数量大致呈线性关系。然而，其他因素也会影响绝对运行时间。由于这些因素，n 个点的某个数据集的计算时间不会与另一个 n 个点的数据集相同。

输入点的数量

所有点都需要通过点在多边形内测试才能停止迭代。因此，输入点越多，该测试就会越慢。我尝试通过并行化点在多边形内测试的输入来最小化这一点。

边缘附近的点间距，无论是均匀的还是存在较大差异

边缘附近点的几何形状会影响 K 迭代。如果边缘“混乱”，则需要检查更多的邻近点 (K)；如果边缘在点密度和间距方面变化很小，则情况则不同。规则网格的点将比无序和不规则的点集具有更快的计算时间。上面的示例 4 是一个例子，其中由于点间距非常不规则，K 需要达到 50+ 才能完成。

达到解所需的 K 迭代次数

如上（2）所示，迭代次数越多，点在多边形内测试可能需要执行的次数就越多，这是两个迭代步骤标准之一。（参见下文寻找性能部分的可能优化。）

壳体多边形的大小

点在多边形内测试对于具有许多顶点的壳体多边形会比多边形较小的情况慢，尽管这比传递给测试的点数更不重要。

瓶颈

在我的代码中，在许多性能改进之后（参见下文寻找性能部分），性能分析显示最大的瓶颈是点在多边形内检查。此测试是迭代的停止条件。如果数据集中有任何点不在该迭代中计算出的多边形内，则 K 将被递增。因此，点在多边形内测试至关重要，但成本很高。

大型示例的基准测试

我专注于大型输入数据集。以下是三个示例，其中我以 100,000 为增量直到一百万进行测试。这是为了比较输入点大小和 K 迭代次数对计算时间的影响。

大型示例 1： 995165 个输入点，5221 个凹壳点，计算时间 10.7 秒。

大型示例 2： 984119 个输入点，4907 个凹壳点，计算时间 16.8 秒。

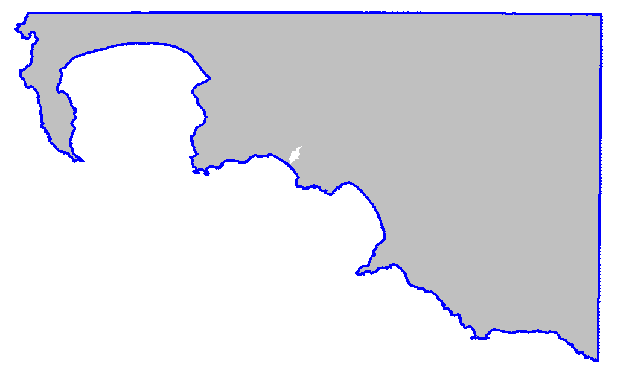
大型示例 3： 998817 个输入点，8787 个凹壳点，计算时间 31.1 秒。

对于大型数据集，此算法仍然可能很有用，如果它首先被降采样到更易于管理的尺寸，然后再计算凹壳。但这只有在凹壳不需要对原始数据集的边缘进行精确计算时才可能。

以上计时是在 Core i7-2600 @3.4 GHz、16GB RAM、Windows 10 上进行的。

寻找性能

我发现的性能提升按影响顺序排列

使用 Flann 进行最近邻点搜索为我带来了最直接的性能提升。
论文中的算法要求频繁从数据集中删除点。最初，我发现使用 std::vector::erase 来做同样的事情是一个主要的瓶颈。我完全放弃了那种存储方式，因为 Flann 的方式已经存储了点并且能够标记点为已删除。
测试是否有任何点未能通过点在多边形内测试是并行化的理想选择。我使用了 any_of 的 OpenMP 并行实现。
除了 2D 坐标之外，我还为每个点存储了一个唯一的 ID，它保持排序，允许我通过二进制搜索查找点 ID，而不是通过值语义进行搜索。

我预见的可能值得的优化，但未尝试过

可以通过选择一个更大的增量来更快地找到最终的 K，而不是只增加 1，从而更快地找到一个有效的，但过于平滑的多边形，然后以类似二分查找的方式递减 K 来收敛。
计算每个点在点在多边形内测试中通过的次数，然后按此数量排序，首先测试那些在前一次迭代中从未通过的点。想法是，如果它以前通过过，它很可能再次通过。

使用代码或程序

构建代码

除了 Flann 库调用和一点 OpenMP 外，代码是标准的 C++，大量依赖 STL 算法。Flann 也需要单独安装，但之后它只是一个头文件。我使用 Visual Studio 构建了这个程序，但它也可以使用任何符合 C++11 标准的编译器构建。

运行可执行文件

如果您收到系统错误，提示程序无法启动，因为缺少 VCOMP140.dll、MSVCP140.dll 或 VCRUNTIME140.dll，则需要下载并安装 Microsoft Visual C++ 2015 Redistributable。

命令行用法如下

Usage: concave.exe filename [-out arg] [-k arg] [-field_for_x arg] [-field_for_y arg] [-no_out] [-no_iterate]

 filename     (required) : file of input coordinates, one row per point.
-out          (optional) : output file for the hull polygon coordinates. Default=stdout.
-k            (optional) : start iteration K value. Default=3.
-field_for_x  (optional) : 1-based column number of input for x-coordinate. Default=1.
-field_for_y  (optional) : 1-based column number of input for y-coordinate. Default=2.
-no_out       (optional) : disable output of the hull polygon coordinates.
-no_iterate   (optional) : stop after only one iteration of K, irrespective of result.

唯一必需的参数是输入坐标的 filename。输入文件中的字段可以是逗号、制表符或空格分隔。相邻的空格被视为一个。默认情况下，前两个字段用于 x 和 y，但这可以通过 -field_for_x 和 -field_for_y 参数进行更改。凹壳坐标的输出默认到 stdout，但可以通过 -out 参数重定向到文件。在这种情况下，输出是空格分隔的，除非文件名具有 .csv 扩展名，使其成为逗号分隔。-k、-no_out 和 -no_iterate 参数主要用于分析/测试目的，但它们不言自明。

与 alpha-shapes 的比较

Alpha-shapes 是通常提到的确定凹壳的方法。CGAL、PCL（点云库）和 LASLib 中提供了 alpha-shapes 的 C++ 实现。然而，这些要么有对商业不友好的许可要求，要么有非常繁琐的构建依赖项，如果不需要的话，这些依赖项是无法承受的。

我仍然将我的程序性能与 PCL 的 alpha-shape 实现 pcl::ConcaveHull<> 进行了比较。我发现 Moreira-Santos 算法在计算凹壳时，速度通常比 PCL 的 alpha-shape 快。我没有试图优化 PCL 代码的速度，也许有更多 PCL 经验可以获得更好的性能。

就像这个算法一样，alpha-shape 计算也是一种迭代解决方案，其中初始的 α 猜测反复增加或减少，直到找到一个多边形，这就是凹壳。因此，两者之间的公平比较应该只对两者进行一次迭代。即，最终的 K 值与最终的 α 值。这就是我在上述三个大型示例中所示意的：