65.9K
CodeProject 正在变化。 阅读更多。
Home

使用 GO 语言解决三角形问题

José Cintra
starIconstarIconstarIconstarIcon
emptyStarIcon
starIcon

4.28/5 (6投票s)

2018 年 12 月 10 日

CPOL

5分钟阅读

viewsIcon

11740

downloadIcon

92

GO 包封装数据和方法，用于计算三角形的主要度量

引言

解决三角形意味着找到缺失的边、角和其他度量。计算的形式将取决于您已经知道的边或角。
我们将使用的方法适用于我们知道三角形三边度量（SSS）的情况。
为此，我们将用GO 语言创建一个包含所有结构和方法的包来执行计算。

背景

请看下面的通用三角形 ABC

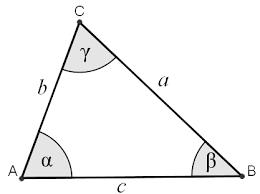
根据其边a、b 和 c的度量信息，我们可以计算以下元素

  1. 周长 ⇒ A 周长是环绕二维形状的路径。在三角形的情况下，它是其边之和

  2. 半周长 ⇒ 半周长（S）定义为周长长度的一半

  3. 面积 ⇒ 三角形的面积可以通过海伦公式（有时称为海伦公式）获得

  4. 角度 ⇒ 我们可以使用余弦定律来计算三角形的角度：

  5. 高 ⇒ 三角形的高是相对于特定边（底）的最高高程。因此，每个三角形都有三个高（Ha、Hb 和 Hc），可以通过其面积轻松计算

  6. 中线 ⇒ 中线是从顶点连接到对边中点的线段。

    每个三角形都有 3 条中线。以下是计算中线（ma、mb 和 mc）长度的公式：

  7. 内切圆和外切圆 ⇒ 每个三角形都可以内接和外接一个圆。要计算这些圆的半径测量值（InRadius (Ri) 和 CincumRadius (Rc)），我们使用以下公式

  8. 三角形的类型 ⇒ 三角形根据其元素的相对大小进行分类。

    就其边而言，三角形可以是

    • 不等边三角形（所有边都不同）
    • 等腰三角形（两条边相等）
    • 等边三角形（三条边都相等）

    就其角度而言，三角形可以是

    • 锐角三角形（所有角都是锐角）
    • 直角三角形（一个角是直角）
    • 钝角三角形（一个角是钝角）

Using the Code

GO 语言在名称、格式和文件位置方面非常严格。
源代码文件应组织到包中，这些包应放置在名为 src 的父文件夹下，这是我们的工作区文件夹。

为了更好地理解，还应注意其他重要事项

  • 包名必须小写。
  • 必须在操作系统中设置以下环境变量
    • GOPATH ⇒工作区文件夹地址
    • GOROOT ⇒如果您选择的目录不是 c:\Go，则必须将 GOROOT 环境变量设置为您选择的路径。
    • PATH ⇒将 Go 根目录的 bin 子目录（例如，c:\Go\bin）添加到您的 PATH 环境变量。

对于本文，我们创建了以下文件

Triangle.go ⇒ 三角形的表示，包含必要的结构和方法。此文件将保留在文件夹：go/src/math/geometry/polygon

TriangleTest.go ⇒ 使用 polygon 包的示例，我们在其中创建了一个三角形并执行了一些计算测试。此文件将保留在文件夹：go/src/math/geometry

让我们来看看 GO 代码……

Triangle.go

/*

Triangle.go
Calculations with triangles

Language: GO

2018, Jose Cintra
email: josecintra@josecintra.com

*/

package polygon

import "math"

type Triangle struct {
	a          float64 // Size of A Side
	b          float64 // Size of B Side
	c          float64 // Size of C Side
	isTriangle bool    // These sides are valid for a triangle?
}

// Getter for the sides of the triangle
func (self Triangle) Sides() (float64, float64, float64) {
	return self.a, self.b, self.c
}

// Setter for the sides of the triangle
func (self *Triangle) SetSides(a, b, c float64) bool {
	self.isTriangle = false
	self.a = a
	self.b = b
	self.c = c
	if self.a <= (self.b+self.c) && self.b <= (self.a+self.c) && self.c <= (self.a+self.b) {
		self.isTriangle = true
	}
	return self.isTriangle
}

// These sides are valid for a triangle? (Getter)
func (self Triangle) IsTriangle() bool {
	return self.isTriangle
}

// Calculates the perimeter
func (self Triangle) Perimeter() float64 {
	perimeter := 0.0
	if self.IsTriangle() {
		perimeter = (self.a + self.b + self.c)
	}
	return perimeter
}

// Calculates the semiperimeter
func (self Triangle) Semiperimeter() float64 {
	semiperimeter := 0.0
	if self.IsTriangle() {
		semiperimeter = self.Perimeter() / 2
	}
	return semiperimeter
}

// Calculates the area of the triangle through Heron's Formula
func (self Triangle) Area() float64 {
	area := 0.0
	s := self.Semiperimeter()
	if self.IsTriangle() {
		area = math.Sqrt(s * ((s - self.a) * (s - self.b) * (s - self.c)))
	}
	return area
}

// Calculates the radius of the inscribed circle
func (self Triangle) InRadius() float64 {
	inRadius := 0.0
	semiperimeter := self.Semiperimeter()
	area := self.Area()
	if self.IsTriangle() {
		inRadius = area / semiperimeter
	}
	return inRadius
}

// Calculates the radius of the circumscribed circle
func (self Triangle) CircumRadius() float64 {
	circumRadius := 0.0
	alpha, _, _ := self.Angles()
	if self.IsTriangle() {
		circumRadius = self.a / (2.0 * math.Abs(math.Sin(rad2deg(alpha))))
	}
	return circumRadius
}

// Gets the triangle type according to its sides
func (self Triangle) TypeBySide() string {
	bySide := "None"
	if self.IsTriangle() {
		if self.a == self.b && self.b == self.c {
			bySide = "Equilateral"
		} else if self.a == self.b || self.b == self.c || self.a == self.c {
			bySide = "Isosceles"
		} else {
			bySide = "Scalene"
		}
	}
	return bySide
}

// Gets the type of the triangle according to its angles
func (self Triangle) TypeByAngle() string {
	alpha, beta, gamma := self.Angles()
	byAngle := "None"
	if self.IsTriangle() {
		if alpha == 90 || beta == 90 || gamma == 90 {
			byAngle = "Right"
		} else if alpha > 90 || beta > 90 || gamma > 90 {
			byAngle = "Obtuse"
		} else {
			byAngle = "Acute"
		}
	}
	return byAngle
}

// Calculates the angles of the triangle through the law of cosines
func (self Triangle) Angles() (float64, float64, float64) {
	alpha := 0.0
	beta := 0.0
	gamma := 0.0
	if self.IsTriangle() {
		alpha = math.Acos((math.Pow(self.b, 2.0) + math.Pow(self.c, 2.0) 
		- math.Pow(self.a, 2.0)) / (2.0 * self.b * self.c))
		beta = math.Acos((math.Pow(self.c, 2.0) + math.Pow(self.a, 2.0) 
		- math.Pow(self.b, 2.0)) / (2.0 * self.c * self.a))
		gamma = math.Acos((math.Pow(self.b, 2.0) + math.Pow(self.a, 2.0) 
		- math.Pow(self.c, 2.0)) / (2.0 * self.a * self.b))
	}
	alpha = rad2deg(alpha)
	beta = rad2deg(beta)
	gamma = 180 - (alpha + beta)
	return alpha, beta, gamma
}

// Calculates the heights of the triangle using the area formula
func (self Triangle) Heights() (float64, float64, float64) {
	area := self.Area()
	aHeight := 0.0
	bHeight := 0.0
	cHeight := 0.0
	if self.IsTriangle() {
		aHeight = 2.0 * area / self.a
		bHeight = 2.0 * area / self.b
		cHeight = 2.0 * area / self.c
	}
	return aHeight, bHeight, cHeight
}

// Calculates the Medians of the triangle
func (self Triangle) Medians() (float64, float64, float64) {
	aMedian := 0.0
	bMedian := 0.0
	cMedian := 0.0
	if self.IsTriangle() {
		aMedian = math.Sqrt(2.0*math.Pow(self.b, 2.0)+
		2.0*math.Pow(self.c, 2.0)-math.Pow(self.a, 2.0)) / 2.0
		bMedian = math.Sqrt(2.0*math.Pow(self.a, 2.0)+
		2.0*math.Pow(self.c, 2.0)-math.Pow(self.b, 2.0)) / 2.0
		cMedian = math.Sqrt(2.0*math.Pow(self.a, 2.0)+
		2.0*math.Pow(self.b, 2.0)-math.Pow(self.c, 2.0)) / 2.0
	}
	return aMedian, bMedian, cMedian
}

// Convert from radians to degree
func rad2deg(rad float64) float64 {
	return rad * 180 / math.Pi
}

TriangleTest.go

/*
TriangleTest
Test for the Triangle Package

Language: GO

2018, Jose Cintra
email: josecintra@josecintra.com
*/

package main

import (
	"fmt"
	"math/geometry/polygon"
)

func main() {
	fmt.Printf("\nTriangle Calculations\n\n")
	// Data entry
	var a, b, c float64
	fmt.Printf("Enter the size of the a side: ")
	fmt.Scan(&a)
	fmt.Printf("Enter the size of the b side: ")
	fmt.Scan(&b)
	fmt.Printf("Enter the size of the c side: ")
	fmt.Scan(&c)

	// Triangle object
	tri := new(polygon.Triangle)
	tri.SetSides(a, b, c)

	// Print the calculations
	fmt.Printf("\nResults:\n")
	if tri.IsTriangle() {
		fmt.Printf("Type by side = %s\n", tri.TypeBySide())
		fmt.Printf("Type by angle = %s\n", tri.TypeByAngle())
		fmt.Printf("Perimeter = %f\n", tri.Perimeter())
		fmt.Printf("Semiperimeter = %f\n", tri.Semiperimeter())
		fmt.Printf("Area = %f\n", tri.Area())
		fmt.Printf("Radius of the circumscribed circle = %f\n", tri.CircumRadius())
		fmt.Printf("Radius of the inscribed circle = %f\n", tri.InRadius())
		alfa, beta, gama := tri.Angles()
		fmt.Printf("Alfa, Beta, Gama Angles = %f, %f, %f \n", alfa, beta, gama)
		fmt.Printf("Sum of the Angles = %f \n", (alfa + beta + gama))
		aHeight, bHeight, cHeight := tri.Heights()
		fmt.Printf("Heights a, b and c = %f, %f, %f \n", aHeight, bHeight, cHeight)
		aMedian, bMedian, cMedian := tri.Medians()
		fmt.Printf("Medians a, b and c = %f, %f, %f \n", aMedian, bMedian, cMedian)
	} else {
		fmt.Printf("These sides do not form a triangle!\n\n")
	}
}

关注点

左键单击 gadget 并拖动以移动它。左键单击 gadget 的右下角并拖动以调整其大小。右键单击 gadget 以访问其属性。

  • 首字母大写的变量名和方法具有全局可见性（public）；
  • 首字母小写的变量名和方法具有局部可见性（private）；
  • 就像在 Lua 语言中一样，GO 中的函数可以返回多个值。这在数学上不正确，但非常实用。在大多数情况下，此功能用于返回错误代码，这很棒。

Triangle.go

  • Go 没有按引用传递的函数调用语义。相反，我们在需要时使用按指针传递，例如在 SetSides 方法中；
  • 在 Go 中，没有类或构造函数。相反，我们使用结构类型和 Setter 方法；
  • Triangle 结构有四个变量
    • 三个浮点变量（a、b、c）用于表示三角形的边长。
    • 一个布尔变量（isTriangle），指示这三条边是否有效构成一个三角形。

      请注意，这些变量以小写字母开头，这意味着它们具有局部可见性范围。为了让外部例程访问这些变量，有访问器方法 Sides（Getter）和 SetSides（Setter）。
      所有方法在执行计算之前都会测试此变量。

  • SetSides 方法通过使用解引用运算符按引用接收参数。
  • rad2deg 函数是一个私有方法，因此无法从外部访问。

TriangleTest.go

  • “main”包中的 main 函数将是我们可执行程序的入口点。
  • 在 main 方法中，我们使用 new，这是一个内置函数，用于为 Triangle 类型分配内存并返回其地址。

关于精度的说明

涉及浮点值的计算不准确。根据我们的测试，GO 中的 float64 类型非常精确，但即便如此，也应采取一些措施。
例如，在角度计算中，我们使用了一个技巧来确保其总和始终为 180 度。

此外，一些罕见的三角形类型可能会产生意外结果。它们是

  • 一个退化三角形，一个顶点共线且面积为零的三角形。这种情况将在我们的算法中导致一个无效的三角形，并且计算将不会执行；
  • 一个针状三角形，一个三角形的两条边之和略大于第三条边（几乎是一条直线段）。在这种情况下，我们的计算可能会导致精度错误。

后续步骤

未来可以进行的一些增强

  • 允许不仅通过其边（SSS）计算三角形，还可以通过其他组合来计算
  • 创建一个多边形接口来执行与其他几何形状的计算
  • 通过预测针状三角形的情况来改进计算

了解更多……

三角形

GO 语言

历史

  • 2018-12-11 - 添加了精度部分

结束语

感谢阅读！
在 GitHub 上找到我，获取更多数学算法。

© . All rights reserved.