强化学习 - 一个井字棋示例
5.00/5 (3投票s)
一个关于如何使用时间差分算法在不到一分钟的时间内教会机器在井字棋游戏中变得无敌的示例。
引言
强化学习是一个循序渐进的机器学习过程,在每一步之后,机器都会收到一个奖励,该奖励反映了该步骤在实现目标方面的优劣。通过探索其环境并利用最有益的步骤,它学会了在每个阶段选择最佳行动。
井字棋示例
本文旨在教人工智能玩井字棋,或者更准确地说,是赢得井字棋。它实际上并不知道游戏规则,也不会存储已采取的走法的历史记录。在每个回合,它只是从可用的走法中选择一个具有最高潜在奖励的走法。这些走法的相对价值是在训练过程中,通过模拟游戏中的走法和接收到的奖励来学习的。在深入了解如何实现这一点之前,有必要澄清一些在强化学习中使用的术语。
强化学习术语
人工智能被称为Agent(智能体)。在每一步,它都会执行一个Action(动作),该动作会导致其操作的Environment(环境)的state(状态)发生变化。环境会根据动作的好坏来奖励智能体。然后,环境会向智能体提供反馈,反映环境的新状态,并使智能体能够获得足够的信息来采取下一步行动。智能体遵循一个policy(策略),该策略决定了它在给定状态下采取的动作。学习过程会改进策略。因此,实际上正在构建的是策略,而不是智能体。智能体是策略的代理,执行策略指定的动作。每个状态都有一个预期的回报值(以奖励衡量)。状态的值用于在状态之间进行选择。策略通常是贪婪的。也就是说,选择具有最高值的状态,因为强化学习的基本前提是,在每一步都产生最高预期奖励的策略是最佳策略。为了使此决策过程能够正常工作,该过程必须是一个马尔可夫决策过程。
马尔可夫决策过程
马尔可夫决策过程(MDP)是一个循序渐进的过程,其中当前状态包含足够的信息,能够确定处于每个后续状态的概率。为了更好地理解 MDP,有时最好考虑什么过程不是 MDP。如果您试图在给定时间步长绘制汽车的位置,并且您知道方向但不知道汽车的速度,那么这就不可能是 MDP,因为无法确定汽车在每个时间步长的位置(状态)。另一个例子是这样一个过程:在每一步,动作是从一副牌中抽出一张牌,如果是人头牌则向左移动,如果不是则向右移动。在这种情况下,可能的下一个状态是已知的,即左边的状态或右边的状态,但是处于任一状态的概率是未知的,因为不知道牌在牌堆中的分布,所以它不是 MDP。
将井字棋实现为马尔可夫决策过程
井字棋很容易实现为马尔可夫决策过程,因为每一步都是一个改变游戏状态的动作。智能体在每一步可用的动作数量等于棋盘3x3网格上未被占用的方格数量。智能体需要能够查找每种可用动作导致的状态(以预期奖励衡量)的值,然后选择具有最高值的动作。智能体在训练过程中学习状态和动作的值,此时它会采样许多走法以及因此获得的奖励。作为训练过程的一部分,会记录一个状态值更新的次数,因为每次更新时,值的更新量都会减少。因此,每个状态都需要一个唯一的键,该键可用于查找该状态的值以及该状态已被更新的次数。如果可以将游戏状态加密为数值,则它可以作为字典的键,该字典存储状态已更新的次数以及状态本身的值,类型为ValueTuple,类型为int,double。最直接的方法是将状态编码为最多九位数的正整数,其中“X”的值为2,“O”的值为1。因此,下面的游戏状态将被编码为200012101。
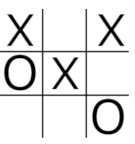
一个方格中的“X”的值等于2乘以10的方格索引值(0-8)的幂;但使用基数3而不是基数10更有效,因此,使用基数3表示法,棋盘编码为
(1*3^0)+(1*3^2)+(2*3^3)+(1*3^4)+(2*3^8)=13267
将棋盘数组加密为基数3数字的方法非常直接。
public int BoardToState()
{
int id = 0;
for (int i = 0; i < Squares.Length; i++)
{
int value = 0;
if (!Squares[i].IsEmpty)
{
value = Squares[i].Content == 'X' ? 1 : 2;
id += (int)(value * Math.Pow(3, Squares[i].BoardIndex));
}
}
return id;
}
解密方法如下:
public IBoard StateToBoard(int s)
{
int state = s;
var board = new OXBoard();
for (int i = board.Squares.Length-1; i >=0; i--)
{
int value =(int)(state/ Math.Pow(3, i));
if(value!=0)
{
board[i].Content = value == 1 ? 'X' : 'O';
state -= (int)(value * Math.Pow(3, i));
}
}
return board;
}
下面的StateToStatePrimes方法会遍历空方格,并在每次迭代时,选择如果智能体占据该方格将导致的新状态。然后将选定的状态作为数组返回,智能体可以从中选择具有最高值并执行其走法的状态。
public int[] StateToStatePrimes(int state)
{
int existingState = state;
List<int> statePrimes = new List<int>();
for (int i = 8; i >= 0; i--)
{
int value = (int)(state / Math.Pow(3, i));
if (value == 0)
{
//agent is'O'
var sPrime = existingState + (int)(2 * Math.Pow(3, i));
statePrimes.Add(sPrime);
}
state -= (int)(value * Math.Pow(3, i));
}
return statePrimes.ToArray();
}
有了这些方法,接下来要考虑的是如何学习一个策略,其中分配给状态的值是准确的,并且执行的动作是获胜的动作。这时贝尔曼方程就派上用场了。
贝尔曼方程
强化学习围绕贝尔曼方程展开。该方程将当前状态的值与后续每一步动作的预期奖励联系起来。它包含两部分:采取动作的奖励以及下一个状态的折扣值。
v(s1) = R + γ*v(s2)
其中 v(s1) 是当前状态的值,R 是采取下一个动作的奖励,γ*v(s2) 是下一个状态的折扣值。Gamma (γ) 是折扣因子。它的使用使得即时奖励比未来奖励更重要。折扣因子在连续过程中特别有用,因为它可以防止无限循环导致奖励无限增加。贝尔曼方程在每一步都使用,并以类似递归的方式应用,以便下一个状态的值在采取下一步时成为当前状态的值。因此,确定初始状态值的问题被分解为通过一系列步骤应用贝尔曼方程,直到最终走法。实际上,从结束游戏的走法开始反向思考更容易。这正是动态规划中使用的处理方法。
动态编程
动态规划不像 C# 编程。它是一种通过将数学问题分解为一系列步骤来解决问题的方法。通过反复应用贝尔曼方程,可以通过从每个可能的最终状态(最后一步)向后(回溯)到所有初始状态(初始走法),来确定井字棋中每个可能状态的值。为了了解其工作原理,请考虑以下示例。
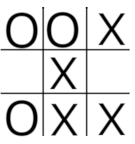
奖励系统设定为获胜 11 分,平局 6 分。智能体playerO处于状态 10304,它有两种动作选择:移动到第 3 格,这将导致转换到状态 10304 + 2*3^3=10358 并赢得比赛,奖励为 11;或者移动到第 5 格,这将导致转换到状态 10304 + 2*3^5=10790,在这种情况下比赛是平局,智能体获得 6 分奖励。策略选择具有最高奖励的状态,因此智能体移动到第 3 格并获胜。通过这次经历,智能体可以获得重要信息,即处于状态 10304 的价值。从这个状态开始,它有均等的选择,可以移动到状态 10358 并获得 11 分奖励,或者移动到状态 10790 并获得 6 分奖励。因此,处于状态 10304 的价值是 (11+6)/2=8.5。状态 10358 和 10780 被称为终端状态,其价值为零,因为状态的价值被定义为从该状态开始并遵循智能体策略所产生的预期回报的价值。通过考虑所有可能的最终走法并不断地将状态值从当前状态回溯到前一步所有可用的状态,就有可能确定所有相关的值,一直回溯到初始走法。这在井字棋这样简单的游戏中是可行的,但在大多数情况下计算成本太高。更实用的方法是使用蒙特卡洛评估。
蒙特卡洛评估
蒙特卡洛评估通过反复采样 MDP 的完整回合,并确定许多回合中遇到的每个状态的平均值,来简化确定 MDP 中每个状态值的过程。在井字棋中,一个回合是一场完整的比赛。如果在第一个回合中,结果是获胜且奖励值为 10,则游戏中遇到的每个状态的值都将为 10。如果在第二个回合中,结果是平局且奖励为 6,则游戏中遇到的每个状态的值都将为 6,但对于也出现在第一个回合中的状态除外。这些状态现在的值将为 (10+6)/2=8。经过许多回合,状态的值将非常接近其真实值。对于井字棋游戏,此技术效果很好,因为 MDP 过程较短。但是,当将其应用于更复杂的 MDP 时,会出现几个问题。状态值需要很长时间才能收敛到其真实值,并且必须等待每个回合结束才能进行任何学习。还有其他可用的技术可以确定最佳策略,并且可以避免这些问题,其中一个著名的是时间差学习。
时间差学习
时间差学习是一种算法,通过反复采样从状态到状态的转移来改进每一步动作选择的策略。它通过采用一种称为引导(bootstrapping)的机制来更新状态值,从而在性能上优于蒙特卡洛评估。引导是通过使用下一个状态的值来“拉动”(提高或降低)现有状态的值来实现的。由于它是一步前瞻,因此可以在 MDP 实际运行时使用,而无需等到过程结束。学习过程涉及使用在某个状态下采取的动作的值来更新该状态的值。状态的值被正式定义为从该状态开始并遵循智能体策略所产生的预期回报的价值。动作的值是从采取该动作并遵循智能体策略开始的预期奖励的价值。为了从动作值更新状态值,需要知道动作导致转移到下一个状态的概率。并非总是有 100% 的概率,因为某些动作包含随机成分。但是,如果存储动作值而不是状态值,则可以通过从动作值到动作值进行采样来更新其值,这类似于蒙特卡洛评估,并且智能体不需要具有转换概率模型。使用动作值而不是状态值的时间差学习称为 Q-Learning(Q 值是动作值的另一个名称)。贝尔曼方程用于更新动作值。
currentStateVal = currentStateVal + alpha * (-1 + (gamma*newStateVal) - currentStateVal);
当前状态的 Q 值将被更新为当前状态的 Q 值加上下一个状态的 Q 值减去当前状态的值乘以一个因子“alpha”。下一个状态的值包括移动到该状态的奖励(-1)。变量 alpha 是应用于两个状态之间差值的折扣因子。状态更新的次数越多,更新量就越小。Alpha 简单地等于 1/N,其中 N 是状态更新的次数。如前所述,γ 是用于折扣未来奖励的折扣因子。使用 Epsilon 贪婪策略来选择动作。
Epsilon 贪婪策略改进
贪婪策略是在每个时间步长选择具有最高 Q 值的动作的策略。如果将其应用于每一步,将导致对 MDP 中现有路径的过度利用,而对新路径的探索不足。因此,在每一步,以 epsilon 的频率进行随机选择,并以 1-epsilon 的频率选择贪婪策略。在短 MDP 中,epsilon 最好设置为较高的百分比。在广泛的 MDP 中,epsilon 可以设置为较高的初始值,然后随着时间的推移而降低。
学习方法
每个状态需要存储两个值:状态的值以及值已更新的次数。使用Dictionary来存储所需数据。它使用编码为整数的状态作为键,并使用类型为int, double的ValueTuple作为值。键引用状态,ValueTuple存储更新次数和状态的值。
public Dictionary<int, (int, double)> FitnessDict { get; private set; }
//.....
public void Learn(int[] states, GameState gameState)
{
double gamma = Constants.Gamma;
int currState = states[0];
int newState = states[1];
UpdateFitnessDict(newState, gameState);//add if not present
(int currStateCount, double currStateVal) = FitnessDict[currState];
currStateCount += 1;
double alpha = 1 / (double)currStateCount;
(int newStateCount, double newStateVal) = FitnessDict[newState];
if (gameState != GameState.InPlay)
{
currStateVal = currStateVal + (alpha * (rewardsDict[gameState] - currStateVal));
FitnessDict[currState] = (currStateCount, currStateVal);
return;
}
currStateVal = currStateVal + alpha * (-1 + (gamma*newStateVal) - currStateVal);
FitnessDict[currState] = (currStateCount, currStateVal);
}
private void UpdateFitnessDict(int newState, GameState gameState)
{
if (!FitnessDict.ContainsKey(newState))
{
FitnessDict.Add(newState, (0, rewardsDict[gameState]));
}
}
培训
训练包括反复从状态到状态采样动作,并在每个动作后调用学习方法。在训练期间,游戏中的每一步都是 MDP 的一部分。在智能体的走法时,智能体有动作选择,除非只剩一个空方格。当轮到对手走法时,智能体移动到一个由对手选择的状态。这种安排使智能体能够从自己的选择和对手的反应中学习。它还封装了每一次状态的变化。训练需要包括智能体先走的游戏和对手先走的游戏。训练方法异步运行,并支持进度报告和取消。
public void Train(int max, bool isOFirst, IProgress<int> progress, CancellationToken ct)
{
int maxGames = max;
int[] states = new int[2];
char[] Players = isOFirst ? new char[] { 'O', 'X' } : new char[] { 'X', 'O' };
int totalMoves = 0;
int totalGames = 0;
Move move;
while (totalGames < maxGames)
{
move.MoveResult = GameState.InPlay;
move.Index = -1;
int moveNumber = 0;
int currentState = 0;
int newState = 0;
board.Reset();
while (move.MoveResult == GameState.InPlay)
{
char player = Players[moveNumber % 2];
move = player == 'X' ? RandMoveX() : RandMoveO(currentState);
board[move.Index].Content = player;
newState = board.BoardToState();
if (move.MoveResult == GameState.InPlay
&& !board.Lines.Any(l => !l.IsLineOblocked || !l.IsLineXblocked))
{
move.MoveResult = GameState.Draw;
}
states[0] = currentState;
states[1] = newState;
learner.Learn(states, move.MoveResult);
currentState = newState;
moveNumber++;
}
totalMoves += moveNumber - 1;
totalGames += 1;
if(totalGames % Constants.ReportingFreq == 0)
{
progress.Report(totalGames / maxGames);
ct.ThrowIfCancellationRequested();
}
}
}
无懈可击测试
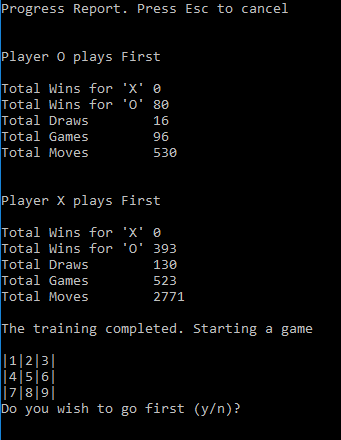
训练周期包括两个部分。第一部分,智能体进行初始走法。第二部分,对手开始游戏。在每个部分之后,都会测试策略对抗对手的所有可能的走法。当对手没有找到获胜的方法时,训练停止,否则重复该周期。在我的机器上,训练通常不到一分钟即可完成。关于测试方法以及确定各种游戏状态的方法的详细信息,请参见一篇较早的文章,其中开发了一种基于策略的井字棋玩法解决方案。
private Progress<int> progress = new Progress<int>();
private CancellationTokenSource cts = new CancellationTokenSource();
private IRandomTrainer trainer;
private IInfallibilityTester tester;
public TrainingScheduler(IRandomTrainer trainer, IInfallibilityTester tester)
{
this.tester = tester;
this.trainer = trainer;
progress.ProgressChanged += ReportProgress;
}
private void ReportProgress(object sender, int percent)
{
if (Console.KeyAvailable && Console.ReadKey(true).Key == ConsoleKey.Escape)
{
Console.Write(Constants.Cancelling);
cts.Cancel();
}
Console.Write(".");
}
public async Task ScheduleTraining()
{
int runsX = Constants.TrainingRunsX;
int runsO = Constants.TrainingRunsO;
int xFirstResult = -1;
int oFirstResult = -1;
bool isPlayerOFirst = true;
Console.WriteLine(Constants.TrainingPressEsc);
int iterations = 0;
while (xFirstResult != 0 || oFirstResult != 0)//number of'X' wins
{
if (iterations == Constants.IterationsBeforeReset)
{
iterations = 0;
//Resetting the state values and visit counts is not essential
//But it improves efficiency where convergence is slow.
trainer.Reset();
}
try
{
await Task.Run(() => trainer.Train(runsO, isPlayerOFirst, progress, cts.Token));
await Task.Run(() => trainer.Train(runsX, !isPlayerOFirst, progress, cts.Token));
oFirstResult = tester.RunTester(isPlayerOFirst);
xFirstResult = tester.RunTester(!isPlayerOFirst);
iterations += 1;
}
catch (OperationCanceledException)
{
throw;
}
}
}
设置奖励值
让 MDP 中的每一步对智能体来说都“痛苦”很重要,这样它才能走最快的路线。值为 -1 效果很好,并构成了其他奖励的基准。获胜奖励和平局奖励之间必须存在正向差值,否则智能体将选择快速平局而不是缓慢获胜。具体值并不关键。看起来,当Win(10)、Draw(2)和Lose(-30)之间的差异相对较小时,状态值会更快地收敛到其真实值,这可能是因为时间差学习引导了状态值,如果差异很小,则需要的工作量就较少。括号中的数字是示例应用程序中使用的值,此外,折扣值“gamma”设置为 0.9。毫无疑问,如果对这些数字进行一些“微调”,性能可以进一步提高。
结论
强化学习是一种极其强大的算法,它使用一系列相对简单的步骤组合在一起,产生一种人工智能。但是,强化学习中使用的术语以及贝尔曼方程的半递归应用方式可能会让新手难以理解。希望这篇过于简化的文章能在一定程度上揭开该主题的神秘面纱,并鼓励人们进一步研究这个迷人的主题。
参考和致谢
- Tom M. Mitchell 的《机器学习》。对机器学习的概述,其中包含一章关于强化学习的出色内容。
- Richard S. Sutton 和 Andrew G. Barto 的《强化学习:导论》。这是强化学习的权威著作,但对于初学者来说,学习曲线非常陡峭。曾有草稿版本在线可用,但现在可能受版权保护。
- David Silver 的《强化学习课程》。一系列信息量非常大的讲座,假设对该主题一无所知,但对数学符号的理解有所帮助。可在这里免费在线获取。
- Christ Kennedy 的《井字棋 - 无递归的 Minimax》。一种有趣的井字棋暴力破解实现,对如何将游戏状态编码为正的基数 3 整数进行了很好的解释。
