游戏中的声音 - 房间

• 下载 WpfReverberationTime-noexe.zip - 64 KB
• 下载 WpfReverberationTime.zip - 403.9 KB 

介绍  

如今，大多数动作类游戏都会实现某种算法来计算声音在房间、隧道或其他封闭空间中的反射。有几种方法可以实现这种房间内声音的变化，但在此我将展示几种最简单的方法，使用经典理论来展示声学工程师如何看待房间。

房间内的声音模拟非常重要，因为我们听到的声音会让我们对所处的空间做出很多假设。为了逼真地重现声音，我们需要对声压进行一些修改，而这正是声学发挥作用的地方。 

本文后面的程序将计算一个矩形房间的混响时间，您可以在其中选择表面元素。   

混响   

我将通过以下方式解释混响：如果您站在山谷中向一座表面相当平坦的山喊叫，您会听到回声，因为声音会从您的嘴传播到平坦的墙壁，然后反射回您的耳朵。您在房间里听不到回声的原因是天花板、地板和墙壁的反射靠得太近了，以至于您认为回声是声音的一部分。乐器中也存在这种情况，例如吉他、钢琴、鼓等等，即使您停止了琴弦的振动，它们也会在音调发出后很长一段时间内发出声音。 

第一位考虑混响时间的是美国物理学家 W. C. Sabine，他在 1900 年的文章中概述了下面这个通用方程的结果（其中 w 是声源能量，V 是体积，W_abs 是房间内的吸收量）。

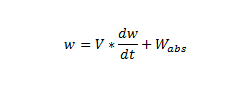
与所有方程一样，它一开始看起来相当困难，但这个方程实际上非常简单。它只是表示，我们声源（扬声器、汽车声音或房间内任何发声体）的能量等于均匀分布在房间内的瞬时能量，加上从我们表面吸收的能量（来自墙壁、天花板或地板的减弱的回声）。吸收实际上是声音从一次反射开始的百分比衰减（类似于光的斯涅尔反射定律，但吸收描述的是反射波中的能量损失），通常表示为 0-1.0 之间的因子。公式中最重要的一点是，根据 Sabine 的方程，房间内的声能处处相等。  

我们将跳过将方程推导为可用的方程的许多细节。总的来说，我们假设所有到达墙壁的声能都以平面波的形式传播，并且通过此假设转换通用方程，可以在任何给定时间给出 p² 值。结果是下面的方程（其中 rho₀ 是空气的密度，在此情况下为 (1.21 kg/m³)，C₀ 是空气中的声速 (343 m/s)，A = 表面积*吸收系数，V 是房间的体积，t 是时间。这适用于文章中给出的所有公式）。

Sabine 公式中的吸收面积根据以下方程计算（其中 S 是表面积，α 是材料的吸收系数）：  

A = S₁ α₁ + S₂ α₂ + ... + S_n α_n = ∑ S_iα_i

可以从这个方程推断出混响时间。如果我们设置一个持续提供已知效应的声源，然后在 t=0 时将其关闭（即 w = 0），我们可以像这样计算声源关闭后的声压。

然而，正如 Sabine 所定义的混响时间，我们只关心声场衰减 60 dB 所需的时间，这实际上与声源无关。因此，混响时间的公式可以设置为如下。

毫不奇怪，这个微分方程可以使用数字 e 来求解。在文章中，这个数字出现在许多解中，因为数字 e^x 是它自身的导数和积分，这可以通过下面使用从 0 到 x 的非有界积分的简单公式来证明（尽管我从未见过这样写）：   

不久之后，理论得到了许多修改，Eyring-Norris（尽管 Schuster 和 Waetzmann 独立发现了这个结果）基于声音波在撞击墙壁之前会有一个平均传播距离的观念。这意味着以射线形式传播的波在反射之间平均会传播一段距离。这很容易解释。如果您在任何墙壁、天花板或地板上的任意点放置一个激光，并以随机方向射出多条射线，激光撞击表面的平均长度就是房间内的平均距离。然而，在房间声学中，我们更感兴趣的是每秒的反射次数，这可以通过下面的公式找到，其中 c 是声速，L_n 是矩形房间的 x、y 和 z 方向的长度，V 是房间的总体积（两个不同的公式使用不同的技术导出，但它们产生相同的结果）。

有了这些信息，我们就可以轻松找到每单位时间反射的次数，从而得到混响场衰减率的函数。该方程的推导如下（一个小的说明是，下面的公式中 α 是平均吸收系数，可以表示为 a_alpha = A / S*）： 

通过计算墙壁的平均吸收量如下：

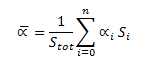
这实际上与 Sabine 的方程非常相似，只是由于入射角而不是平面波，α 稍微大一点。如果我们取吸收函数的级数展开，这一点就更清楚了：  

但 Eyring-Norris 方法的问题在于，入射角在整个房间是漫射的，如果某些表面的吸收系数差异很大，这可能会成为一个问题。因此，Millington-Sette 进行了修改，您可以使用 Eyring-Norris 公式并将其应用于较小的区域。Millington-Sette 给出了以下表达式：

有一个简单的衰减系数公式，适用于 1.5 到 10 kHz 之间，其中 h 是相对湿度（适用于 20-70%），i 是百分比，f 是频率。近似公式如下：   

空气衰减的精确公式在 ISO 9613-2 中给出，您可以在这里查看。

它们与混响公式结合在一起，因为空气衰减只是另一个吸收系数。由此得到的 Sabine 的修改方程为：  

Eyring-Norris：  

Millington-Sette

这些混响公式的问题在于它们并不完全正确。当您看到推导它们所基于的假设类型时，您就会明白为什么。主要问题之一是房间中的所有方向都可能存在驻波，这会导致感知到的混响时间与您通过上述三个公式之一计算出的混响时间不同。一种尝试解决这种情况的方法是 Frizroy 的方程，该方程基于计算不同方向的混响时间并取平均值。他提出的公式如下：  

考虑空气吸收的近似公式（如果您进行计算，就会发现它不准确，但通常也不算太差）： 

近年来，出现了一些其他公式（此处未给出），它们也试图捕捉不同方向的混响时间。但除非您考虑散射，否则您将无法获得正确的混响时间曲线。您可以观看视频，其中 Jens Holger Rindel（声学软件 Odeon 的开发者之一）很好地解释了其中一些内容。

他解释了，在某些房间中，对指数衰减取对数后，衰减率可能不是一条直线。在某些情况下，您可能会得到指数衰减。这是由于 x、y 和 z 方向上的平行墙壁。如果混响时间变化很大，声能会在吸收率较低的方向上停留更长时间。如果您想象一个平面波朝向墙壁传播，由于散射，一部分能量会在另外两个方向上反射。因此，混响时间曲线将受到具有较低混响时间的方向与具有较高混响时间的方向之间的耦合影响最大，并且这会发生在整个混响时间曲线上，因为方向随着时间的推移会有无限多个耦合的平行墙壁（这类似于耦合房间的问题）。

然而，混响场的计算仅限于测量吸收系数的精度，而吸收系数的差异可能高达 +/- 5%。所以即使我们有完美的混响时间公式，也没有意义。顺便说一句，对于所有物理预测模型来说，情况都是如此，因为它在很大程度上取决于输入的准确性——或者说 GIGO（垃圾进，垃圾出）。

上述所有公式的实现都在下面的代码中给出。

Dim FullOctaveBand() As String
Dim OctaveBandString As String = "31,63,125,250,500,1000,2000,4000,8000,16000"
FullOctaveBand = OctaveBandString.Split(",")

If Not _lstXAbsorbers.Count = 0 And Not _lstYAbsorbers.Count = 0 _
                      And Not _lstZAbsorbers.Count = 0 Then
    TotalSufraceArea = _TotalSurfaceArea

    Humidity = CInt(txtHumidityRoom.Text)

    Sabine.Name = "Sabine"
    Eyring.Name = "Eyring"
    Miller.Name = "Millington-Sette"
    Fritzroy.Name = "Fritzroy"

    Volume = _Height * _Length * _Width

    For i As Integer = 0 To Sabine.Count - 1

        Dim SabineTempZ, SabineTempY, SabineTempX As Double
        SabineTempX = 0
        SabineTempY = 0
        SabineTempZ = 0

        Dim EyringTempZ, EyringTempY, EyringTempX As Double
        EyringTempZ = 0
        EyringTempY = 0
        EyringTempX = 0

        Dim MillingtonSetteTempZ, MillingtonSetteTempY, MillingtonSetteTempX As Double
        MillingtonSetteTempZ = 0
        MillingtonSetteTempY = 0
        MillingtonSetteTempX = 0

        For Each p As Absorber In _lstZAbsorbers
            SabineTempZ += p.Area * p.GetItem(i)
            EyringTempZ += p.Area * p.GetItem(i) / _TotalSurfaceArea
            MillingtonSetteTempZ += p.Area * CalculateAlfa(p.GetItem(i))
        Next

        For Each p As Absorber In _lstYAbsorbers
            SabineTempY += p.Area * p.GetItem(i)
            EyringTempY += p.Area * p.GetItem(i) / _TotalSurfaceArea
            MillingtonSetteTempY += p.Area * CalculateAlfa(p.GetItem(i))
        Next
 
        For Each p As Absorber In _lstXAbsorbers
            SabineTempX += p.Area * p.GetItem(i)
            EyringTempX += p.Area * p.GetItem(i) / _TotalSurfaceArea
            MillingtonSetteTempX += p.Area * CalculateAlfa(p.GetItem(i))
        Next

        Dim m As Double = 5.5 * 10 ^ (-4) * (50 / Humidity) * _
                          (CDbl(FullOctaveBand(i)) / 1000) ^ (1.7)

        'Calculationg total absorbtion area and air annutaion 
        Dim AbsorbtionAreaSabine As Double = (SabineTempX + SabineTempY + SabineTempZ) + 4 * m * Volume
        Dim AbsorbtionAreaEyring As Double = _TotalSurfaceArea * _
            CalculateAlfa(EyringTempX + EyringTempY + EyringTempZ) + 4 * m * Volume
        Dim AbsorbtionAreaMillingtonSette As Double = MillingtonSetteTempX + _
            MillingtonSetteTempY + MillingtonSetteTempZ + 4 * m * Volume


        Dim FritzroyTempZ, FritzroyTempY, FritzroyTempX As Double
        FritzroyTempX = CDbl(lblXrea.Content) / (CalculateAlfa(EyringTempX) + _
           (4 * m * Volume / 3) * (CDbl(lblXrea.Content) / _TotalSurfaceArea ^ 2))
        FritzroyTempY = CDbl(lblYrea.Content) / (CalculateAlfa(EyringTempY) + _
          (4 * m * Volume / 3) * (CDbl(lblYrea.Content) / _TotalSurfaceArea ^ 2))
        FritzroyTempZ = CDbl(lblZarea.Content) / (CalculateAlfa(EyringTempZ) + _
          (4 * m * Volume / 3) * (CDbl(lblZarea.Content) / _TotalSurfaceArea ^ 2))


        Sabine.SetItem(i, ReverberationTime(AbsorbtionAreaSabine))
        Eyring.SetItem(i, ReverberationTime(AbsorbtionAreaEyring))
        Miller.SetItem(i, ReverberationTime(AbsorbtionAreaMillingtonSette))
        Fritzroy.SetItem(i, (0.16 * Volume / (_TotalSurfaceArea ^ 2)) * _
          (FritzroyTempX + FritzroyTempY + FritzroyTempZ))
    Next

    Dim AverageReverberationTimeSabine As Double
    AverageReverberationTimeSabine = 0
    For i As Integer = 0 To Sabine.Count - 1
        AverageReverberationTimeSabine += Sabine.GetItem(i) / Sabine.Count
    Next
 
    'Calculate the Schroeder frequency based on Sabine
    Schroeder = 2000 * Math.Sqrt(AverageReverberationTimeSabine / Volume)

    'Room radius is calculated besed on a omnidirectional source, meaning D = 1
    RoomRadius = Math.Sqrt(55.26 * Volume / (16 * Math.PI * C0 * AverageReverberationTimeSabine))

    lblSchroder.Content = Math.Round(Schroeder, 0).ToString
    lblRoomRadius.Content = Math.Round(RoomRadius, 2).ToString

    _lstResult2.Add(Sabine)
    _lstResult2.Add(Eyring)
    _lstResult2.Add(Miller)
    _lstResult2.Add(Fritzroy)

    lstResult.ItemsSource = _lstResult2

    For Each p As Absorber In _lstResult2
        PlotReverbrationTime(p, False)
    Next

Else
    MessageBox.Show("missing absorbers")
End If

关于公式的注释

关于推导出的结果，特别是理论的局限性，可以给出几点评论。假设房间内的所有点都具有完全相同的能量，这被用来推导出吸收表面在房间内的位置无关紧要。  

实际上有一个简单的电气电路理论类比。房间可以建模为一个简单的电容器，因此房间内的吸收可以看作一个简单的电阻，而狭缝（如窗户、门等）的泄漏可以建模为一个电感器。显然，“正常”房间会表现为具有取决于边界声学特性和房间几何形状的系数的带通滤波器。这意味着我们可以根据电容器上的电荷来模拟房间内的能量： 

 

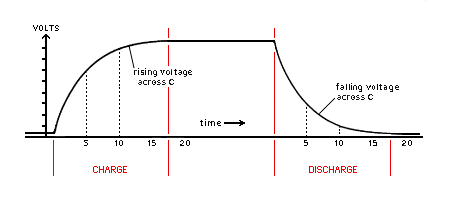
稳态条件可以在电荷和放电之间找到，房间内也一样。在电容器类比中，混响时间计算与电容器的放电相同。然而，电容器的充电也有其在房间声学中的等价物，它被称为早期衰减时间 (EDT)。在电容器和房间之间的类比中，有几点缺失。一是直达声，即听者与声源之间的最短路径；二是声学中的稳态是三种不同现象的组合，即直达声、EDT 和最后的混响时间，而电容器仅由充电和放电组成。并且单电容器中也不存在 3D 耦合墙。因此，下面图片显示了脉冲响应的平方与用不同颜色标记的不同区域的模拟： 

 

在傅里叶分析中，房间节点或特征值常用于声学，以解释声压如何在房间内分布。问题是，在这个假设下，墙壁是声源，这与推导 Sabine 方程中混响时间的假设相同，因此无法在声源任意放置的房间中获得正确的声压值。

它们确实解释了房间内墙壁的影响，通过对房间内多个测量点的平均值进行计算，其中声源和麦克风位置都已改变。这实际上是已知信息，Waterhouse 根据这个假设计算了一个公式，因为低频下的声压由于低频节点的影响而必须固定。

到目前为止，本文仅解释了房间内混响部分的声音情况。直达声在游戏中相对容易实现，因为它是声源和接收器之间直接的或最短的距离。早期反射对于模拟房间内的声场非常重要，因为我们感知到的空间信息大部分在此处被拾取。这部分通常使用镜像源或镜像源进行模拟。通常，最重要的信息来自直达声之后的 0 到 80 毫秒，EDT 在标准中定义为从第一次反射开始的 10 dB 衰减。（在测量中，它定义为从最高点 -0.1 dB 到 -10.1 dB，因为人们试图排除直达声的影响。） 

那么，如果我们无法精确计算声压，可以使用哪些技术呢？事实证明，唯一能够完全准确预测声场的技术是传输线模型 (TLM) 或等效的有限差分时域 (FDTD)，但计算时间直接与频率相关，因此对于实时处理来说，它不是一种可行的技术。

几何声学是房间声学顾问使用的分析工具，这是一种结合了射线和镜像源的混合解决方案。使用的程序示例包括：   

• Odeon 
• Catt 

我知道的只有这两款，可能还有其他提供商业程序的。它们在中高频下可以很好地预测声压，但在低频下则会失败。这是因为在低频下，声音不像射线那样传播，而是更像平面波。射线变换有效的频率可以使用舒尔茨频率来估算。这表明我们的声压何时是漫射的，因此低于此频率，我们可以预期声压会受到边界产生的节点的影响。

然而，在许多情况下，从这些程序中获得的信息对于粗略估计一个听起来可信的衰减曲线来说是过度的。（这并不是说它们不需要，它们是需要的。尤其是在花费数百万美元建造音乐厅、大型演讲厅、剧院、歌剧院等场所，却发现声音破坏了观众/学生的体验时。射线追踪/镜像源技术对于我们听觉最敏感的频率通常也非常可靠。）

声学化     

声学化 (Auralization) 这个名字直接源于可视化 (visualization)，但声音是不可见的，而是可听的，因此得名声学化。然而，它需要大量的处理才能将计算出的混响时间转换为可以用于在房间中人工创造声音的内容。

要创建合理的声音，您需要制作一个 1/3 倍频程带滤波器，该滤波器可以应用于 31.5 Hz - 16000 Hz 的范围（程序仅计算全倍频程带，但值通常可以插值以覆盖 1/3 倍频程带。唯一的例外是不同类型的窄赫姆霍兹吸收器）。这并不容易，需要了解 DSP（数字信号处理）和滤波器设计。房间的伪脉冲响应可以按照以下建议创建： 

1. 获取足够长的白噪声信号（大多数情况下 4 秒或更长应该足够了。（我将假设其值为 1 到 -1，并且我知道 wav 文件中没有这些值）
2. 在所有倍频程带中过滤信号并存储它。
3. 将滤波后的信号乘以 p(t) 方程（或者更准确地说，是 e^-xt 信号）-10 dB。p(t) 可以在不同的混响时间公式中找到。
4. 在开始时添加直达声，值为 1（直达声和混响场之间约 60-80 毫秒的延迟会使其听起来更自然，或者最好使用镜像源计算直达声和混响场之间的声音）。
5. 将您想在游戏中播放的声音（无反射）与提出的滤波器进行卷积。

您现在可能已经猜到了，让游戏听起来自然是一项艰巨的任务，而且我知道有些情况下不建议使用此算法，例如在走廊、户外或其他没有混响场的区域（请查看推导公式时设置的先决条件）。

在使用软件直接使用之前，请注意一点。我不能保证 Excel 文件中提供的吸收系数是正确的，尽管在我看来它们是合理的假设。但同样，您可以添加 Excel 文件中您能想到（或在其他地方找到）的所有项目，所以在这一点上没有问题。

历史 

首次发布 2012 年 7 月 31 日

程序包括

• 混响时间计算（四种不同算法）
• 从可编辑的 Excel 文件加载全倍频程带的吸收数据

参考

我在此列出的书籍提供了对我描述内容的良好解释，如果您想了解更多信息，这些都是很好的参考资料。  

• 《建筑声学》，第一版（2008 年），Tor Erik Vigran，CRC Press 
• 《声学化 - 声学、建模、仿真、算法和声学虚拟现实基础》，第一版（2008 年），Michael Vorlander，Springer。
• 《房间声学》，第五版（2009 年），Henrich Kuttruff，Spon Press。 
• 《声学基础》，第四版，Kinsler、Frey、Coppens 和 Sanders，John Wiley & Sons, Inc. 

有一本书专门介绍材料的反射和吸收，如果您想了解理论计算，绝对应该阅读这本书：  

• 《声学吸声体和扩散体 - 理论、设计和应用》，第二版（2009 年），Trevor J. Cox 和 Peter D'Antonio，Taylor & Francis。   

关于不同混响时间公式的简要历史可以在这里找到：

• http://sound.eti.pg.gda.pl/papers/prediction_of_reverberation_time.pdf

其他一些有趣的网站：

• http://webphysics.davidson.edu/faculty/dmb/py115/ReverbCalc.html  
• http://www.esru.strath.ac.uk/Courseware/Acoustic/aco.htm