65.9K
CodeProject 正在变化。 阅读更多。
Home

Sammon 投影

Günther M. FOIDL
starIconstarIconstarIconstarIcon
emptyStarIcon
starIcon

4.94/5 (32投票s)

2009年10月18日

CDDL

6分钟阅读

viewsIcon

106640

downloadIcon

2171

Sammon 投影是一种非线性投影方法，用于将高维空间映射到低维空间。

引言

探索性数据分析的目标是生成大型数据集的简化描述和摘要。聚类是一种标准方法，另一种替代方法是将高维数据集作为点投影到低维——通常是 2D——显示中。因此，投影的目的是降低数据向量的维度。投影以一种能够尽可能忠实地保留数据项的聚类和度量关系的方式，在较低维空间中表示输入数据项。

Sammon 投影的用途

该投影的主要用途是可视化。Sammon 投影对于所有统计模式识别的初步分析都很有用，因为可以获得类分布的粗略可视化，尤其是类的重叠情况。
我个人主要将其用作数据分析的第一步，然后用自组织映射进行检查。因此，可以“交叉验证”结果。

注意 1：由于投影过程，无法将新的数据项映射到图像中的正确位置，因此必须为每个新数据项重新计算投影。这是因为没有数学方法可以描述新向量的位置。

注意 2：与任何其他统计分析一样，对数据进行归一化可能很有用。一种常见的归一化技术是所谓的 (0,1) 归一化，它对每个属性进行归一化，使其均值为 0，方差为 1。这可以通过减去均值并除以方差来实现。

背景

二维和三维数据可以轻松显示，例如通过散点图。四维数据可以显示为三维散点图，其中点的大小对应于第四维。当涉及到更高维度时，我们必须找到其他解决方案。在这里，我将展示 Sammon 投影，它是一种广泛使用的非线性投影变体，属于度量多维缩放方法。Sammon 映射（又名 Sammon 投影）试图使数据项的低维投影（表示）的成对距离与其原始距离相匹配。因此，我们必须定义算法使用的度量。

度量

假设我们有一个度量空间和两个向量，

vector.PNG

那么距离的通用定义是所谓的闵可夫斯基度量，它定义为

minkowky.PNG

最常用的是欧几里得度量（lambda := 2）

euklidean.PNG

或曼哈顿度量（也称为城市街区度量，lambda := 1）

manhattan.PNG

与欧几里得距离相比，曼哈顿度量在计算上开销较小，因此在本文中，使用了曼哈顿度量。

投影算法

假设有一组有限的向量样本 {xi}，令 dij = d(xi,xj) 为 xi 和 xj 之间的定义距离。令 ri 为 xi 在显示（超）平面上的图像位置。然后，其原理是将位置 ri, i=1,2,...,n 放置在平面上，使得它们的所有相互距离 ||ri - rj|| 尽可能接近输入空间中相应向量的距离。

投影误差

为了量化投影的“好坏”，Sammon 提出了一个在文献中称为 Sammon 应力（Sammon's stress）的成本函数。

sammon_stress.PNG

最小化投影误差

因此，投影旨在最小化该函数，并且投影问题可以看作是一个函数最小化问题，该问题无法以封闭形式求解，只能近似求解。对于这类问题，存在几种（迭代）算法

  • 梯度下降
  • 遗传算法
  • 模拟退火
  • 粒子群优化
  • 其他启发式方法

Sammon [Sam69] 提出了一种陡度下降迭代过程，该过程可以以分量形式表示为

sammons_formula.PNG

其中 (9) 中的 alpha 是所谓的“魔术因子”，并且是完全通过实验找到的，取值为 0.3 到 0.4。尽管这是一个严格的数学推导，但它存在一些缺点。当任何距离变为 0 时，由于除以零，算法会失败。此外，该公式似乎计算量很大。在我进行测试期间，此方法产生的结果并不令我满意。Kohonen [Koh01] 提供了一种效果相对较好且易于实现的启发式方法。显示向量的校正定义如下：

heuristic.PNG

这里 0 < lambda < 1 可以在过程中单调递减到零。为了获得可接受的统计精度，校正次数应为样本数的 10e4 到 10e5 倍。我的测试表明，在大约 10 次迭代后，最终位置就确定了，进一步的迭代是对这些位置的微调。这显然取决于数据集以及 lambda 的衰减，我选择了指数衰减。

实现

对于 Sammon 投影，提供了两个类。第一个计算投影，第二个创建图像以供显示。

Projection

曼哈顿距离

internal static double ManhattenDistance(double[] vec1, double[] vec2)
{
	double distance = 0;

	for (int i = 0; i < vec1.Length; i++)
		distance += Math.Abs(vec1[i] - vec2[i]);

	return distance;
}

Fisher-Yates 洗牌

为了随机选择向量，我经常使用一个需要洗牌的索引数组。洗牌是通过 Fisher-Yates-Shuffle 算法完成的

internal static void FisherYatesShuffle(this T[] array)
{
	for (int i = array.Length - 1; i > 0; i--)
	{
		// Pick random position:
		int pos = _rnd.Next(i + 1);

		// Swap:
		T tmp = array[i];
		array[i] = array[pos];
		array[pos] = tmp;
	}
}

距离矩阵

在算法迭代过程中，输入空间中的距离不会改变，因此这些距离会被预先计算并存储在距离矩阵中。尽管该矩阵是对称的且对角线元素为 0，但仍存储了完整矩阵。一方面，在现代计算机上内存不是大问题，另一方面，“查找”可以这样进行，使得矩阵的元素处于连续顺序，从而比存储为缩减的三角形矩阵所需的两次间接寻址更快。
距离矩阵的元素计算如下：

private double[][] CalculateDistanceMatrix()
{
	double[][] distanceMatrix = new double[this.Count][];
	double[][] inputData = this.InputData;

	for (int i = 0; i < distanceMatrix.Length; i++)
	{
		double[] distances = new double[this.Count];
		distanceMatrix[i] = distances;

		double[] inputI = inputData[i];

		for (int j = 0; j < distances.Length; j++)
		{
			if (j == i)
			{
				distances[j] = 0;
				continue;
			}

			distances[j] = Helper.ManhattenDistance(
				inputI,
				inputData[j]);
		}
	}

	return distanceMatrix;
}

启发式算法

投影算法的核心如下所示：

public void Iterate()
{
	int[] indicesI = _indicesI;
	int[] indicesJ = _indicesJ;
	double[][] distanceMatrix = _distanceMatrix;
	double[][] projection = this.Projection;

	// Shuffle the indices-array for random pick of the points:
	indicesI.FisherYatesShuffle();
	indicesJ.FisherYatesShuffle();

	for (int i = 0; i < indicesI.Length; i++)
	{
		double[] distancesI = distanceMatrix[indicesI[i]];
		double[] projectionI = projection[indicesI[i]];

		for (int j = 0; j < indicesJ.Length; j++)
		{
			if (indicesI[i] == indicesJ[j])
				continue;

			double[] projectionJ = projection[indicesJ[j]];

			double dij = distancesI[indicesJ[j]];
			double Dij = Helper.ManhattenDistance(
					projectionI,
					projectionJ);

			// Avoid division by zero:
			if (Dij == 0)
				Dij = 1e-10;

			double delta = _lambda * (dij - Dij) / Dij;

			for (int k = 0; k < projectionJ.Length; k++)
			{
				double correction =
					delta * (projectionI[k] - projectionJ[k]);

				projectionI[k] += correction;
				projectionJ[k] -= correction;
			}
		}
	}

	// Reduce lambda monotonically:
	ReduceLambda();
}

Image

图像由 GDI+ 创建，投影的点被缩放到结果图像和图的范围内。可以提供每个点的颜色编码和标签，从而实现更“直观”的图像。

public Bitmap CreateImage(
	int width,
	int height,
	string[] labels,
	Color[] colors)
{
	if (labels != null && labels.Length != _sammon.Count)
		throw new ArgumentException();

	if (colors != null && colors.Length != _sammon.Count)
		throw new ArgumentException();
	//-----------------------------------------------------------------
	Bitmap bmp = new Bitmap(width, height);

	double minX = _sammon.Projection.Min(p => p[0]);
	double maxX = _sammon.Projection.Max(p => p[0]);
	double minY = _sammon.Projection.Min(p => p[1]);
	double maxY = _sammon.Projection.Max(p => p[1]);

	double ratioX = (width - 20) / (maxX - minX);
	double ratioY = (height - 20) / (maxY - minY);

	Brush brush = new SolidBrush(Color.Black);
	using (Graphics g = Graphics.FromImage(bmp))
	using (Font font = new Font("Arial", _fontSize))
	using (StringFormat format = new StringFormat())
	{
		g.Clear(_backGroundColor);

		format.Alignment = StringAlignment.Center;

		double[][] projection = _sammon.Projection;
		for (int i = 0; i < projection.Length; i++)
		{
			double[] projectionI = projection[i];
			double x = projectionI[0];
			double y = projectionI[1];

			x = (x - minX) * ratioX + 10;
			y = (y - minY) * ratioY + 10;

			if (colors != null)
			{
				brush.Dispose();
				brush = new SolidBrush(colors[i]);
			}

			g.FillEllipse(
				brush,
				(float)(x - _pointSize / 2d),
				(float)(y - _pointSize / 2d),
				_pointSize,
				_pointSize);

			if (labels != null)
			{
				var size = g.MeasureString(labels[i], font);

				g.DrawString(
					labels[i],
					font,
					brush,
					(float)(x - _pointSize / 2d),
					(float)(y - _pointSize / 2d - size.Height),
					format);
			}
		}
	}

	brush.Dispose();

	return bmp;
}

示例和用法

数据集

提供的示例展示了 Fisher 的著名 鸢尾花数据集 的投影，该数据集可从 UCI 的机器学习存储库获取。
该四维数据集包含 3 个类别，每个类别有 50 个实例，每个类别代表一种鸢尾花。一个类别与其他两个类别是线性可分的；后两者彼此之间不是线性可分的。

下图显示了数据集的散点图，其中第四维用作标记的大小（来源：SOM-Pak，赫尔辛基大学）

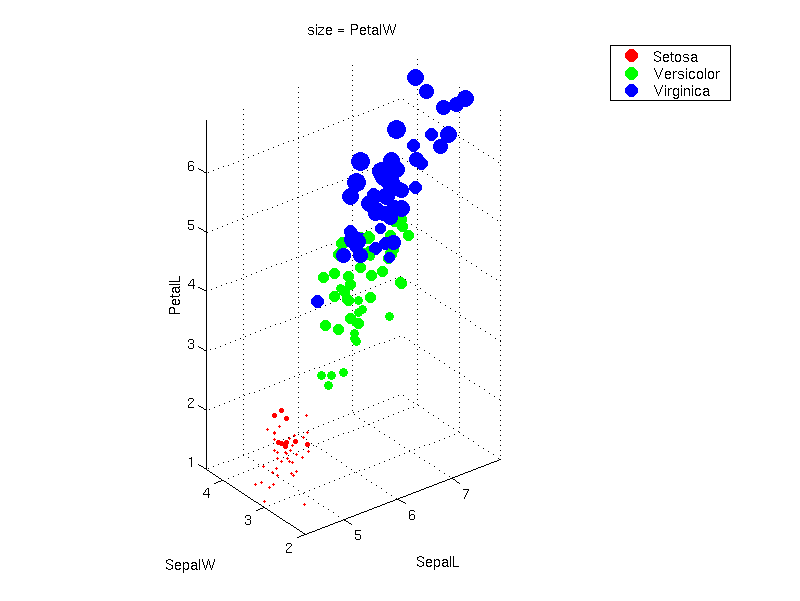
类的用法

用法非常简单。在数据被读入后（在示例中通过 StreamReader 完成），可以计算投影图像

private Bitmap CreateProjection()
{
	SammonsProjection projection = new SammonsProjection(
		_inputData,
		2,
		1000);
	projection.CreateMapping();

	// Create colors and labels - here a lazy version is shown, it should
	// be read from the data set in real applications ;)
	Color[] color = new Color[150];
	string[] labels = new string[150];
	for (int i = 0; i < 50; i++)
	{
		color[i] = Color.Red;
		labels[i] = "set";
	}
	for (int i = 50; i < 100; i++)
	{
		color[i] = Color.Green;
		labels[i] = "vers";
	}
	for (int i = 100; i < 150; i++)
	{
		color[i] = Color.Blue;
		labels[i] = "virg";
	}

	SammonsProjectionPostProcess processing = new SammonsProjectionPostProcess(
		projection);
	processing.PointSize = 4;
	processing.FontSize = 8;
	return processing.CreateImage(300, 300, labels, color);
}

结果

下面是鸢尾花数据集投影的图像：

sammon.png

注意：由于随机初始化，多次运行可能会得到不同的图像。

下面显示了迭代过程中拍摄的一系列图像：

animation_00.png

迭代 0

animation_01.png

 迭代 1

animation_10.png

 迭代 10

可以看到，图像向量的最终位置在第一次迭代中就已获得。注意：图像系列是从与上面显示的最终图像不同的运行中拍摄的。

参考文献

  • [Koh01] T. Kohonen. 自组织映射。Springer，第 3 版，2001 年
  • [Sam69] J. W. Sammon Jr. 用于数据结构分析的非线性映射。IEEE 计算机汇刊，第 C-18 卷，第 5 期，第 401-409 页，1969 年 5 月

历史

  • 2009 年 10 月 20 日：在引言部分添加了额外信息
  • 2009 年 10 月 18 日：初始发布
© . All rights reserved.