65.9K
CodeProject 正在变化。 阅读更多。
Home

NewtonPlus - 快速大数平方根函数

Ryan Scott White
starIconstarIconstarIconstarIconstarIcon

5.00/5 (9投票s)

2022年3月14日

MIT

37分钟阅读

viewsIcon

22551

downloadIcon

227

一个快速、可能是最快的 C# 和 Java 中的大整数和浮点数平方根函数。

目录

引言

下面是一个快速的大整数和浮点数平方根函数。该算法使用多种新旧思想，以比其他算法更高的效率和更好的性能来计算平方根。该函数的性能仅在数字大于 5 x 1014（或 252）时才开始显现。

该算法包含一个核心整数平方根函数和一个用于 BigFloats 的包装器。

  • 整数版本 - 此函数向下舍入到最近的整数（floor）。
  • BigFloats / 实数包装器 – 整数版本的适配器，可添加浮点数和可选的精度。

整数平方根函数已通过各种测试类型和基准测试进行了广泛测试。

C# 版本

性能基准测试

在该算法开发过程中进行了大量基准测试。最初是为了与其他算法进行比较，后来是为了与我自己的版本进行比较。由于性能差异很大，因此使用对数尺度图表进行比较。请注意，微小的差异也意味着巨大的性能差异。已添加一些 Big-O 示例作为 X3、X2 * Log(X) 和 X2 的颜色带。这些带都收敛于 0,0，但已移除图表底部以获得更好的可见性。

A chart showing the performance of the Newton Plus Function as compared to other functions.

对于测试的功能，似乎有四类性能。时间示例来自我的测试工作站，并且会因不同的硬件而略有差异。

  • Big O(cn) – 这些算法对大数运行时间最长。一个 40,000 位二进制数将需要大约 1e6000 年。这些在上面的图表中并未显示。
  • Big O(n3) – 这些算法比 O(cn) 算法快得多。一个 40,000 位二进制数将需要 500 秒。
  • Big O(n2 * log(n)) – 这些是更快速、更周密的算法。一个 40,000 位二进制数大约需要 230 毫秒。
  • Big O(n2) – 该项目与此带宽一致，甚至可能略快。一个 40,000 位二进制数大约需要 8 毫秒。

代码（C# 版本）

直接给我看代码，好吗？

public static BigInteger NewtonPlusSqrt(BigInteger x)
{
    if (x < 144838757784765629)          // 1.448e17 = ~1<<57
    {
        uint vInt = (uint)Math.Sqrt((ulong)x);
        if ((x ≥ 4503599761588224) && ((ulong)vInt * vInt > (ulong)x)) //4.5e15 = ~1<<52
        {
            vInt--;
        }
        return vInt;
    }

    double xAsDub = (double)x;
    if (xAsDub < 8.5e37)   //   8.5e37 is long.max * long.max
    {
        ulong vInt = (ulong)Math.Sqrt(xAsDub);
        BigInteger v = (vInt + ((ulong)(x / vInt))) >> 1;
        return (v * v ≤ x) ? v : v - 1;
    }

    if (xAsDub < 4.3322e127)
    {
        BigInteger v = (BigInteger)Math.Sqrt(xAsDub);
        v = (v + (x / v)) >> 1;
        if (xAsDub > 2e63)
        {
            v = (v + (x / v)) >> 1;
        }
        return (v * v ≤ x) ? v : v - 1;
    }

    int xLen = (int)x.GetBitLength();
    int wantedPrecision = (xLen + 1) / 2;
    int xLenMod = xLen + (xLen & 1) + 1;

    //////// Do the first Sqrt on hardware ////////
    long tempX = (long)(x >> (xLenMod - 63));
    double tempSqrt1 = Math.Sqrt(tempX);
    ulong valLong = (ulong)BitConverter.DoubleToInt64Bits(tempSqrt1) & 0x1fffffffffffffL;
    if (valLong == 0)
    {
        valLong = 1UL << 53;
    }

    ////////  Classic Newton Iterations ////////
    BigInteger val = ((BigInteger)valLong << (53 - 1)) + 
                     (x >> xLenMod - (3 * 53)) / valLong;
    int size = 106;
    for (; size < 256; size <<= 1) {
        val = (val << (size - 1)) + (x >> xLenMod - (3 * size)) / val;  }

    if (xAsDub > 4e254) {                      // 1 << 845
        int numOfNewtonSteps = BitOperations.Log2((uint)(wantedPrecision / size)) + 2;

        //////  Apply Starting Size  ////////
        int wantedSize = (wantedPrecision >> numOfNewtonSteps) + 2;
        int needToShiftBy = size - wantedSize;
        val >>= needToShiftBy;
        size = wantedSize;
        do {
            ////////  Newton Plus Iterations  ////////
            int shiftX = xLenMod - (3 * size);
            BigInteger valSqrd = (val * val) << (size - 1);
            BigInteger valSU = (x >> shiftX) - valSqrd;
            val = (val << size) + (valSU / val);
            size *= 2;
        } while (size < wantedPrecision);
    }

    /////// There are a few extra digits here, lets save them ///////
    int oversidedBy = size - wantedPrecision;
    BigInteger saveDroppedDigitsBI = val & ((BigInteger.One << oversidedBy) - 1);
    int downby = (oversidedBy < 64) ? (oversidedBy >> 2) + 1 : (oversidedBy - 32);
    ulong saveDroppedDigits = (ulong)(saveDroppedDigitsBI >> downby);

    ////////  Shrink result to wanted Precision  ////////
    val >>= oversidedBy;

    ////////  Detect a round-ups  ////////
    if ((saveDroppedDigits == 0) && (val * val > x))
    {
        val--;
    }

    // //////// Error Detection ////////
    // // I believe the above has no errors but to guarantee the following can be added.
    // // If an error is found, please report it.
    // BigInteger tmp = val * val;
    // if (tmp > x)
    // {
    //     throw new Exception("Sqrt function had internal error - value too high");
    // }
    // if ((tmp + 2 * val + 1) ≤ x)
    // {
    //     throw new Exception("Sqrt function had internal error - value too low");
    // }

    return val;
}

浮点版本 / 适配器

通过这个项目，我还想做一个用于大浮点数的 BigFloat 版本。为此，从头开始构建了几个 BigFloat 版本。尽管如此，所需要的只是一个简单的包装函数来处理 BigInteger 版本。 BigFloat 和 BigInteger 版本大致相同。一个封装函数，如下所示，只是为 BigInteger 版本增加了一些“调味品”，以跟踪精度和偏移。

(BigInteger val, int shift) SunsetQuestSqrtFloatUsingIntVersion
                (BigInteger x, int shift = 0, int wantedPrecision = 0)
{
    int xLen = (int)x.GetBitLength();
    if (wantedPrecision == 0) wantedPrecision = xLen;
    if (x == 0) return (0, wantedPrecision);
    int totalLen = shift + xLen;
    var needToShiftInputBy = (2 * wantedPrecision - xLen) - (totalLen & 1);
    var val = SunsetQuestSqrt(x << needToShiftInputBy);
    var retShift = (totalLen + ((totalLen > 0) ? 1 : 0)) / 2 - wantedPrecision;
    return (val, retShift);
}

预/后计算相对简单。简而言之，我们从 Sqrt 函数获得的精度是我们输入精度的一半。因此，如果我们想要 20 位的精度，我们只需将输入 X 的大小缩放到 40 位。

偏移量主要是简单的计算。“(totalLen & 1)”是必需的，以确保我们以偶数位数进行偏移。例如，10000 的二进制平方根是 100。这个结果只是一个偶数右移。如果我们有 Sqrt(0b100000)（即 32），那么 Sqrt 是 0b101（即 5），这不再是简单的右移。我们只需要保持输入长度为奇数。

“(totalLen > 0) ? 1 : 0)”部分是因为我们总是希望通过返回偏移量来向下舍入。

四舍五入到最近整数版本 / 适配器

这里的 Sqrt 函数都向下舍入到最近的整数。这是整数函数的标准。如果平方根函数的结果是 99.999999998，那么它应该向下舍入到 99。但是，在某些情况下，舍入到最近的整数是首选。为此，只需使用标准的整数平方根函数计算一个额外的位数即可。如果额外的位数是“0”，则向下舍入，如果是“1”位，则向上舍入。

所以，类似

BigInteger SqrtNearestInt(BigInteger x)
{
    x <<= 2; // left shift by 2
    var result = SunsetQuestSqrt(x);
    if (result & 1 ==1)
	     result ++;
    return (res >> 1); //right shift by 1
}

注意：此项未经测试。

测试

该算法已进行了广泛测试，我相信所有错误都已消除。但是，为了保证正确性，可以在 sqrt 函数末尾附近添加以下内容。这会带来大约 10% 的性能成本。

// lets test the integer fuction: val = Sqrt(x)
BigInteger squared = val * val;
if (squared > x)
{
    Console.WriteLine($"val^2 ({squared}) < x({x})");
    throw new Exception("Sqrt function had internal error - value too high");
}
if ((squared + 2 * val + 1) ≤ x)
{
    Console.WriteLine($"(val+1)^2({(squared + 2 * val + 1)}) ≥ x({x})");
    throw new Exception("Sqrt function had internal error - value too low");
}

在整数平方根测试上花费了大量时间。它在 32 核 1950x Threadripper 上运行了数天，没有出现任何错误。
测试包括

  • 验证 1：过去数字测试中的常见问题
  • 验证 2：暴力测试（从零开始）[运行到 3.4e11 或 237]
  • 验证 3：2n + [-5 到 +5] 测试
  • 验证 4：n[2 到 7] + [-2 到 2] 测试
  • 验证 5：n2 –[0,1] 测试 – 与验证 4 重叠但测试更大数
  • 验证 6：随机数测试

测试量非常广泛，希望没有错误，但如果发现任何错误，请报告。

注意：Java 的 Sqrt 函数是从 Java 一行一行地转换为 C# 的，但出于某种原因，在 C# 中转换和运行时，最后几位偶尔会出现错误。这可能是某种舍入差异，尚未调查。Java 的 Sqrt（在 Java 中）没有这些错误。

Java 版本

我想创建一个 Java 版本，因为 Java 是最常用的编程语言之一。我基本上采用了 C# 版本并做了一些调整。我的 Java 技能很有限，所以我确信还可以进行更多优化。使用 Norton Plus，对于长度在 64 位到 10240 位之间的数字，它仍然比内置的 Java BigInteger Sqrt 快 15 倍到 45 倍。对于长度小于 64 位的数字，内置的 Java 版本具有优势，因为它可以使用私有的 Java 库。对于长度大于 64 位的数字，Newton Plus 快得多，但是，如果我们使用私有的 Java BigInteger 方法和 MutableBigInteger，那么我们可以获得更高的性能。

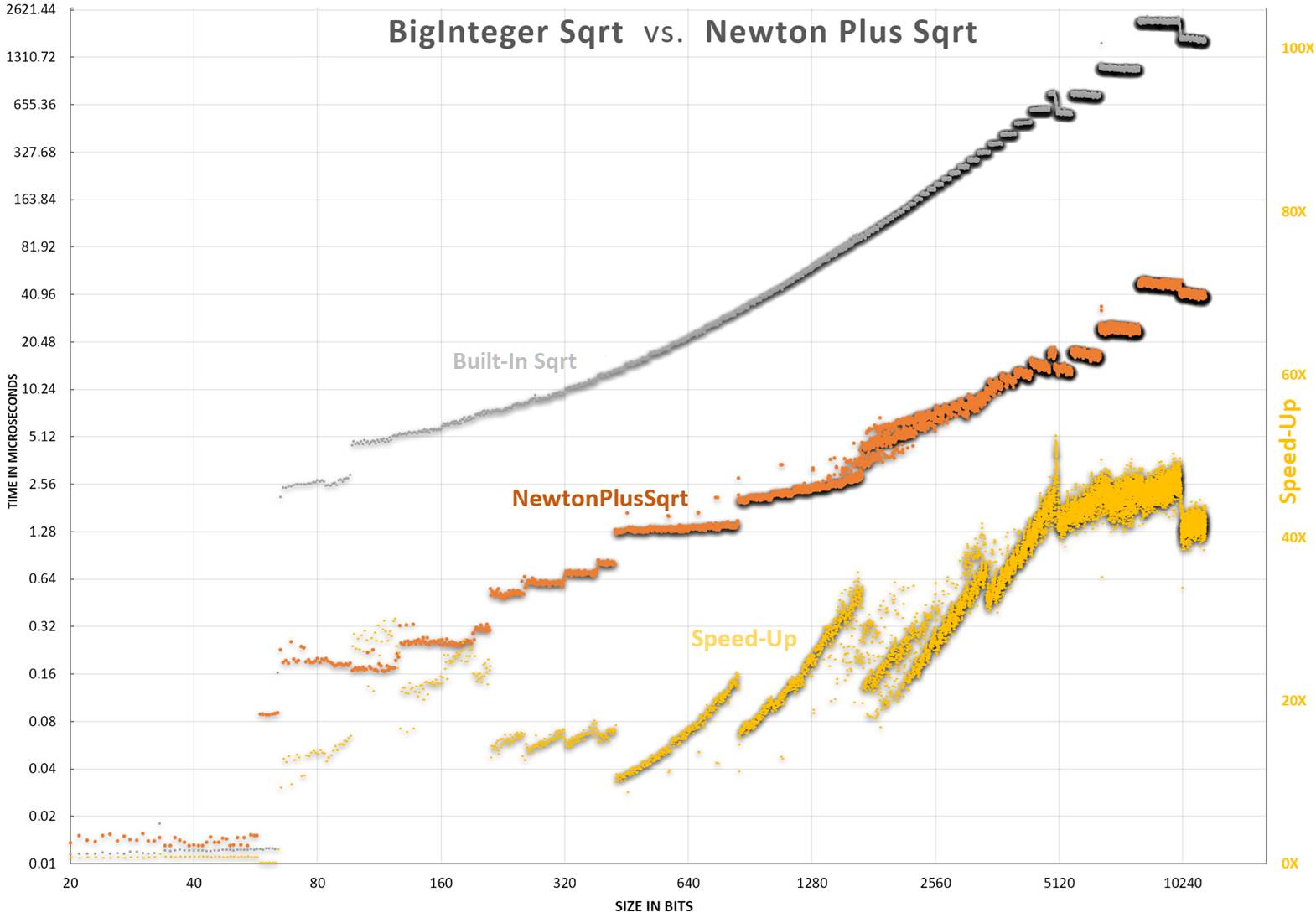
性能图表

下面的点代表不同大小的随机数的平均得分。灰色点是 Java 的 Big Integer 的性能。橙色是本文的 Newton Plus。每个点代表两次试验的平均值，每次试验都是一个包含数千到数百万次测试的循环。

随机说明

  • 黄色是加速比。它只是 NewtonPlus/JavasSqrt。
  • 对于长度约为 10240 位的数字，速度快了 50 倍（5000%）。对于更大的数字，我预计这个数字会更高，就像 C# 图表一样。

下面我们放大垂直方向以获得更好的观看效果。

对数视图提供了最佳的观看效果。我认为这最能显示比较。每条水平线代表 2 倍的性能提升。此处还显示了使用右侧轴的黄色加速比。加速比只是 NewtonPlus 时间除以 Java 版本。

代码（Java 版本）

// A fast square root by Ryan Scott White. 
public static BigInteger NewtonPlusSqrt(BigInteger x) {
  if (x.compareTo(BigInteger.valueOf(144838757784765629L)) < 0) {
    long xAsLong = x.longValue();
    long vInt = (long)Math.sqrt(xAsLong);
    if (vInt * vInt > xAsLong)
      vInt--;
    return BigInteger.valueOf(vInt); }

  double xAsDub = x.doubleValue();
  BigInteger val;
  if (xAsDub < 2.1267e37) // 2.12e37 largest here 
                           // since sqrt(long.max*long.max) > long.max
  {
    long vInt = (long)Math.sqrt(xAsDub);
    val = BigInteger.valueOf
             ((vInt + x.divide(BigInteger.valueOf(vInt)).longValue()) >> 1);
  }
  else if (xAsDub < 4.3322e127) {
    // Convert a double to a BigInteger
    long bits = Double.doubleToLongBits(Math.sqrt(xAsDub));
    int exp = ((int) (bits >> 52) & 0x7ff) - 1075;
    val = BigInteger.valueOf((bits & ((1L << 52)) - 1) | (1L << 52)).shiftLeft(exp);

    val = x.divide(val).add(val).shiftRight(1);
    if (xAsDub > 2e63) {
      val = x.divide(val).add(val).shiftRight(1); }
  }
  else // handle large numbers over 4.3322e127
  {
    int xLen = x.bitLength();
    int wantedPrecision = ((xLen + 1) / 2);
    int xLenMod = xLen + (xLen & 1) + 1;

    //////// Do the first Sqrt on Hardware ////////
    long tempX = x.shiftRight(xLenMod - 63).longValue();
    double tempSqrt1 = Math.sqrt(tempX);
    long valLong = Double.doubleToLongBits(tempSqrt1) & 0x1fffffffffffffL;

    if (valLong == 0)
      valLong = 1L << 53;

    //////// Classic Newton Iterations ////////
    val = BigInteger.valueOf(valLong).shiftLeft(53 - 1)
        .add((x.shiftRight(xLenMod - 
               (3 * 53))).divide(BigInteger.valueOf(valLong)));

    int size = 106;
    for (; size < 256; size <<= 1) {
      val = val.shiftLeft(size - 1).add(x.shiftRight
                 (xLenMod - (3*size)).divide(val));}

    if (xAsDub > 4e254) { // 4e254 = 1<<845.77 
      int numOfNewtonSteps = 31 - 
           Integer.numberOfLeadingZeros(wantedPrecision / size)+1;

      ////// Apply Starting Size ////////
      int wantedSize = (wantedPrecision >> numOfNewtonSteps) + 2;
      int needToShiftBy = size - wantedSize;
      val = val.shiftRight(needToShiftBy);

      size = wantedSize;
      do {
        //////// Newton Plus Iteration ////////
        int shiftX = xLenMod - (3 * size);
        BigInteger valSqrd = val.multiply(val).shiftLeft(size - 1);
        BigInteger valSU = x.shiftRight(shiftX).subtract(valSqrd);
        val = val.shiftLeft(size).add(valSU.divide(val));
        size *= 2;
      } while (size < wantedPrecision);
    }
    val = val.shiftRight(size - wantedPrecision);
  }

  // Detect a round ups. This function can be further optimized - see article.
  // For a ~7% speed bump the following line can be removed but round-ups will occur.
  if (val.multiply(val).compareTo(x) > 0)
    val = val.subtract(BigInteger.ONE);

  // Enabling the below will guarantee an error is stopped for larger numbers.
  // Note: As of this writing, there are no known errors.
  BigInteger tmp = val.multiply(val);
  if (tmp.compareTo(x) > 0) {
    System.out.println("val^2(" + val.multiply(val).toString() 
           + ") ≥ x(" + x.toString()+")"); 
    System.console().readLine();
    //throw new Exception("Sqrt function had internal error - value too high"); 
  }
  if (tmp.add(val.shiftLeft(1)).add(BigInteger.ONE).compareTo(x) ≤ 0) {
    System.out.println("(val+1)^2(" 
           + val.add(BigInteger.ONE).multiply(val.add(BigInteger.ONE)).toString() 
           + ") ≥ x(" + x.toString() + ")"); 
    System.console().readLine();
    //throw new Exception("Sqrt function had internal error - value too low");  
  }

  return val;
}

世界上最快的处理大数的平方根？

Java 和 C# 的世界上最快……我认为是的。但这个项目并不是世界上最快的平方根。

我发现的最快的是 GMP 平方根。它明显快得多。GMP/MPIR 可能更快，因为它用汇编和 C 编写 - 都是低级语言。在编写 asm/c 时，可以充分利用硬件架构，包括 SSE/MXX 128 位指令/寄存器，优化缓存和其他接近金属的技巧/指令。

以下是一些非常粗略的比较：（单位：纳秒）

  GMP 此项目 加速比
1E+77 350 1058 3.0 倍
1E+154 650 2715 4.2 倍
1E+308 1150 5330 4.6 倍
1E+616 1650 7571 4.6 倍
1E+1233 2450 14980 6.1 倍
1E+2466 4250 35041 8.2 倍
1E+4932 6650 121500 18 倍
1E+9864 17650 458488 26 倍
1E+19728 51850 1815669 35 倍
1E+39457 144950 6762354 47 倍

优化

所有这些加速都是通过不同的优化、技巧、技术、创意或我们想怎么称呼它们来实现的。这些想法中的每一个都增加了整体性能。这里的想法来自我自己和他人。

首先，让我们回顾一下基础知识。有几种长期以来已知的求解平方根的方法，最流行的是牛顿法（也称为巴比伦方法或赫罗方法）。其可以概括为

Let x = the number we want to find the sqrt of
Let v = a rough estimate of Sqrt(x)
while(desired_precision_not_met) 
    v = (v + x / v) / 2
return v

当手动计算牛顿法的平方根（以及其他方法）时，我们首先找到最重要的数字。这个第一步可以通过选择一个位数是输入位数一半的数字来完成。因此，数字 2101（一个带有 101 个二进制零的 1）将有一个不错的起点，约为 251。这大致使我们以正确的比例获得一位数的准确性。

然后是牛顿迭代。对于 v = (v + x / v) / 2 的每一次迭代，精度位数都会加倍。初始的 1 位猜测加倍为 2 位精度，然后是 4 位，然后是 8 位，依此类推（注意：为简化起见，省略了移位）。

初始猜测：100000000000000000000000000000000000000000000000000…
v = (v + x / v) / 2 的第一次迭代：110000000000000000000000000000000000000000000000000…
v = (v + x / v) / 2 的第二次迭代：101101010101010101010101010101010101010101010101010…
v = (v + x / v) / 2 的第三次迭代：101101010000010100000101000001010000010100000101000…
v = (v + x / v) / 2 的第四次迭代：101101010000010011110011001100111111101010111110110…
v = (v + x / v) / 2 的第五次迭代：101101010000010011110011001100111111100111011110011…

以二进制形式查看这一点很有帮助——如上面不断增长的下划线正确位数所示。用十进制（base10）表示，这一点将完全隐藏。用二进制进行数学计算有一些见解。

好的，基础知识介绍完毕，现在让我们来探讨不同的优化。我将从更重要的开始，所以至少看看前几个。

优化：缩小除法（Newton Plus）

好吧，让我先介绍我的第一号优化。

在计算牛顿法时，最耗时部分是除法。对于计算机和人类来说，除法都非常耗时。如果能以某种方式缩小这个除法，我们就能在计算工作量方面处于更有利的位置。

手动进行典型的牛顿法二进制计算时，会有一个突出的现象。“v +”只是前面迭代的 v。此外，这些位数已经存在，所以我们只是将上半部分左移 1 位。如果我们已经有了这些位数，我们真的需要在除法中包含它们吗？既然已经有了，我们能否以某种方式去除这部分？答案是它们不需要包含在除法中。这些位数是结果 v 的首位。记住V2中的位数是 x，所以如果我们仅仅去除V，那么在经过平方根计算后，它就像我们刚刚去除了我们试图预先去除的 v。

观察经典牛顿法中“V +”的作用的一种方式是，它只是将X/V的左侧移位一位，基本上是注入一个零。在这个例子中，“V +”将零注入括号内。

 V +   = 1011010100000100000000000000000

 X / V = 1011010100000101111001100110011

 sum:       10110101000001[0]01111001100110011

请注意，“V +”只是将上半部分左移一位。

所以，我们已经有了其中一半的位数，那么为什么要保留它们在除法中？当我们看经典牛顿法时，X / V = 1011010100000101111001100110011。如果我们看X/V部分，它可以分为两部分。我们已经知道的上半部分（粗体）因为它已经存在于当前的V中。所以，我们只需要找到下半部分。

要去除前导 v 位（上半部分），我们可以从分子中的X减去V2。V2的前半部分位数是 x 的高位。所以，我们在平方根计算之前，或者在计算之后，从 x 中减去V。

如果我们预先从 x 中减去V2，看起来是这样的。

     V +  =  10110101000001000000000000000000
(X-V^2)/V =                  1111001100110011
 sum:        10110101000001001111001100110011

或者我们可以不用加法，而是通过连接位来完成。

“V” concatenated with “(X-V^2)/V”
   = 1011010100000100 concatenated with 1111001100110011 
   = 10110101000001001111001100110011

Newton Plus 的代码

下面是 Newton Plus 的一次迭代。应重复此过程直到达到所需的精度。

void NewtonPlus(BigInteger x, int xLenMod, ref int size, ref BigInteger val)
{
    int shiftX = xLenMod - (3 * size);
    BigInteger valSqrd = (val * val) << (size - 1);
    BigInteger valSU = (x >> shiftX) - valSqrd;
    val = (val << size) + (valSU / val);
    size *= 2;
}

参数

  • "X" 是输入。我们要找 Sqrt 的值。
  • "xLenMod" 是 Len(X) 向上舍入到下一个偶数。它只需计算一次。
  • "size" 是 val 的当前维护大小。这样就无需每次调用下面的方法时都重新计算。调用方法时，大小也会加倍。
  • "val" 是当前结果。每次调用此函数都会使精度加倍。

仅供比较，这是一个典型的牛顿法。

void NewtonClassic(BigInteger x, int xLenMod, ref int size, ref BigInteger val)
{
    BigInteger tempX = x >> xLenMod - (3 * size) + 1;
    val = (val << (size - 1)) + tempX / val;
    size <<= 1;
}

最简单的形式看起来是

Vn+1 = (Vupshifted) + (Xdownshifted - V2upshifted) / V

详细来说

XLenMod = IntLog2(X) + (IntLog2(X) mod 2) Vn+1
=(V << (IntLog2(V)+1)) + ([X >> ((XLenMod - 3 * IntLog2(V)) - (V2 << IntLog2(V))] / V)

或者使用连接...

Vn+1=V 连接 ([X >> ((XLenMod - 3 * IntLog2(V)) - (V2 << IntLog2(V))] / V)

注释

  • 为了使连接方法起作用，我们必须精确得到V部分。如果“Xdownshifted - V2upshifted”结果为负数，则不精确且会失败。
  • 此时，“V +”或更准确地说，“(V << (IntLog2(V) + 1)) +”只是将 V 左移并在前面加上，我们可以直接进行连接。移位 V 并将两者相加比简单地连接要复杂得多。

Newton Plus 的一个例子

假设我们要查找 123456789（111010110111100110100010101）的平方根。

我们将从第 3 行（见下表）开始，这里 v 为“101”。（注意：可以通过我们要查找 Sqrt(x) 的数字的二进制长度来估计前几位。如果为偶数，我们从“110”开始；如果为奇数，我们从“101”开始。上面的数字有 27 位，所以我们的初始选择是“101”。）

首先，我们在第 5-7 行执行经典牛顿法步骤。我们在这里使用经典牛顿法，因为它在小数上更快，因为我们有 64 位寄存器，而且在这个例子中，它会加倍以显示经典牛顿法的样子。

然后，在第 8-14 行，完成一次 Newton Plus 迭代。第 8 行是 v 的平方然后左移。

然后，在第 10 行，我们预先从 X 中减去V2。这是神奇的一步。我们减去V2，计算平方根，然后只加回V。

在第 12 行，我们执行典型的除法，但分子比标准牛顿法小。

在第 13 行，我们将 V 左移，然后将其添加到第 14 行的 T 上。不过，有人可能会争辩说，在标准牛顿法中，我们“加 V”，这有什么不同吗？不同之处在于我们正在恢复 V，而标准牛顿法中的“+V”只是将位数的上半部分左移 1 位。

Line     十进制 二进制 长度
1 数字   123456789 111010110111100110100010101 [27]
2          
3 初始选择 V=27（为奇数） 5 101 [3]
4          
5 牛顿法步骤 X 右移 >> 29 11101 [5]
6   X/V 5 101 [3]
7   V=V+↑ 10 1010 [4]
           
8 NewtonPlus 步骤 V2, << 800 1100100000 [10]
9   X 右移 >> 941 1110101101 [10]
10   X-V2 141 10001101 [8]
12   T=(X-V2)/V 14 1110 [4]
13   V 左移 << 160 10100000 [8]
14   V=T+(V<<) 174 10101110 [8]
15 真实答案   173 10101101 [8]
16 误差   1 1 [1]
           
17 NewtonPlus 步骤 V2, << 3875328 1110110010001000000000 [22]
18   X 右移 >> 3858024 1110101101111001101000 [22]
19   X-V2 17304 100001110011000 [15]
20   T=(X-V2)/V 99 01100011 [8]
21   V 左移 << 44544 1010111000000000 [16]
22   V=T+(V<<) 44445 1010110110011101 [16]
23 真实答案   44444 1010110110011100 [16]
24 误差   1 1 [1]
           
25 NewtonPlus 步骤 V2, << 6.47285E+13 1110101101111011001001001001001000000000000000 [46]
26   X 右移 >> 6.47269E+13 1110101101111001101000101010000000000000000000 [46]
27   X-V2 1618771968 1100000011111001000000000000000 [31]
28   T=(X-V2)/V 36421 1000111001000101 [16]
29   V 左移 << 2912747520 10101101100111010000000000000000 [32]
30   V=T+(V<<) 2912711099 10101101100111000111000110111011 [32]
31 真实答案   2912711096 10101101100111000111000110111000 [32]
32 误差   3 11 [2]

这里，它更像数学格式…

或者使用连接...

随机说明

  • 只是输入X的位数长度。
  • 只计算一次。如果X的长度是奇数，则加 1。这个数字应始终为偶数。

进一步增强 Newton Plus

在上面，我们计算了V2的完整答案，但我们实际上只需要计算下半部分。V2的上半部分已存在于 x 中。因此，与其计算完整的V2（在“V2- X”中），我们只需要计算V2的下半部分位数，然后就可以停止了。不过，此时 x 仍然包含这些位数，因此需要将它们移除。我们实际上只需要 x 的中间部分。

计算V2的下半部分，然后减去 x 的一个子集位数将得到新的位数。这些新的附加位数可以附加到我们正在构建的当前 v 上。

我在 C# 中尝试过这一点，但 .NET 的 BigInteger 并不真正允许我们计算 V * V 的下半部分。我尝试过 ModPow()，但性能似乎并不高，因为 ModPow() 正在进行除法，而我只想在计算 V * V 到一半时停止。此外，我的实现有一些错误，并不总是正确的。可能需要构建一个自定义的 BigInteger 类。

void NewtonPlus(BigInteger x, int xLenMod, ref int size, ref BigInteger val)
{
    BigInteger tmp2 = (BigInteger.ModPow(val, 2, BigInteger.One << (size + 1)) << (size));
    BigInteger tmp3 = ((x >> (xLenMod - (3 * size))) & 
                      ((BigInteger.One << (2 * size + 1)) - 1));
    BigInteger valSU2 = tmp3 - tmp2;

    val = (val << (size + 1)) + (valSU2 / val);
    size = (size << 1) + 1;
}

影响：中等

由...使用：无 - 个人想法（“Newton Plus”这个名字只是我assigned 的名字。）

优化：使用一个起始大小，通过重复加倍最终达到正确的精度。

我们计算出一个初始大小，这样如果我们不断加倍它，它最终将达到我们想要的精度。

假设预期结果大小为 600 位，我们得到一个初始免费猜测，具有 64 位的已知精度。如果我们使用牛顿法来不断加倍，我们会得到 128、256、512，然后我们在 579 位进行部分计算。

  64 位内存段用于 BigInteger 存储 时间
初始值 64                   0
牛顿法循环 1 64 128                 2*2=4
牛顿法循环 2 64 128 192 256             4*4=16
牛顿法循环 3 64 128 192 256 320 384 448 512     8*8=64
牛顿法循环 4 64 128 192 256 320 384 448 512 576 640 9*9=81

现在我们可以通过从一个大小开始来改进这一点，这个大小通过不断加倍会得到目标大小或稍大的结果。

  64 位内存段用于 BigInteger 存储 时间
初始值 37                   0
牛顿法循环 1 64 74                 2*2=4
牛顿法循环 2 64 128 148               3*3=9
牛顿法循环 3 64 128 192 256 296           5*5=25
牛顿法循环 4 64 128 192 256 320 384 448 512 576 592 9*9=81

与上一个表相比，每一个空块都节省了一次计算。

这还有进一步改进的空间。从上面的示例表中，我们最终得到了 592 位。这比我们需要的多了 13 位。在上一步，我们比需要的多了 7 位。这是因为我们的初始大小 64 位太小，分辨率不足。相反，我们可以从最大初始值 128 位开始。我们可以通过使用我们最初的 64 位并进行一次牛顿迭代来获得这个值。这次牛顿迭代会非常快，因为它非常小。但现在，如果我们再次使用更大的数字，我们将得到 73 位。（579 -> 290 -> 146 -> 73）当我们用 73 位再次加倍时，我们得到 73 -> 146 -> 292 -> 584。请注意，我们现在只计算了 584 位，而不是之前的 592 位。这更接近我们的目标 579 位。在这个例子中，它并没有加快任何速度，但如果存在“循环 5/6”行，则会消失一些块。

总的来说，目标尺寸越大，初始尺寸应该越大。对于这个算法，我对小数跳过这一点，并在大约 500 位处进行正确的大小调整。

还有另一种方法是多次重新调整。也许每 n 次迭代进行一次正确的大小调整。

高效生成起始大小

为了生成一个起始大小，我们可以从完整大小开始，然后不断减半，直到它足够小以适应初始猜测。579 -> 290 -> 146 -> 74 -> 37。所以，37 将是我们的起始点。类似

int startingSize = expectedOutputSize; 
while (startingSize > 64) { startingSize >>= 1; doublingCt++; }

在这里，startingSize 将包含我们需要的初始大小。在这个例子中，64 位是我们初始猜测的精度。而 doublingCt 是我们需要进行的牛顿迭代次数。

对于大数有效的另一种方法

int doublingCt = BitOperations.Log2((uint)((wantedPrecision – 1) / 64)) + 1;
int startingSize = ((wantedPrecision – 1)>> doublingCt) + 1;

影响：主要（对小于 4e127 的数字没有影响，对更大的数字影响很大）

由...使用：无 - 个人想法

优化：直接使用硬件平方根处理小数

我们可以使用今天大多数处理器都存在的内置硬件平方根函数。双精度浮点平方根函数最多可以处理 53 位有效二进制数字，并给出 26 位精度的输出。

使用内置浮点数，在 C# 中通过 Math.Sqrt(someDouble) 暴露，对于最多 13 位的精度将给出精确答案，并且对于最多 28 位的精度可能会向上舍入。因此，当输入较小时，函数可以尝试直接使用硬件 Sqrt。如果输入超过 53 位，则效果不佳。像 Java 的 BigInteger 平方根函数这样的许多不同的平方根实现都使用过这个技巧。

双精度硬件平方根精度
输入范围（位数） 0-26 26-57
输入范围（数字） 0 – 67108863 67108864 - 2^57
输出精度（位数） 13 位 28.5 位
输出精度（数字） 0 – 8,191 8192 - 379625062
准确性 精确！（始终向下舍入） 向上或向下舍入

影响：主要（仅对小数）

类别：硬件-软件特定（硬件特性）

由...使用：常用 - 我能找到的第一个使用双精度平方根处理小数（小于 double.max）的例子

优化：使用硬件双精度平方根初始化较大数的前 53 位

如果我们要查找一个大于硬件可直接提供的 53 位的较大数的平方根，我们可以将其右移减小尺寸，然后执行硬件平方根，然后左移放大尺寸。这将为我们留下答案，但只有前 53 位。

假设我们要查找 2596139662575945865093856568695112 的平方根。我们的数字有 111 位长...

111111111111111111000111010110001011100110111110011111100111001010101011110010010110001101010100101100101001000

现在这个数字太大，无法放入硬件平方根。所以，让我们将其截断以适合 53 位。我们可以一次去除 2 位（不是 1!!!）。我们需要去除任何 2 的倍数位，因为这本质上就像提取 4、16、64 等。在平方根之前将其提取出来，之后很容易将其放回。所以，如果我们提取五个 2 位对（或右移 10），在执行硬件平方根后，我们只需通过左移 5 位将五个位数加回去。

我们可以通过右移 58 位（29x2）使其成为 53 位来去除右侧...

11111111111111111100011101011000101110011011111001111

然后我们需要将其放入双精度浮点的分数部分，然后执行硬件平方根。输出在双精度的分数位中，将显示如下

11111111111111111110001110101100010110110100111000001

太好了，现在我们有了数字的前 53 位，但我们实际上需要 56 位才能得到整个答案。我们可以通过一次牛顿迭代来获得我们需要的额外精度。使用一次牛顿迭代可以将 53 位加倍到 106 位——足够我们需要的 56 位精度。

对于小数，这可以带来不错的提升，但遗憾的是，对于大数，这种提升变得不那么重要了。此优化无助于 BigO 性能。我们节省了大约五次牛顿迭代，而这些是计算速度最快的迭代。我们基本上为任何较大的平方根函数节省了固定的时间。

在我的 CPU 上，它在计算中节省了大约 0.8 微秒。对于像 1e14 这样的小数字，这是非常显著的（0.85 微秒到 0.05 微秒是 16 倍加速），但是，当数字进入大数范畴时，0.8 微秒就变得无关紧要了。原本需要 1 毫秒的东西，通过这种优化只需要 0.9992 毫秒。Big-O 表示法会忽略这种优化，因为它是一种常数加速。

影响：主要（仅对小数，无 BigO 帮助）

由...使用

优化：使用达到的精度或预先计算的牛顿迭代次数

当手动用二进制计算牛顿法的平方根时，可以很快发现每次迭代都会使精度加倍。可以预先计算迭代次数，或者在答案增长时监控精度。这比检查答案是否正确或是否停止变化要好，因为那些需要更多的计算。

shiftX = xLenMod - (3 * size);
while (size < wantedPrecision) <-----Escape here when desired precision met.
{
   BigInteger topOfX2 = (x >> shiftX);
   BigInteger valSquared4 = (val * val) << (size - 1);
   BigInteger valSU = topOfX2 - valSquared4;
   BigInteger div = valSU / val;
   val = (val << size) + div;
   shiftX -= 3 * size;
   size <<= 1;
}

影响：主要

类别：基础

由...使用：以前未用于整数平方根，但已用于浮点平方根

优化：使用二叉搜索树按比例选择最佳优化

一个二叉树，可以找到处理给定大小输入的最佳方法是很有用的。这几乎是显而易见的，并且对这一点的实际影响很小，但我还是想包括它。

下面的示例显示了 4 层深度…

Text Description automatically generated

影响：次要

优化：在 sqrt 硬件快速结果高达 6.7e7 之前转换为 'long'

这可能是一个 C# 的特性，但将 double 转换为 long 再进行 sqrt 会带来一些额外的性能。

示例

if (xAsDub < 67108864) 
{
    return (int)Math.Sqrt((ulong)xAsDub);
}

这仅适用于小于 67108864 的数字。

影响：小于 257 的数字：主要；大于 257 的数字：无（或轻微负面影响）

类别：硬件-软件特定（编译器/语言特性 - 可能仅适用于 C#）

由...使用：在此项目中，我使用了来自

优化：随着精度增长而增大数据类型（Biginteger）

这个优化几乎是显而易见的，但我还是会把它包括进来。当执行牛顿法时，只花时间计算精度内的位数。我们可以得到一个初始猜测，比如 53 位，所以我们不需要一开始就处理一个容器，其大小是结果的完整大小。只有在最后一步我们才会这样做。

如果一个人直接使用 while(desired_precision_not_met) V = (V + X/V) / 2 执行牛顿法而不进行降位，那么我们进行了大量不必要的计算。这似乎很明显，但在开始时并不清楚。

为了说明这一点，假设我们正在计算一个 600 位数字的平方根。一个朴素的方法是始终处理“X”的全部 600 位。下表显示了在整个过程中处理完整宽度所花费的时间。

  64 位内存段用于 BigInteger 存储 时间
牛顿法循环 1 64 128 192 256 320 384 448 512 576 600 9*9=81
牛顿法循环 2 64 128 192 256 320 384 448 512 576 600 9*9=81
牛顿法循环 3 64 128 192 256 320 384 448 512 576 600 9*9=81
牛顿法循环 4 64 128 192 256 320 384 448 512 576 600 9*9=81
                      204

但是我们不需要计算所有这些。深色阴影区域超出了当前精度范围，因此可以跳过这些计算！

一个更好的解决方案是随着精度的提高而增长计算。当每次迭代中精度内的位数翻倍时，我们也应该增长数字的大小。

  64 位内存段用于 BigInteger 存储 时间
牛顿法循环 1 64 128                 2*2=4
牛顿法循环 2 64 128 192 256             4*4=16
牛顿法循环 3 64 128 192 256 320 384 448 512     8*8=64
牛顿法循环 4 64 128 192 256 320 384 448 512 576 600 9*9=81
                      165

由于较大的数字计算的成本呈指数级增长，因此缩短这些计算会产生重大影响。第一个表显示花费了 204 个单位的时间，而第二个表花费了 165 个单位的时间。

影响：主要（对小于 1e30 的数字没有影响，对更大的数字影响很大）

类别：基础

由...使用：常用（例如：Java 的 BigInteger Sqrt）

优化：一个快速取整方法

如果我们试图找到 15 的平方根，例如，我们的答案是 4，那么在某个地方发生了向上舍入。这在硬件 sqrt 和软件中都很常见。sqrt 的预期行为是向下舍入（floor）结果。所以，在这个例子中，3 是正确的。我们可以通过简单地将我们的答案 4 平方得到 16 来发现这种向上舍入。如果 16 大于我们的 15，那么答案就太高了，需要通过简单的减下来降低。

//// Detect and repair a round-up (i.e. 101010.11111111101)
if (result * result > x)
    result--;

这种方法比进行完整的牛顿迭代并检查结果是否稳定要快得多。它有 3 个操作：（1）乘法（2）与大 x 和 a 的比较（3）减法。

可以进一步优化此方法；我们只需要计算和比较“result * result”和输入“X”的差异所在的小部分。这将在中间部分，然后向右。请参阅下面的进一步优化部分。

影响：次要

类别：基础

由...使用：个人想法 - 然而，后来我注意到其他人也使用了它

优化：将硬件 Sqrt 扩展到 1.45e17，通过向下取整结果

双精度中的硬件 Sqrt() 会产生约 53 位。

if (x < 144838757784765629)    // 1.448e17 = ~1<<57
{
    uint vInt = (uint)Math.Sqrt((ulong)x);
    if ((x ≥ 4503599761588224) && ((ulong)vInt * vInt > (ulong)x))  // 4.5e15 =  ~1<<52
        vInt--;

    return vInt;
}

影响：次要，仅限非常小的数字

类别：软件/硬件特定

由...使用：无 - 个人观察

优化：使用硬件 sqrt 的“+1”处理高达 4e31（已弃用）

注意：此优化已**弃用**，并且不在当前草案中。

如果我们在之前增加 x，结果在 2e16 和 2e31 之间是正确的。

if (xAsDub < 4e31 && xAsDub > 2e16)  
{
    long v = (long)Math.Sqrt(BitConverter.Int64BitsToDouble
            (BitConverter.DoubleToInt64Bits(xAsDub) + 1));
    return (v + (x / v)) >> 1;
}

影响：次要 - 仅在 2e16 到 2e31 的范围内有帮助

类别：硬件-软件特定（浮点数）

由...使用：无 - 实验发现

优化：检查是否比 1 大或小 1（已弃用）

注意：此优化已**弃用**，并且不在当前草案中。

这与之前的某个方法类似，但支持比 1 小的情况。

// The below would test something like 'val = sqrt(x)'
BigInteger valSq = val * val;
if (valSq > x)
    val--;
else if ((valSq + (val << 1) + 1) ≤ x)
    val++;

影响：次要

类别：基础

由...使用:

优化：处理由于最后一次迭代产生的额外位数造成的最终舍入问题。（已弃用）

注意：此优化已**弃用**，并且不在当前草案中。

舍入问题的一个恼人之处在于，会出现可怕的 XXXX.11111111111101 类型的可向上舍入的结果。起初，我保留了一个不断增长的额外位数集，如果这些位数产生 11111111 风格的数字，我会检测并向下舍入。后来，在查看二进制输出后，搜索十进制二进制位数（但跳过最后 BITS_IN_BACK 个零）似乎更好。如果为零，那么我们怀疑有向上舍入。但是，有时这种情况会失败，并且当前导位数有几个 1 时也会发生。（例如 11111111101001…）。在这两种情况下，我们都怀疑有向上舍入。我必须承认这更像是一种猜测，所以如果任何部分有错误，那就是这一部分。

const int BITS_IN_BACK  = 4; // 3-4 (when FRONT==8)
const int BITS_IN_FRONT = 8; // 1-10(when BACK==3)
BigInteger mask = ((BigInteger.One << 
                  (curShift - Size - BITS_IN_BACK)) - 1) << BITS_IN_BACK;
BigInteger remainder = (mask & val);
val >>= curShift - Size;

//// Detect and repair minor round-up   (ie 101010.11111111101)
if (remainder.IsZero
    || ((val >> (exp - BITS_IN_FRONT) == (1 << BITS_IN_FRONT - 1)) 
    && ((x.GetBitLength() % 2) == 1)))
if (val * val > x)
val--;

影响：次要（对小于 4e127 的数字没有影响，对更大的数字影响很大）

来源：无 - 个人想法

进一步的优化思路 - 供世界上的其他人

可能的想法：更快的“val * val”

这个优化前面已经提到过了。

下面的 Newton Plus 计算可能可以改进。

Vn+1 = (Vupshifted) + (Xdownshifted - V2upshifted) / V

在上面，我们计算了V2的完整答案，但我们实际上只需要计算下半部分。V2的上半部分已经存在于X中。因此，与其计算完整的V2（在“V2- X”中），我们只需要计算V2的下半部分位数，然后就可以停止了。不过，此时 x 仍然包含这些位数，因此也需要将它们移除。我们实际上只需要 x 的中间部分。

计算V2的下半部分，然后减去 x 的一个子集位数将得到新的位数。这些新的附加位数可以附加到我们正在构建的当前 v 上。

我在 C# 中尝试过这一点，但内置的 BigInteger 并不真正允许我们计算 v*v 的下半部分。我尝试过 ModPow()，但性能似乎并不高，因为 ModPow 函数正在进行除法，而我只想在计算 v*v 到一半时停止。此外，我的实现有一些错误，并不总是正确的。可能需要构建一个自定义的 BigInteger 类。

void NewtonPlus5(BigInteger x, int xLenMod, ref int size, ref BigInteger val)
{
    BigInteger tmp2 = (BigInteger.ModPow(val, 2, BigInteger.One << (size + 1)) << (size));
    BigInteger tmp3 = ((x >> (xLenMod - (3 * size))) & 
                     ((BigInteger.One << (2 * size + 1)) - 1));
    BigInteger valSU2 = tmp3 - tmp2;

    val = (val << (size + 1)) + (valSU2 / val);
    size = (size << 1) + 1;
}

另一种方法是，我们可以通过在V * V之前移除 v 的顶部 25% 的位数来做到这一点。

影响：中等，快 4% 到 6%（有助于 BigO 角度）

类别：基础

来源：无 - 个人想法

可能的想法：连接“val”和“X/Val”而不是移位和加法

牛顿迭代的基本部分包含两部分：（1）V 的左移版本和 X/V

val = (val << shiftAmt) + tempX / val

但是当观察当前 v 的二进制时，会发现一些突出的地方。（左侧保持不变）

迭代 4：v = (v + x / v) / 2 1011010100000100
迭代 5：v = (v + x / v) / 2 10110101000001001111001100110011

左侧下划线部分来自“val << shiftAmt”，右侧部分是“tempX/val”。所以，我们实际上可以进行连接。左移和加法是不需要完成的工作。我们实际上可以简单地将位连接在一起。

所以，在我的 C# 示例中，我使用了“移位和加法”版本，因为内置的 BigInteger 类不支持连接。但是，通过创建一个具有此属性的自定义 BigInteger 类仍然可以实现这一点。

此外，V 的完整空间可以被预留，以防止不必要的内存复制。我们只需要填充 X/V 部分（下划线位右侧的位），并在迭代中完成。所以我们只需要写一次结果 V！

影响：未知

类别：基础和平台

来源：无 - 个人想法

可能的想法：利用额外的幸运位数

在每次牛顿迭代中，我们有时会意外地获得一些免费的精度，这要归功于幸运的猜测。如果我们看下面的迭代 3，我们碰巧获得了 5 位精度。当发生下一次牛顿迭代时，它会将这些意外翻倍。

也许我们可以检测到这些并利用它们。不过，会有一些开销，所以其有用性可能很小（甚至没有）。为了限制开销，我们可以尝试每 x 次循环检测一次——也许是每 4 或 8 次迭代。

这是一个例子。下划线部分将是保证的精度。红色部分是幸运猜测。迭代 1 没有幸运猜测。迭代 2 有 5 个幸运猜测！迭代 3 有两个幸运猜测（最后两个零）以及前一行的加倍效应（所以 2*5 + 2），依此类推。这是一个更极端的例子以供演示。

初始猜测：100000000000000000000000000000000000000000000000000
迭代 1：v = (v + x / v) / 2 110000000000000000000000000000000000000000000000000
迭代 2：v = (v + x / v) / 2 101101010101010101010101010101010101010101010101010
迭代 3：v = (v + x / v) / 2 101101010000010100000101000001010000010100000101000
迭代 4：v = (v + x / v) / 2 101101010000010011110011001100111111101010111110110
迭代 5：v = (v + x / v) / 2 101101010000010011110011001100111111100111011110011
迭代 6：v = (v + x / v) / 2 101101010000010011110011001100111111100111011110011

我们能得到多少免费的位数？一半的时间，我们碰巧得到 1 位，四分之一的时间，我们得到前 2 位。八分之一的时间 - 3 位，依此类推。所以，½ + ¼ + 1/8 + 1/16 + 1/32.. = 1 位（每行平均，但在后续行中放大）。

在这些幸运猜测之后，下一次牛顿迭代会将这些猜测加倍（然后四倍，依此类推）。如果我的数学是正确的，经过 6 次牛顿迭代，我们将节省 1 + 2+(1) + 4+(2+1) + 8+(4+2+1) + 16+(8+4+2+1) + 32+(16+8+4+2+1) = 1,3,7,15,31,63 = = 平均六次迭代后有 122 位（免费位）。

由于性能提升不大，我没有对此做任何事情。此外，检查这会有开销，可能会使其变差。

影响：小

类别：基础

来源：无 - 个人想法

可能的想法：使用可变大整数（平台性能改进）

使用可变的 BigIntegers 而不是不可修改的、不可变的 BigInteger struct - 仅内部使用。在 C# 中，分配给 BigInteger 的内存无法修改，因此任何修改，即使是简单的递增，都会强制重新分配内存。这种好处在大数字上只会增加，从而带来更好的 Big O 型性能。Java 支持这一点，然而，使用以下结构：X.add(1).divide(2)

影响：中等

类别：硬件-软件特定（编译器/语言特性）

可能的想法：使用 C 语言的本地包装器（平台性能改进）

这个项目可以被翻译成一个 C 函数，它会更快。C 语言通常在进行广泛的预编译器方面具有更好的性能，并且在内存可以直接访问方面限制更少。然后，一个包装器可以向其他更高级的语言公开 C 函数。由于 C 包装器本地调用会有一些开销，因此仅对大数字使用它是有意义的……也许 SqrtForReallyBigInts() 只能是本地的。但是，本地包装器函数更具问题，并且便携性较差。

影响：次要

类别：硬件-软件特定（编译器/语言特性）

这个函数是如何产生的？

我需要一个 Big Integer 平方根函数来完成我正在进行的一个项目。我四处看了看，找到了一些，并选择了一个我喜欢的。我喜欢的那个不在我常用的一个网站 StackOverflow 上，所以我就重新发布了它（注明了作者/日期）。过了一段时间，MaxKlaxx 发表了一篇文章。MaxKlaxx 发布了比较他的算法和几个其他算法的基准测试，包括我重新发布的“SunsetQuest” - 即使它不是我的。Sunsetquest 的性能最低，如果有人对我了解很多，我注重高效代码 - 显而易见！所以，我决定自己做一个平方根函数，看看我是否能取得领先。

Max 的算法对于大小整数都很快，对于小数使用内置的硬件 SQRT()，并且对于大数结合牛顿迭代作为初始猜测。

经过几周的零星工作，我放弃了，并写道：“这个项目是个灾难!!!!! 1/8/2021”。但是，过了一段时间，想法开始冒出来。第一个想法基本上是尝试将平方根分解成更小的平方根。长话短说，那个想法是个失败！但是，出于某种原因，想法还在不断涌现，通常是在深夜。下一个想法是预先计算牛顿迭代的步数，而不是等待它稳定下来。下一个想法是启动一个初始大小，这样当我们使用牛顿法不断加倍位宽时，我们最终只会得到所需的大小。最后，还有一个想法是将牛顿法改变为使每个除法步骤更小——我将其命名为 Newton Plus——尽管事后看来，也许它应该称为 Newton Minus，因为我们预先减去了一些数字。让我们说我们正在添加一个负数。

所有这些共同作用，平方根变得超级快。这个解决方案比我能找到的下一个最快的 C# 算法快 43 倍。起初，我试图创造比其他人更快的东西，但过了一段时间，我只是在与自己竞争。

历史

  • 2022 年 3 月 14 日：初始版本
  • 2023 年 7 月 1 日：我注意到 HTML 交换了“<=”和“>=”！！！我敢肯定这造成了混乱。幸运的是，CodeProject 下载和 GitHub 代码文件没有这个问题。我还进行了一些其他 HTML 修复、一般清理/语法，并使示例更容易理解。
© . All rights reserved.